题目描述
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab", p = ".*" 输出:true 解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
解题思路
我们用 f[i]表示 s 的前 i 个字符与 p 中的前 j 个字符是否能够匹配。在进行状态转移时,我们考虑 p 的第 j 个字符的匹配情况:
1)如果 p 的第 j 个字符是一个小写字母,那么我们必须在 s 中匹配一个相同的小写字母,即

也就是说,如果 s 的第 iii 个字符与 p 的第 j 个字符不相同,那么无法进行匹配;否则我们可以匹配两个字符串的最后一个字符,完整的匹配结果取决于两个字符串前面的部分。
2)如果 p 的第 j 个字符是 *,那么就表示我们可以对 p 的第 j−1个字符匹配任意自然数次。在匹配 0 次的情况下,我们有
f[i][j]=f[i][j−2]
也就是我们「浪费」了一个字符 * 星号的组合,没有匹配任何 s 中的字符。
在匹配 1,2,3,⋯ 次的情况下,类似地我们有
f[i][j]=f[i−1][j−2], if s[i]=p[j−1]
f[i][j]=f[i−2][j−2], if s[i−1]=s[i]=p[j−1]
f[i][j]=f[i−3][j−2], if s[i−2]=s[i−1]=s[i]=p[j−1]
⋯⋯
如果我们通过这种方法进行转移,那么我们就需要枚举这个组合到底匹配了 s 中的几个字符,会增导致时间复杂度增加,并且代码编写起来十分麻烦。我们不妨换个角度考虑这个问题:字母 星号的组合在匹配的过程中,本质上只会有两种情况:
匹配 s 末尾的一个字符,将该字符扔掉,而该组合还可以继续进行匹配;
不匹配字符,将该组合扔掉,不再进行匹配。
如果按照这个角度进行思考,我们可以写出很精巧的状态转移方程:
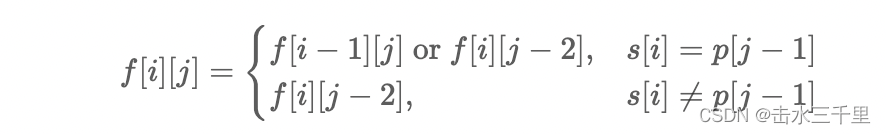
3)在任意情况下,只要 p[j] 是 . ,那么 p[j] 一定成功匹配 s 中的任意一个小写字母。
4)动态规划的边界条件为 f[0][0]=true ,即两个空字符串是可以匹配的
代码实现
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
f[i][j] = f[i][j - 2];
if (matches(s, p, i, j - 1)) {
f[i][j] = f[i][j] || f[i - 1][j];
}
} else {
if (matches(s, p, i, j)) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
/***
*用于判断i, j - 1 或则 i, j的字符是否匹配
*/
public boolean matches(String s, String p, int i, int j) {
if (i == 0) {
return false;
}
if (p.charAt(j - 1) == '.') {
return true;
}
return s.charAt(i - 1) == p.charAt(j - 1);
}
}