1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由 n(n >= 0)个有限节点组成的一个具有层次关系的集合。
那么为什么叫 "树" 呢? (节点也可以称结点,建议称结点,和结构体对上)
我们之所以把它成为 "树",是因为它很像我们现实生活中的树。只是它是倒过来的,根朝上叶子朝下。
① 树有一个特殊的节点,成为根节点,根节点不存在前驱节点。
② 除根节点外,其余节点被分成 M(M>0) 个互不相交的集合 T1、T2、……、Tm,
其中每一个集合 Ti(1 <= i <= m) 又是一颗结构于树类似的字数。
每颗子树的节点有且只有一个前驱,可以有0个或多个后继。
③ 因此,树是递归定义的。因为任何树都会被分成根和子树。

1.2树的相关概念

节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B
的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节
点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
( 有些书上规定根节点的层数为0,这样空树就是-1了,所以若没有特殊说明默认规定根节点的层数为 1)
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是
一个森林)
注意:树型结构中,子树之间不能有交集,否则就不是树形结构。

1.3树的表示
以前学单链表时只有一个指针,双链表两个指针,但是树有多少个指针是不确定的,
因为树没有规定一个节点最多有多少个孩子。那我们该如何定义结构呢?
法一:假设说明了树的度为N,才能勉强用
struct TreeNode
{
int data;
struct TreeNode* sub[N]; // 指针数组
};问题点:
① 可能会存在不少的空间浪费。
② 万一没有限定树的度为多少呢?
法二:vector(C++中这里可以用 vector,但是C里没有)
// 假设我们定义了一个顺序表
typedef int STLDataType; //顺序表的数据类型
typedef struct TreeNode* SLDataType; // 顺序表中存节点的指针
struct TreeNode //SeqList
{
STLDataType data;
SeqList s; // s为SLDataType* array;
};即使你没有告诉我度是多少,我有多少个孩子我就存多少个孩子,所以这里不需要关心度的问题。
但是这里 s 的结构相对复杂,s 里面有一个类型为SLDataType* 的数组,
这个数组已经是二级指针了,SLDataType 展开后又是一个 struct TreeNode* 。
法三:双亲表示法

struct TreeNode
{
int parenti;
int data;
};[ A -1] [ B0 ] [ C0 ] [ D0 ] ...... [ H 3 ]
每一个元素中存的是结构体 struct TreeNode arr[10]
每个元素内只存自己的值和父亲的下标
(A没有父亲是-1,B的父亲下标是0…… H的父亲是D下标为3),可以通过一个值找到自己父亲。
上列的方式各有优缺点,那么有没有最优的方法?
当然有,它就是:左孩子右兄弟表示法
typedef int DataType;
struct Node
{
struct Node* _leftChind1; // 永远指向第一个孩子
struct Node* _rightBrother; // 指向孩子右边的兄弟
DataType _data;
};
解读:无论你有多少个孩子,它都只存两个指针。一个指针永远指向第一个孩子,
另一个指针指向孩子右边的兄弟(亲兄弟)。这个树的度无论为多少,也不需要用顺序表存,
但是你任何一个节点有多少个孩子都能给你表示出来,通过第一个孩子把所有孩子都找出来。
不复杂也没有浪费,只用两个指针就把链接关系都表示出来了,这就是(古人)的智慧。
1.4树在实际中的运用
文件系统的目录树结构、网络拓扑,最短路径问题,搜索引擎、思维导图等

2.二叉树概念及结构

1.1二叉树的概念
定义:二叉树既然叫二叉树,顾名思义即度最大为2的树称为二叉树。
它的度可以为 1 也可以为 0,但是度最大为 2 。
一颗二叉树是节点的一个有限集合,该集合:
① 由一个根节点加上两颗被称为左子树和右子树的二叉树组成
② 或者为空

观察上图我们可以得出如下结论:
① 二叉树不存在度大于 2 的节点,换言之二叉树最多也只能有两个孩子。
② 二叉树的子树有左右之分,分别为左孩子和右孩子。次序不可颠倒,因此二叉树是有序树。
注意:对于任意的二叉树都是由以下几种情况复合而成的:

1.2 满二叉树

定义:一个二叉树,如果每一层的节点数都达到了最大值(均为2),则这个二叉树就可以被称作为 "满二叉树" 。
换言之,如果一个二叉树的层数为h ,且节点总数是 2^h-1,则他就是一个满二叉树。
层数为N的计算公式:


十亿个节点,满二叉树是多少层?
≈ 10亿多
1.3完全二叉树

定义:对于深度为h的,有 n个结点的二叉树,当且仅当其每一个结点都与深度为h的满二叉树中编号从 1 至 n的结点一一对应时称之为完全二叉树。
前h-1层是满的,最后一层不满,但是最后一层从左到右是连续的。
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
所以,满二叉树是一种特殊的完全二叉树(每一层节点均为2)。
常识:
① 完全二叉树中,度为 1 的最多只有 1 个。
② 高度为 的完全二叉树节点范围是

1.4二叉树的性质
四点规则:
① 若规定根节点的层数为 1 ,则一颗非空二叉树的第i层上最多有2^(i-1)个节点。
② 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
③ 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2+1
④ 若规定根节点的层数为1,具有N个结点的满二叉树的深度,h=LogN+1(log以2为底)。
二叉树性质相关选择题:
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A. 不存在这样的二叉树
B. 200
C. 198
D. 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A. n
B. n+1
C. n-1
D. n/2
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A. 11
B. 10
C. 8
D. 12
4. 一个具有767个节点的完全二叉树,其叶子节点个数为()
A. 383
B. 384
C. 385
D. 386
答案解析:
1. n0=n2+1
2.假设叶子节点有X个 则度为0的节点有x-1个,完全二叉树中度为1的节点为0个或1个
所以X+(X-1)+0或1=2n,所以叶子结点x个数为n
3.具有N个结点的满二叉树的深度,h=LogN+1(log以2为底)。
4.同2 .X+(X-1)+0或1=767 x=384
1.B
2.A
3.B
4.A
1.5二叉树的顺序存储:
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树
会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲
解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

完全二叉树的顺序存储中
若父亲下标是i,则左孩子下标是2*i+1 右孩子下标是2*i+2
若孩子下标是i,则父亲下标是(i-1)/2
像上面左图中C下标为2,左孩子F下标就为2*2+1=3,右孩子G下标为2*2+2=6
D下标为3,E下标为4 则父亲B下标为(3-1)/2=1
1.6二叉树的链式存储:
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的
方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩
子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都
是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。

// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* pLeft; // 指向当前节点左孩子
struct BinTreeNode* pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* pParent; // 指向当前节点的双亲
struct BinTreeNode* pLeft; // 指向当前节点左孩子
struct BinTreeNode* pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}3.堆的概念及结构
【百度百科】堆(Heap)是计算机科学中一类特殊的数据结构的统称。
堆通常是一个可以被看做 一棵完全二叉树的数组对象。
完全二叉树的性质就是堆的性质,堆是完全二叉树的顺序结构存储。
① 堆总是一棵完全二叉树。
② 堆中的某个节点的值总是不大于或不小于其父节点的值。
堆的物理结构其实是数组,逻辑结构则是二叉树。
堆的调整算法有多种,其中典型的是:大堆 和 小堆。
3.1小堆:
任意一个节点的两个子节点都比自己的值大或相等,也就是根最小,整个二叉树从上到下递增。
即父亲位,比孩子位,要小;

3.2大堆:
任意一个节点的两个子节点都比自己的值小或相等,也就是根最大,整个二叉树从上到下递减。
即父亲位,比孩子位,要大。

常考选择题:
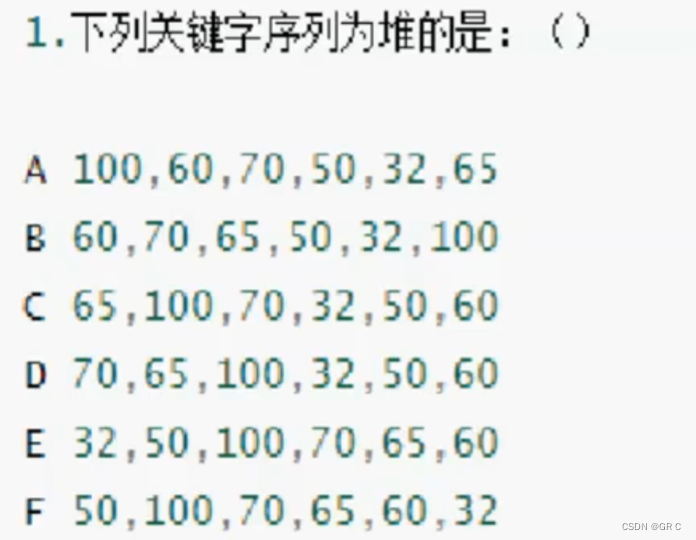
解析:
题目只说明是堆,大堆小堆都可以。
一个个分析后发现除了A都不是
A差不多是这样:
100
60 70
50 32 65
3.3堆的作用
① 堆排序
② 解决TopK问题,在N个数中找出最大的前K个或找出最小的K个......
本篇完。
下一篇我们用代码实现一个大堆。