来源0x3f：https://space.bilibili.com/206214

文章目录

二叉树
- [104. 二叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-binary-tree/)
- [111. 二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)
- [129. 求根节点到叶节点数字之和](https://leetcode.cn/problems/sum-root-to-leaf-numbers/)
二叉树变体（判断相同、平衡、对称）
- [100. 相同的树](https://leetcode.cn/problems/same-tree/)
- [101. 对称二叉树](https://leetcode.cn/problems/symmetric-tree/)
- [110. 平衡二叉树](https://leetcode.cn/problems/balanced-binary-tree/)
- [199. 二叉树的右视图](https://leetcode.cn/problems/binary-tree-right-side-view/)
- [226. 翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/)
二叉搜索树相关(中序遍历二叉搜索树等于遍历有序数组)
- [98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/)
- [230. 二叉搜索树中第K小的元素](https://leetcode.cn/problems/kth-smallest-element-in-a-bst/)
- [501. 二叉搜索树中的众数](https://leetcode.cn/problems/find-mode-in-binary-search-tree/)
- - 暴力（List转int数组：list.stream().mapToInt(Integer::intValue).toArray();）
  - 利用二叉搜索树的性质一次遍历
- [530. 二叉搜索树的最小绝对差](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/)
- [700. 二叉搜索树中的搜索](https://leetcode.cn/problems/search-in-a-binary-search-tree/)
二叉树的最近公共祖先相关
- [236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
- [235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/)
二叉树的层序遍历（BFS）
- [102. 二叉树的层序遍历](https://leetcode.cn/problems/binary-tree-level-order-traversal/)
- [103. 二叉树的锯齿形层序遍历](https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/)
- [513. 找树左下角的值](https://leetcode.cn/problems/find-bottom-left-tree-value/)

二叉树

104. 二叉树的最大深度

难度简单1507

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left, right) + 1;
    }
}

111. 二叉树的最小深度

难度简单928

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

class Solution {
    int res = Integer.MAX_VALUE;
    public int minDepth(TreeNode root) {
        if(root == null) return 0;
        dfs(root,0);
        return res;
    }

    public void dfs(TreeNode node, int depth){
        if(node.left == null && node.right == null){
            res = Math.min(res, depth+1);
            return;
        }
        if(node.left != null) dfs(node.left, depth+1);
        if(node.right != null) dfs(node.right, depth+1);
        return;
    }
}

129. 求根节点到叶节点数字之和

难度中等609

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

class Solution {
    int res = 0;
    public int sumNumbers(TreeNode root) {
        dfs(root, 0);
        return res;
    }

    public void dfs(TreeNode node, int num){
        if(node.left == null && node.right == null){
            res += num * 10 + node.val;
            return;
        }
        if(node.left != null) dfs(node.left, num * 10 + node.val);
        if(node.right != null) dfs(node.right, num * 10 + node.val);
        return;
    }
}

二叉树变体（判断相同、平衡、对称）

100. 相同的树

难度简单967

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

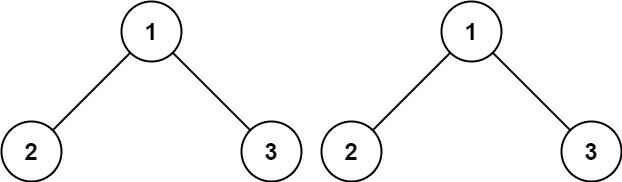
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

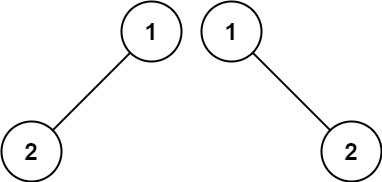
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

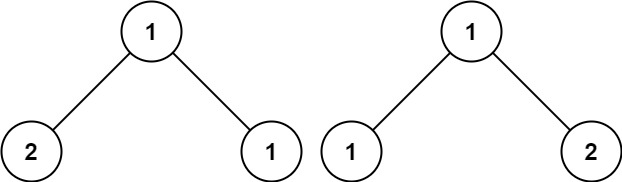
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

class Solution {
    boolean same = true;
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q == null) return true;
        else if(p == null && q != null) return false;
        else if(p != null && q == null) return false;
        else{
            return (p.val == q.val) && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
        }
    }
}

101. 对称二叉树

难度简单2278

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null) return true;
        return iscopy(root.left, root.right);
    }

    public boolean iscopy(TreeNode node1, TreeNode node2){
        if(node1 == null && node2 == null)
            return true;
        if(node1 == null || node2 == null) 
            return false;
        return node1.val == node2.val 
                && iscopy(node1.left, node2.right)
                && iscopy(node1.right, node2.left);
    }
}

110. 平衡二叉树

难度简单1245

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        return get_height(root) > 0 ? true : false;
    }

    public int get_height(TreeNode node){
        if(node == null) return 0;
        int leftheight = get_height(node.left);
        if(leftheight == -1) return -1;
        int rightheight = get_height(node.right);
        if(rightheight == -1) return -1;
        if(Math.abs(leftheight - rightheight) > 1) return -1;
        return Math.max(leftheight, rightheight) + 1;
    }
}

199. 二叉树的右视图

难度中等814

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> rightSideView(TreeNode root) {
        dfs(root, 0);
        return res;
    }

    public void dfs(TreeNode node, int depth){
        if(node == null) return;
        if(depth == res.size()){
            res.add(node.val);
        }
        dfs(node.right, depth+1);
        dfs(node.left, depth+1);
        return;
    }
}

226. 翻转二叉树

难度简单1505

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) return root;
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        root.right = invertTree(root.right);
        root.left = invertTree(root.left);
        return root;
    }
}

二叉搜索树相关(中序遍历二叉搜索树等于遍历有序数组)

中序遍历二叉搜索树等于遍历有序数组

98. 验证二叉搜索树

难度中等1894

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

法一：前序遍历（额外传递判断范围）

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    public boolean isBST(TreeNode node, long left, long right){
        if(node == null) return true;
        long x = node.val;
        boolean valid = (left < x) && (x < right);
        return valid && isBST(node.left, left, x) && isBST(node.right, x, right);
    }
}

法二：中序遍历（从小到大的顺序，即判断是否大于前一个结点值）

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root == null) return true;
        if(!isValidBST(root.left)) return false;
        if(root.val <= pre) return false;
        pre = root.val;
        return isValidBST(root.right);
    }
}

法三：后序遍历（返回最大和最小值，然后最后判断当前节点是否合法）

class Solution {
    public boolean isValidBST(TreeNode root) {
        return dfs(root)[1] != Long.MAX_VALUE;
    }

    public long[] dfs(TreeNode node){
        if(node == null) return new long[]{Long.MAX_VALUE, Long.MIN_VALUE};
        long[] left = dfs(node.left);
        long[] right = dfs(node.right);
        long x = node.val;
        // 小于等于左边最大值 或者 大于等于右边最小值 ： 都是不合法的
        if(x <= left[1] || x >= right[0]){
            return new long[]{Long.MIN_VALUE, Long.MAX_VALUE};
        }
        // 返回左边最小值和右边最大值
        return new long[]{Math.min(left[0], x), Math.max(right[1], x)};
    }
}

230. 二叉搜索树中第K小的元素

难度中等706

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

树中的节点数为 n 。
1 <= k <= n <= 104
0 <= Node.val <= 104

**进阶：**如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

法一：树的遍历+排序

class Solution {
    //先对二叉树进行一次完整遍历，将所有节点存入列表中，最后对列表排序后返回目标值
    List<Integer> list = new ArrayList<>();
    public int kthSmallest(TreeNode root, int k) {
        dfs(root);
        Collections.sort(list);
        return list.get(k-1);
    }

    public void dfs(TreeNode root){
        if(root == null){
            return;
        }
        list.add(root.val);
        dfs(root.left);
        dfs(root.right);
    }
}

法二：树的遍历+优先队列

第K小的元素用大根堆

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b-a);
        Deque<TreeNode> dq = new ArrayDeque<>();
        dq.addLast(root);
        while(!dq.isEmpty()){
            TreeNode node = dq.pollFirst();
            if(pq.size() < k){
                pq.add(node.val);
            }else if(pq.peek() > node.val){
                pq.poll();
                pq.add(node.val);
            }
            if(node.left != null) dq.addLast(node.left);
            if(node.right != null) dq.addLast(node.right);
        }
        return pq.peek();
    }
}

法三：中序遍历

上述两种节点，都没有利用该树为二叉搜索树的特性。

而我们知道，二叉搜索树的中序遍历是有序的，因此我们只需要对二叉搜索树执行中序遍历，并返回第 k 小的值即可。

class Solution {
    int k, res = 0;
    public int kthSmallest(TreeNode root, int _k) {
        k = _k;
        dfs(root);
        return res;
    }

    public void dfs(TreeNode root){
        if(root == null || k <= 0) return;
        dfs(root.left);
        if(--k == 0) res = root.val;
        dfs(root.right);
    }
}

501. 二叉搜索树中的众数

难度简单588

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

输入：root = [1,null,2,2]
输出：[2]

示例 2：

输入：root = [0]
输出：[0]

提示：

树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

**进阶：**你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

暴力（List转int数组：list.stream().mapToInt(Integer::intValue).toArray();）

class Solution {
    Map<Integer, Integer> map = new HashMap<>();
    int max = -1; 
    public int[] findMode(TreeNode root) {
        dfs(root);
        List<Integer> list = new ArrayList<>();
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){
            if(entry.getValue() == max)
                list.add(entry.getKey());
        }
        return list.stream().mapToInt(Integer::intValue).toArray();
    }

    public void dfs(TreeNode node){
        if(node == null) return;
        int x = node.val;
        map.put(x, map.getOrDefault(x, 0) + 1);
        max = Math.max(max, map.get(x));
        dfs(node.left);
        dfs(node.right);
        return;
    }
}

利用二叉搜索树的性质一次遍历

思路：二叉搜索树的中序遍历是一个升序序列，逐个比对当前结点(root)值与前驱结点（pre)值。更新当前节点值出现次数(curTimes)及最大出现次数(maxTimes)，更新规则：若curTimes=maxTimes,将root->val添加到结果向量(res)中；若curTimes>maxTimes,清空res,将root->val添加到res,并更新maxTimes为curTimes。

class Solution {
    int pre = Integer.MIN_VALUE;
    int maxcnt = 0, curcnt = 0;
    List<Integer> res;
    public int[] findMode(TreeNode root) {
        res = new ArrayList<>();
        dfs(root);
        return res.stream().mapToInt(Integer::intValue).toArray();
    }
    // 二叉搜索树中序遍历是递增顺序
    public void dfs(TreeNode root){
        if(root == null) return;
        dfs(root.left);
        //判断当前值与上一个值的关系, 更新 curcnt 和 pre
        if(pre == root.val){
            curcnt++;
        }else{
            pre = root.val;
            curcnt = 1;
        }
        //判断当前数量与最大数量的关系, 更新 list 和 maxTimes
        if(curcnt == maxcnt){
            res.add(root.val);
        }else{ 
            if(curcnt > maxcnt){
                res = new ArrayList<>();
                maxcnt = curcnt;
                res.add(root.val);
            }
        }
        dfs(root.right);
    } 
}

530. 二叉搜索树的最小绝对差

难度简单433

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

输入：root = [4,2,6,1,3]
输出：1

示例 2：

输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

class Solution {
    int pre = (int)-1e5;
    int res = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        dfs(root);
        return res == Integer.MAX_VALUE ? -1 : res;
    }

    public void dfs(TreeNode node){
        if(node == null) return;
        dfs(node.left);
        res = Math.min(res, node.val - pre);
        pre = node.val;
        dfs(node.right);
    }
}

700. 二叉搜索树中的搜索

难度简单365

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

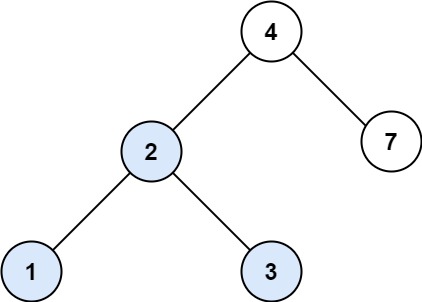
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

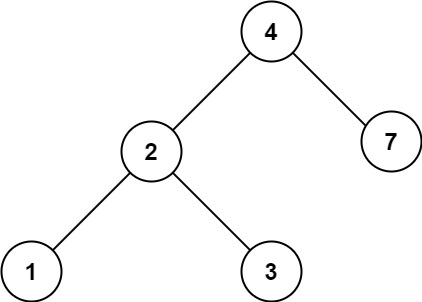
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root == null) return root;
        if(root.val == val) return root;
        else if(root.val > val) return searchBST(root.left, val);
        else return searchBST(root.right, val);
    }
}

二叉树的最近公共祖先相关

236. 二叉树的最近公共祖先

难度中等2153

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q){
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left != null && right != null){
            return root;
        }
        if(left != null) 
            return left;
        else 
            return right;
    }
}

235. 二叉搜索树的最近公共祖先

难度中等1022

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p.val > q.val) return lowestCommonAncestor(root, q, p);
        if(root.val >= p.val && root.val <= q.val) return root;
        else if(root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        else return lowestCommonAncestor(root.right, p, q);
    }
}

二叉树的层序遍历（BFS）

102. 二叉树的层序遍历

难度中等1580

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            while(size-- > 0){
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            res.add(list);
        }
        return res;
    }
}

103. 二叉树的锯齿形层序遍历

难度中等737

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        boolean even = false;
        queue.add(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            while(size-- > 0){
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            if(even) Collections.reverse(list);
            even = !even;
            res.add(list);
        }
        return res;
    }
}

513. 找树左下角的值

难度中等437

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

输入: root = [2,1,3]
输出: 1

示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1

记录遍历的节点，从右往左遍历每层，最后一个出队列的节点就是答案

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        TreeNode node = new TreeNode(-1);
        while(!queue.isEmpty()){
            int size = queue.size();
            while(size-- > 0){
                node = queue.poll();
                if(node.right != null) queue.add(node.right);
                if(node.left != null) queue.add(node.left);
            }
        }
        return node.val;
    }
}