服务端开发Java之备战秋招面试篇1

在这个面试造火箭工作拧螺丝的时代背景下，感觉不是很好，不过还好也是拿到了还行的offer，准备去实习了，接下来就是边实习边准备秋招了，这半年把（技术栈+八股文面经+算法题+项目）吃透，希望等到秋招可以顺利一点，冲吧。

1.MySQL主从复制实现过程及原理？

2.JVM原理？

3.docker常用命令？

4.Spring自带的线程创建方式？

5.Hashmap的添加、查询、删除原理，扩容原理等？

6.MyBatis-plus级联查询？

7.微服务的优点？springBoot的优点？

8.redis崩了可能是哪些问题？

9.MySQL的可重复读的原理？

10.红黑树的原理？二叉树的遍历的时间复杂度？

11.算法题：连续子数组的最大和

12.算法题：链表中环的入口节点

1.MySQL主从复制实现过程及原理？

MySQL主从复制是MySQL自带的功能，无需借助第三方的工具，它是一个异步复制过程，底层是基于MySQL数据库自带的二进制日志功能，就是多台从库(slave)从一台主库(master)进行日志复制，然后进行日志解析并应用到自身，最终实现从库的主库的一致性，常见的主从同步架构有一主多从、双主多从。

一主多从架构：

一般是主库负责所有读写请求，而从库只负责容灾恢复和冗余备份。

如果做了读写分离的话，主库负责写请求，从库负责读请求，可以提升数据库性能。

双主多从架构：

一般是主库1负责所有读写请求，主库2不对外提供服务，只用来容灾恢复。

相比一主多从架构，双主多从架构可以减少宕机时间，更快恢复数据库可用状态。

二进制日志(BinLog)记录了所有的数据操作语句和数据定义语句，该日志对于灾难情况出现后的数据恢复起到至关重要的作用，MySQL的主从复制，就是通过该BinLog实现的。默认MySQL是未开启该日志的。

MySQL主从复制主要分为如下三步，及主从同步原理如下：

第一，主库master将数据变更写入BinLog。

第二，从库slave的IO线程将主库的BinLog拷贝到从库的中继日志(relay log)。

第三，从库SQL线程读取Relay Log文件内容，重新执行SQL语句，将数据更新到他的数据上。

MySQL主从复制的优点？

读写分离，提升数据库性能。
容灾恢复，主服务器不可用时，从服务器提供服务，提高可用性。
冗余备份，主服务器数据损坏丢失，从服务器保留备份。

主从同步延迟问题？主从同步延迟的原因有哪些？主从同步延迟的解决方案？

主从同步最常遇到的问题就是主从同步延迟，可以通过在从库上执行show slave status命令查看延迟时间，Seconds_Behind_Master表示延迟的秒数。

延迟原因：
1）从库性能差，在主库进行读写操作。

2）从库的压力相对较大，读的操作多于写的操作。

3）网络延迟，从库去拷贝主库的BinLog的时候发生网络延迟。

4）当主库有大的事务，当主库有大事务，从库进行拷贝BinLog的时候执行时间较长。

主从同步延迟的解决方案：

1)把从库换成跟主库同等规格的机器。

2)多搞几台从库，分担读请求压力。

3)联系运维或者云服务提供商解决.

4)把大事务分割成小事务执行，大事务不但会产生从库延迟，还可能产生死锁，降低数据库并发性能，所以尽量少用大事务。

如何提升主从同步性能?

1)从库开启多线程复制

在主从同步的最后两步使用多线程，修改配置 slave_parallel_workers=4，代表开启4个复制线程。

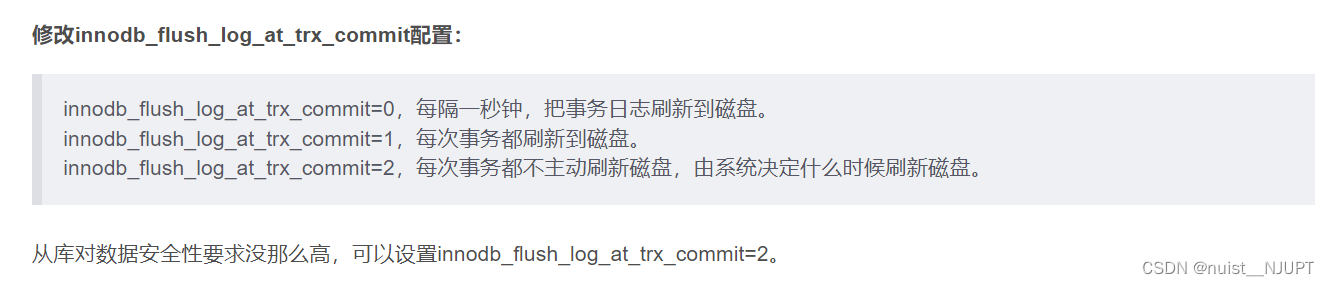
2)修改同步模式，改为异步，如果对数据安全性要求没那么高，可以把同步模式改成半同步复制或者异步复制。

主从同步共有三种复制方式：

全同步复制

当主库执行完一个事务，并且所有从库都执行完该事务后，才给客户端返回成功。

半同步复制

至少有一个从库执行完成后，就给客户端返回成功。

异步复制

主库执行完后，立即返回成功，不关心从库是否执行完成。

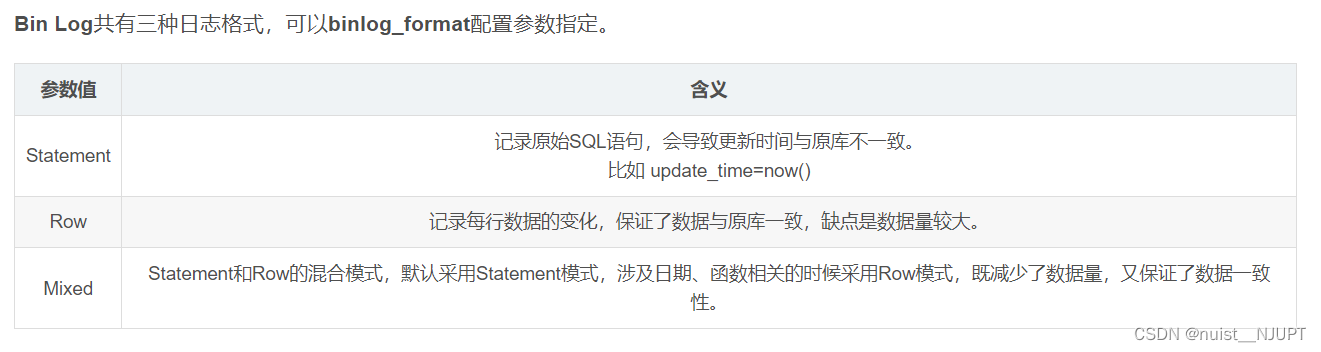
3)修改从库Bin Log配置

2.JVM原理？

我的总结：

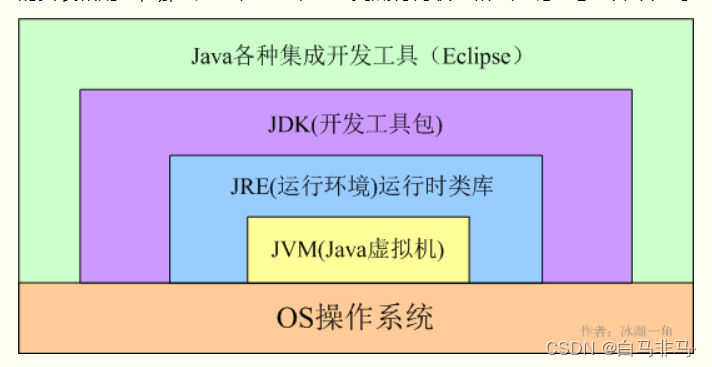
JVM即Java虚拟机，java编译器编译生成字节码文件给JVM。通过JVM将每一条指令翻译成不同平台机器码，通过特定平台运行。JVM的声明周期：诞生->运行->消亡。

JVM的内存结构包括五大区域：程序计数器、虚拟机栈、本地方法栈、堆区、方法区。

参考这篇：JVM原理-超详细总结_伟呀呀呀呀的博客-CSDN博客_jvm原理

3.docker常用命令？

docker常用命令主要包括，基础命令，镜像命令，容器命令，运维命令等，具体可以参考这篇博文：docker 常用命令大全_保护我方胖虎的博客-CSDN博客_docker常用命令

SpringCloud之微服务实用篇3-docker_nuist__NJUPT的博客-CSDN博客

4.Spring自带的线程创建方式？

使用springboot自带@Async注解创建异步线程，为了让@Async注解能够生效，还需要在Spring Boot的主程序中配置@EnableAsync。

Java中有三种常见的线程常见方式以及线程池的创建方式。

5.Hashmap的添加、查询、删除原理，扩容原理等？

HashMap的数据结构：JDK1.7及以前：链表+数组 JDK1.8：数组+链表+红黑树

我们常见的有数据结构有三种结构：1、数组结构 2、链表结构 3、哈希表结构。我们来看看各自的数据结构的特点：数组结构：存储区间连续、内存占用严重、空间复杂度大。存储区间离散、占用内存宽松、空间复杂度小。结合数组结构和链表结构的优点，从而实现了查询和修改效率高，插入和删除效率也高的一种数据结构。

HashMap中的put()和get()和rmove()的实现原理：

map.put(k,v)实现原理：
（1）首先将k,v封装到Node对象当中（节点）。
（2）然后它的底层会调用K的hashCode()方法得出hash值。
（3）通过哈希表函数/哈希算法，将hash值转换成数组的下标，下标位置上如果没有任何元素，就把Node添加到这个位置上。如果说下标对应的位置上有链表。链表上每个节点的k进行equal。如果所有的equals方法返回都是false，那么这个新的节点将被添此时，就会拿着k和加到链表的末尾。如其中有一个equals返回了true，那么这个节点的value将会被覆盖。

map.get(k)实现原理：
(1)先调用k的hashCode()方法得出哈希值，并通过哈希算法转换成数组的下标。
(2)通过上一步哈希算法转换成数组的下标之后，在通过数组下标快速定位到某个位置上。如果这个位置上什么都没有，则返回null。如果这个位置上有单向链表，那么它就会拿着K和单向链表上的每一个节点的K进行equals，如果所有equals方法都返回false，则get方法返回null。如果其中一个节点的K和参数K进行equals返回true，那么此时该节点的value就是我们要找的value了，get方法最终返回这个要找的value。
map.remove(k)实现原理：

1）先调用k的hashCode()方法得出哈希值，并通过哈希算法转换成数组的下标。

2）确定了数组下标位置，查找到要删除的节点，链表的删除比较简单，但是红黑树的删除较为麻烦，涉及到树的再平衡问题。

相比 jdk1.7 的 HashMap 而言，jdk1.8最重要的就是引入了红黑树的设计，当hash表的单一链表长度超过 8 个的时候，链表结构就会转为红黑树结构。

为什么要这样设计呢？好处就是避免在最极端的情况下链表变得很长很长，在查询的时候，效率会非常慢。

红黑树查询：其访问性能近似于折半查找，时间复杂度 O(logn)；
链表查询：这种情况下，需要遍历全部元素才行，时间复杂度 O(n)；

红黑树是一种近似平衡的二叉查找树，其主要的优点就是“平衡“，即左右子树高度几乎一致，以此来防止树退化为链表，通过这种方式来保障查找的时间复杂度为 log(n)。

HashMap的扩容原理：

扩容机制核心方法Node<K,V>[] resize()
HashMap扩容可以分为三种情况：

JDK1.7和JDK1.8的扩容原理不同，参照这篇博客：HashMap之扩容原理_hashmap扩容_Mr_yeml的博客-CSDN博客

6.MyBatis-plus级联查询？

一对一，一对多，和多对多的级联查询，在mybatis中在XML文件中写SQL语句进行查询，查询结果用resultMap进行封装。

在MP中进行级联查询的话，主要借助resultMap定义级联查询，在实体类上注解属性指定resultMap的id，添加级联表映射类的对象属性，来完成的。这样在调用Mybatis公共服务接口、公共映射器接口，返回对象时，自动完成级联查询，体现了MybatisPlus编码高效的优势。

7.微服务的优点？springBoot的优点？

微服务的优点：

1、易于开发和维护

由于微服务单个模块就相当于一个项目，开发这个模块我们就只需关心这个模块的逻辑即可，代码量和逻辑复杂度都会降低，从而易于开发和维护。

2、启动较快

这是相对单个微服务来讲的，相比于启动单体架构的整个项目，启动某个模块的服务速度明显是要快很多的。

3、局部修改容易部署

在开发中发现了一个问题，如果是单体架构的话，我们就需要重新发布并启动整个项目，非常耗时间，但是微服务则不同，哪个模块出现了bug我们只需要解决那个模块的bug就可以了，解决完bug之后，我们只需要重启这个模块的服务即可，部署相对简单，不必重启整个项目从而大大节约时间。

4、技术栈不受限

比如订单微服务和电影微服务原来都是用java写的，现在我们想把电影微服务改成nodeJs技术，这是完全可以的，而且由于所关注的只是电影的逻辑而已，因此技术更换的成本也就会少很多。

5、按需伸缩

我们上面说了单体架构在想扩展某个模块的性能时不得不考虑到其它模块的性能会不会受影响，对于我们微服务来讲，完全不是问题，电影模块通过什么方式来提升性能不必考虑其它模块的情况。

缺点：运维和部署的复杂性。

8.redis崩了可能是哪些问题？

本质就是缓存穿透，缓存雪崩，缓存击穿。

Redis中的缓存穿透、雪崩、击穿的原因以及解决方案（详解）_redis的雪崩和击穿_PeakXYH的博客-CSDN博客

9.MySQL的可重复读的原理？

使用MVCC(多版本并发控制)。

10.红黑树的原理？二叉树的遍历的时间复杂度？

我们先看一下红黑树，JDK1.8在hashMap中加入红黑树，防止链表太长，造成查询性能差的问题。我们先看一下二叉树，排序二叉树和平衡二叉树。

二叉树指的是每个节点最多只能有两个字数的有序树。通常左边的子树称为左子树 ，右边的子树称为右子树 。这里说的有序树强调的是二叉树的左子树和右子树的次序不能随意颠倒。

所谓排序二叉树，顾名思义，排序二叉树是有顺序的，它是一种特殊结构的二叉树，我们可以对树中所有节点进行排序和检索。

若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若她的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
具有递归性，排序二叉树的左子树、右子树也是排序二叉树。

排序二叉树的左子树上所有节点的值小于根节点的值，右子树上所有节点的值大于根节点的值，当我们插入一组元素正好是有序的时候，这时会让排序二叉树退化成链表。

为了解决排序二叉树在特殊情况下会退化成链表的问题（链表的检索效率是 O(n) 相对正常二叉树来说要差不少），所以有人发明了平衡二叉树和红黑树类似的平衡树。

平衡二叉数又被称为 AVL 树，AVL 树的名字来源于它的发明作者 G.M. Adelson-Velsky 和 E.M. Landis，取自两人名字的首字母。

官方定义：它或者是一颗空树，或者具有以下性质的排序二叉树：它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

两个条件：

平衡二叉树必须是排序二叉树，也就是说平衡二叉树他的左子树所有节点的值必须小于根节点的值，它的右子树上所有节点的值必须大于它的根节点的值。
左子树和右子树的深度之差的绝对值不超过1。

其实红黑树和上面的平衡二叉树类似，本质上都是为了解决排序二叉树在极端情况下退化成链表导致检索效率大大降低的问题，红黑树最早是由 Rudolf Bayer 于 1972 年发明的。

红黑树首先肯定是一个排序二叉树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是 RED 或 BLACK 。红黑树有下面5个特性。

性质1：每个节点要么是红色，要么是黑色。
性质2：根节点永远是黑色的。
性质3：所有的叶子节点都是空节点（即null），并且是黑色的。
性质4：每个红色节点的两个子节点都是黑色。（从每个叶子到根的路径上不会有两个连续的红色节点。）
性质5：从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。

红黑树在最差情况下，最长的路径都不会比最短的路径长出两倍。其实红黑树并不是真正的平衡二叉树，它只能保证大致是平衡的，因为红黑树的高度不会无限增高，在实际应用用，红黑树的统计性能要高于平衡二叉树，但极端性能略差。

红黑树参考这篇就可以：红黑树与平衡二叉树_百图详解红黑树_小吴先森的博客-CSDN博客

前序，中序，后序遍历：时间复杂度O(n)，空间复杂度O(n)（递归本身占用stack空间或者用户自定义的stack）
DFS，BFS：时间复杂度O(n)，空间复杂度O(n)（递归本身占用stack空间或者用户自定义的stack）
在最坏情况下，当二叉树中每个节点只有一个孩子节点时，递归的层数为 N，此时空间复杂度为 O(N)。在最好情况下，当二叉树为平衡二叉树时，它的高度为 log⁡(N)，此时空间复杂度为 O(log⁡(N))。

11.算法题：连续子数组的最大和

题目链接：连续子数组的最大和_牛客题霸_牛客网

贪心的思路，不需要额外开辟数组，直接一层循环遍历，之前累加的值累加到当前，比当前大，就即继续累加，否则，从当前开始继续累加，累加过程中找出一个最大值就可以了。

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
       //最好保证时间复杂度为O(n),空间复杂度为O(1)
       int sum = array[0] ;
       int max = array[0] ;
       for(int i=1; i<array.length; i++){
        if(sum + array[i] > array[i]){
            sum += array[i] ;
        }else{
            sum = array[i] ;
        }
          max = sum > max ? sum : max ;
       }
       return max ;
       
    }
}

12.算法题：链表中环的入口节点

题目链接：链表中环的入口结点_牛客题霸_牛客网

使用快慢指针的方法，定义一个快指针，一个慢指针，快指针一次走两步，慢指针一次走一步，两个指针第一次相遇的地方，距离出口的位置和从其实节点到出口的位置距离相同。

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead) {
      ListNode fast = pHead ;
      ListNode slow = pHead ;
      if(fast == null || fast.next == null || fast.next.next == null){
        return null ; //无环
      }
      while(fast != null ){
        slow = slow.next ;
        fast = fast.next.next ;
        if(slow == fast){
            break ;
        }
      }
      if(fast == null){
        return null ;
      }
      fast = pHead ;
      while(slow != fast){ 
        slow =slow.next ; 
        fast = fast.next ;
      }
      return fast ;

    }
}