---

这是CVPR2021的一篇文章, 是利用SOT的一些思想来进行MOT的运动估计.
文章地址: 文章

代码地址: 代码

---

0. 摘要

本文提出了一个孪生(Siamese)式的MOT网络, 该网络用来估计帧间目标的运动. 为了探究运动估计对多目标跟踪的影响, 本文提出了两种运动建模方式: 显式和隐式. 本文在一些数据集上取得了良好的结果.

1. 整体思路

这篇文章是用SOT的思想做MOT的比较好的例子.

整个工作的具体思路是: 利用Siamese网络来更好地预测运动, 而不是Kalman滤波, 相当于用Siamese网络代替了Kalman.

例如, 对于第$t$帧, 我们有第$i$个目标的位置$R_i^t$, 然后我们扩张搜索区域, 在第$t+\delta$帧将$R_i^t$的区域扩展, 初步决定搜索区域为$S_i^{t+1}$, 如下图橙色框所示. 我们的目的是用Siamese网络更好地从$S_i^{t+1}$中估计出目标在下一帧更精确的位置, 进而与检测更好地匹配.

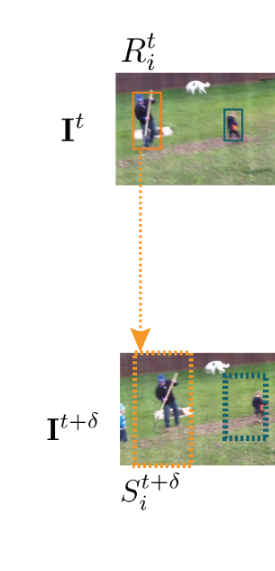
为此, 我们提取$R_i^t$的特征$f_{R_i}^t$和$S_i^{t+1}$的特征$f_{S_i}^{t+\delta }$, 输入至网络中, 输出缩小的可能的新区域${\tilde{R}}_i^{t+\delta }$和该区域中包含目标的可能性$v_i$, 因此整体的模型建模为:

$$v_i,{\tilde{R}}_i^{t+\delta }=\mathcal{T}(f_{R_i}^t,f_{S_i}^{t+\delta },\Theta )$$

其中$\Theta$为网络参数.

上式建模的方式有两种, 一是隐式运动建模, 二是显式运动建模.

1.1 隐式运动建模:

隐式运动建模很简单, 将$f_{R_i}^t$和$f_{S_i}^{t+\delta }$拼接起来输入到MLP, 同时预测置信度和位置. 位置描述的是$t$时刻与$t+\delta$时刻的位置差异, 表示为:

$$m_i=[\frac{x_i^{t+\delta }-x_i^t}{x_i^t},\frac{y_i^{t+\delta }-y_i^t}{y_i^t},\log \frac{w_i^{t+\delta }}{w_i^t},\log \frac{h_i^{t+\delta }}{h_i^t}]$$

因此可以反解出新的位置${\tilde{R}}_i^{t+\delta }=[x_i^{t+\delta },y_i^{t+\delta },w_i^{t+\delta },h_i^{t+\delta }]$

损失函数:

损失函数由两部分组成, 一是目标置信度的focal loss, 二是预测边界框的准确程度. 对于GT框, 我们可以按照$m_i$的式子求出对应的$m_i^{\ast }$ , 定义为:

$$L=l_{focal}(v_i^{\ast },v_i)+\mathbb{I}(v_i^{\ast })l_{reg}(m_i,m_i^{\ast })$$

其中上标$\ast$表示真值, $l_{reg}$表示平滑L1损失.

1.2 显式运动建模

还可以采用更复杂的形式. 采用通道维的互相关操作, 可以通过预测热度图的方式计算像素级的响应图, 有点类似于求解光流. 对于第$t$帧的区域特征$f_{R_i}^t$和第$t+\delta$帧的初步搜索区域特征$f_{S_i}^{t+\delta }$, 计算通道维互相关, 即$r_i=f_{R_i}^t\ast f_{S_i}^{t+\delta }$, 其中$\ast$表示互相关操作, 这样就得到了两种特征图的相似度.

我们利用得到的$r_i$, 进一步预测像素级置信度的map $v$和位置的map $p$, 如下图所示.

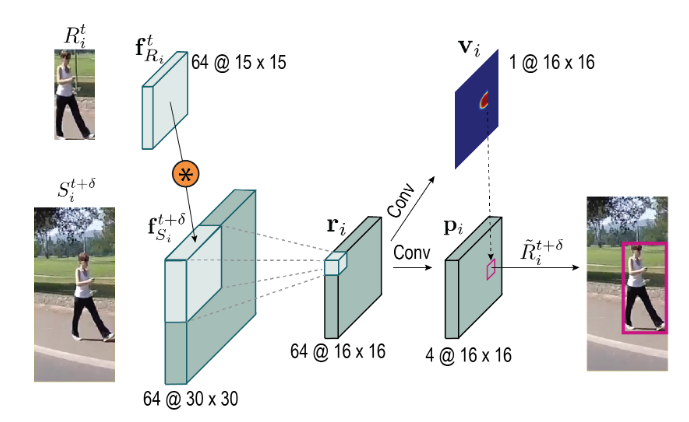
注意这里位置的map和一些无锚检测器类似, 预测的是offset. 具体地, 预测的是真实的bbox与当前像素四个方向的offset. 为此, 我们可以以像素级的置信度相应map中最大的点为准, 找到位置map中对应的位置, 即可直接求解出预测的位置. 也就是:

$$\begin{gathered} {\tilde{R}}_i^{t+\delta }=\mathcal{R}(p_i^{\ast }(x,y));v_i^{t+\delta }=v_i(x^{\ast },y^{\ast }) \\ s.t.(x^{\ast },y^{\ast })=\arg \underset{x,y}{\max }(v_i\ast {\eta }_i) \end{gathered}$$

其中${\eta }_i$为:

$${\eta }_i(x,y)=\lambda \mathcal{C}+(1-\lambda )\mathcal{S}(\mathcal{R}(p(x,y)),R_i^t)$$

表示的是一个penalty map, 其中$\mathcal{C}$是以过去帧位置$R_i^t$的几何中心为中心的cos窗函数, $\mathcal{S}$是预测出的位置和原本位置高宽差异的高斯函数, ${\eta }_i$的作用是为了防止bbox尺寸的突然变化.

损失函数:

与隐式建模类似, 损失函数也是由置信度损失和bbox位置损失组成, 所不同的是该部分预测的是逐像素map, 因此需要逐像素进行计算. 置信度损失仍为focal loss, 位置损失包括中心点的差异与回归损失, 如下式所示:

$$\begin{gathered} L=\sum _{x,y}{l}_{focal}(v_i(x,y),v_i^{\ast }(x,y))+ \\ \sum _{x,y}\mathbb{I}[v_i^{\ast }(x,y)=1](w(x,y)\cdot l_{reg}(p_i(x,y),p_i^{\ast }(x,y))) \end{gathered}$$

$w(x,y)$就是中心点差异.

1.3 训练和推理

训练是按照端到端的方式训练的, 将Faster RCNN的检测损失与上面的损失结合. 推理也比较普通, 就是利用推理出的${\tilde{R}}_i^{t+\delta }$和检测器检测的$R_i^{t+\delta }$简单进行匹配即可.

整体流程下图所示:

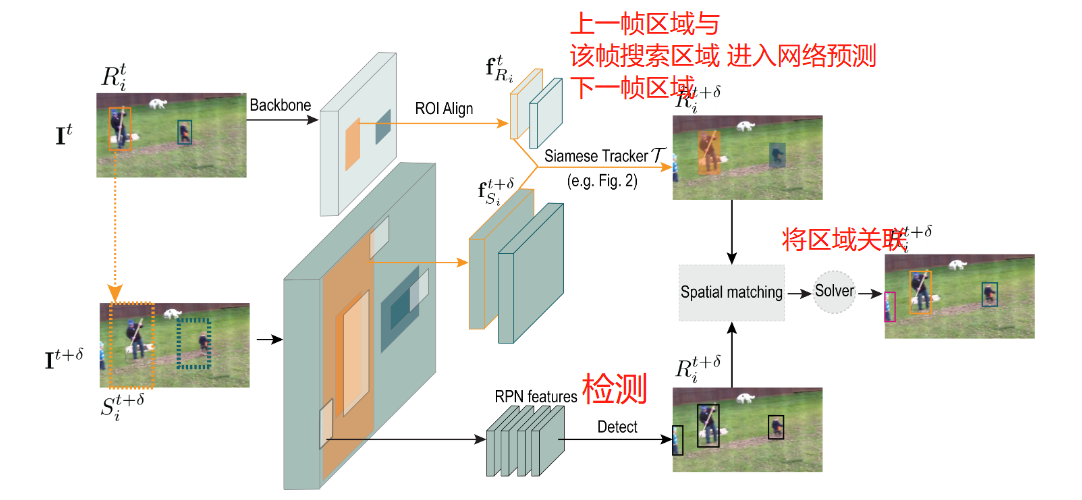
2. 评价

这篇是很简单的一个笔记, 在SOT+MOT的方法里, 这篇应该也算简洁的, 创新之处在于隐式建模反推位置那一块, 以及逐像素map的思想也值得学习.