一、题目描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？

示例 1：

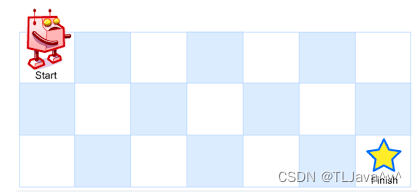
输入：m = 3, n = 7

输出：28

示例 2：

输入：m = 3, n = 2

输出：3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下

2. 向下 -> 向下 -> 向右

3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3

输出：28

示例 4：

输入：m = 3, n = 3

输出：6

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/unique-paths

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二、运行结果

优化空间后内存击败92%。

三、解题思路

冬天规划中比较典型的题目，创建一个m行n列的数组，由于只能向下或向右走（也就是不允许回头），先将数组的第一行和第一列初始化为1（只有一跳路径可以到达），然后 计算数组中剩下的每一个位置的只，每个位置可以从上一个位置或左边一个位置到达，所以状态转移方程为：

dp[i][j] = dp[i-1][j] + dp[i][j-1];

计算完数组中每个位置的值后，dp[m-1][n-1]中的值就是到达该位置的路径数。

四、AC代码

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i=0; i<m; i++)  //初始化第一列
            dp[i][0] = 1;
        for(int j=1; j<n; j++)  //初始化第一行
            dp[0][j] = 1;
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];  //状态转移方程
            }
        }
        return dp[m-1][n-1];
    }
}

优化空间后的代码：

class Solution {
    public int uniquePaths(int m, int n) {
        if(m == 1 || n == 1) return 1;
        int[] dp = new int[n];  //只需要一行
        for(int i=0; i<n; i++)
            dp[i] = 1;
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[j] += dp[j-1];  //状态转移方程
            }
        }
        return dp[n-1];
    }
}