摘要
1140. 石子游戏 II
877. 石子游戏
1406. 石子游戏 III
375. 猜数字大小 II
464. 我能赢吗
486. 预测赢家
1025. 除数博弈
一、动态规划解析
Alice一开始有两个选择:拿前一堆/前两堆石子。如果 Alice 拿前一堆,那么轮到 Bob 时,他也可以在剩下的四堆石子中,拿前一堆/前两堆石子。如果 Bob 拿前一堆,那么又轮到 Alice,不断这样思考下去,可以画出如下搜索树。注意如果可以全部拿完,就全拿。
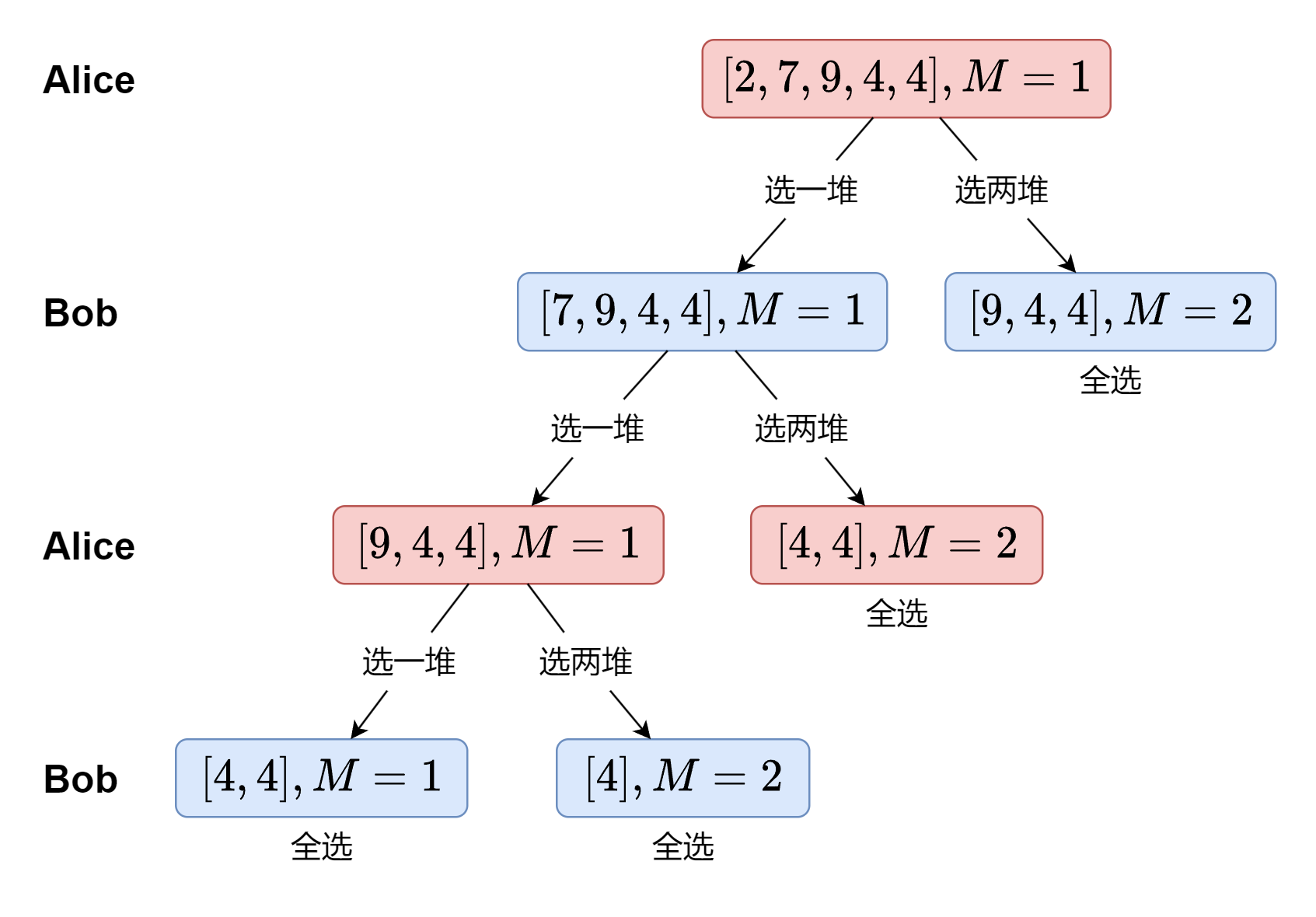
根据上图,定义dfs(i,M) 表示从]piles[i] 开始拿石子,可以得到的最大石子数。对于每个节点,由于剩余的石子总数是固定的,如果拿了某几堆石子后,对手能得到的石子数最少,那么自己能得到的石子数就是最多的。
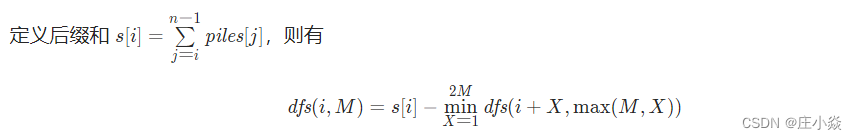
// 尚未优化,会超时
class Solution {
private int[] s;
public int stoneGameII(int[] piles) {
s = piles;
int n = s.length;
for (int i = n - 2; i >= 0; --i)
s[i] += s[i + 1]; // 后缀和
return dfs(0, 1);
}
private int dfs(int i, int m) {
if (i + m * 2 >= s.length) return s[i];
int mn = Integer.MAX_VALUE;
for (int x = 1; x <= m * 2; ++x)
mn = Math.min(mn, dfs(i + x, Math.max(m, x)));
return s[i] - mn;
}
}
由于Alice 拿一堆,Bob 拿两堆和Alice 拿两堆,Bob 拿一堆,都会递归到 dfs(3,2)。整个回溯过程是有大量重复递归调用的。由于递归函数没有副作用,无论调用dfs(i,M) 多少次,算出来的结果都是一样的,因此可以用记忆化搜索来优化:
- 如果一个状态(递归入参)是第一次遇到,那么可以在返回前,把状态及其结果记到一个 cachecache 数组(或者哈希表)中;
- 如果一个状态不是第一次遇到,那么直接返回 cache中保存的结果。
我要用二维数组记录的话,第二个维度开多大空间比较合适?或者说,需要被记忆化的M的上界是多少?两人交替拿石子,为了在 i 尽量小的情况下,使 M 尽量大,那么每次都拿满M堆,最后有(2+4+8+⋯+M)+2M<n。即4M−2<n,亦为 4M≤n+1,这样算的话 M 的上界为(n+1)/4。注意后面可以根据 n 来调整,不一定要拿满2M。总而言之,需要被记忆化的 M 的上界为(n+1)/4。
class Solution {
private int[][] cache;
private int[] s;
public int stoneGameII(int[] piles) {
s = piles;
int n = s.length;
for (int i = n - 2; i >= 0; --i)
s[i] += s[i + 1]; // 后缀和
cache = new int[n - 1][(n + 1) / 4 + 1];
for (int i = 0; i < n - 1; i++)
Arrays.fill(cache[i], -1); // -1 表示没有访问过
return dfs(0, 1);
}
private int dfs(int i, int m) {
if (i + m * 2 >= s.length) return s[i];
if (cache[i][m] != -1) return cache[i][m];
int mn = Integer.MAX_VALUE;
for (int x = 1; x <= m * 2; ++x)
mn = Math.min(mn, dfs(i + x, Math.max(m, x)));
return cache[i][m] = s[i] - mn;
}
}复杂度分析
- 时间复杂度:时间复杂度O(n^3)。记忆化后,每个状态只会计算一次,因此时间复杂度 == 状态个数×单个状态的计算时间。本题中状态个数等于O(n^2),而单个状态的计算时间为O(n),因此时间复杂度为O(n^3)。
- 空间复杂度:O(n^2)。记忆化需要存储O(n^2) 个状态。
二、动态规划解析(2)
本题很明显要用记忆化搜索或者动态规划来求解,如果直接使用动态规划的话,我们要想清楚有哪些子状态需要存储。
首先一定要存储的是取到某一个位置时,已经得到的最大值或者后面能得到的最大值,但是光有位置是不够的,相同的位置有不同数量的堆可以取,所以我们还需存储当前的M值。
由于本题中的状态是从后往前递推的,如:假如最后只剩一堆,一定能算出来最佳方案,但是剩很多堆时不好算(依赖后面的状态)。所以我们选择从后往前递推。
dp[i][j]表示剩余[i : len - 1]堆时,M = j的情况下,先取的人能获得的最多石子数
- i + 2M >= len, dp[i][M] = sum[i : len - 1], 剩下的堆数能够直接全部取走,那么最优的情况就是剩下的石子总和。
-
i + 2M < len, dp[i][M] = max(dp[i][M], sum[i : len - 1] - dp[i + x][max(M, x)]), 其中 1 <= x <= 2M,剩下的堆数不能全部取走,那么最优情况就是让下一个人取的更少。对于我所有的x取值,下一个人从x开始取起,M变为max(M, x),所以下一个人能取dp[i + x][max(M, x)],我最多能取sum[i : len - 1] - dp[i + x],[max(M, x)]。
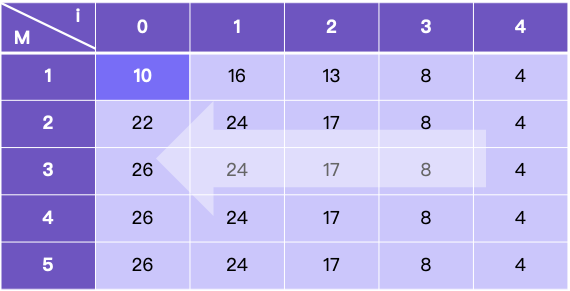
对于piles = [2,7,9,4,4],我们可以得到下图所示的dp数组,结果为dp[0][1]。
public int stoneGameII(int[] piles) {
int len = piles.length, sum = 0;
int[][] dp = new int[len][len + 1];
for (int i = len - 1; i >= 0; i--) {
sum += piles[i];
for (int M = 1; M <= len; M++) {
if (i + 2 * M >= len) {
dp[i][M] = sum;
} else {
for (int x = 1; x <= 2 * M; x++) {
dp[i][M] = Math.max(dp[i][M], sum - dp[i + x][Math.max(M, x)]);
}
}
}
}
return dp[0][1];
}博文参考
《leetcode》