文章目录

前言
一、树形结构
- 1.树的定义
- 2.树的概念（术语）
- 3.树的存储结构
二、二叉树
- 1.二叉树的概念
- - 两种特殊的二叉树
- 2.二叉树的性质
- 3.二叉树的存储结构
- 4.二叉树的基本操作
- - 4.1 二叉树的前序遍历--Preorder Traversal
  - 4.2 二叉树的中序遍历--Inorder Traversal
  - 4.3 二叉树的后序遍历--Postorder Traversal
  - 4.4 二叉树的层序遍历--levelOrde
  - 4.5 获取树中节点的个数 -- size
  - 4.6 获取叶子节点的个数 -- getLeafNodeCount
  - 4.7 获取第K层节点的个数 -- getKLevelNodeCount
  - 4.8 获取二叉树的高度 -- getHeight
  - 4.9 检测值为value的元素是否存在 -- find
总结

前言

前几篇文章介绍了数据结构中线性结构：顺序表，链表，栈，队列，并进行了模拟实现，理解了线性结构的原理和相关知识。但是我们知道，线性结构都是一对一的关系，如果处理一对多的情况，就需要使用树形结构

树形结构包括：二叉树，VAl树，B树，红黑树… 今天主要介绍 二叉树 的相关知识，在此之前要先了解什么是树形结构

二叉树是VAl树，B树，红黑树… 的基础, 学好了二叉树才能在后续学习更难的树时得心应手

提示：是正在努力进步的小菜鸟一只，如有大佬发现文章欠佳之处欢迎评论区指点~ 废话不多说，直接发车~

一、树形结构

1.树的定义

《大话数据结构》中对树这样定义：
树( Tree ) 是 n ( n >= 0 ) 个结点的有限集。n=0 时称为空树，在任意一棵非空树中：
(1) 有且仅有 1 个特定的称为 根( Tree ) 的结点
(2) n>1 时，其余结点可分为 ( m>0 ) 个互不相变的有限集T1 、T2、……、Tm，其中每一个集合本身又是一棵树，并且称为 根的子树( SubTree )

啥意思？直接看图：
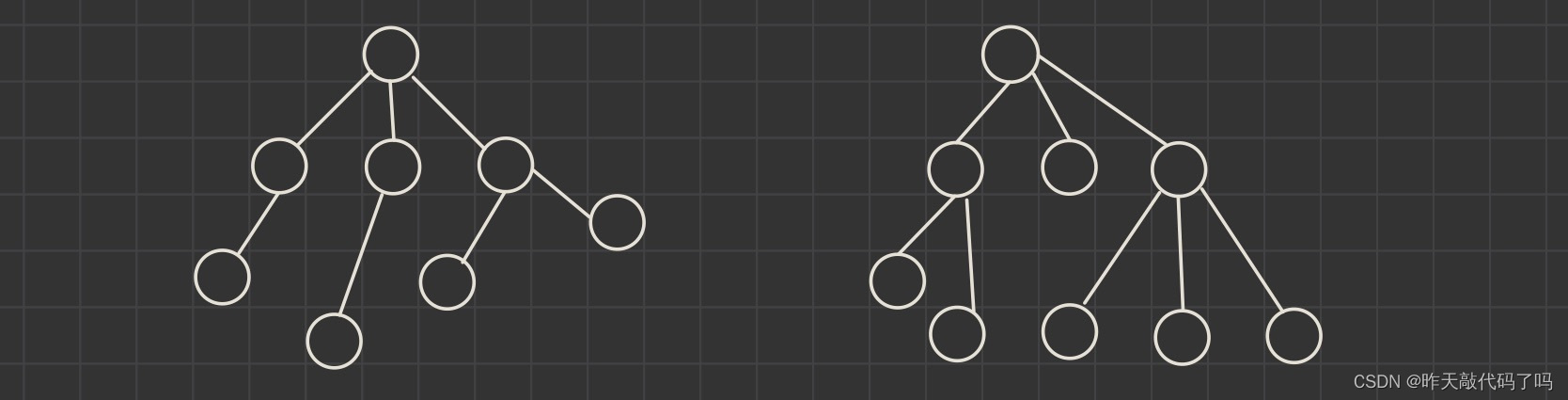
在这里插入图片描述

注意
1，有且仅有一个根结点
2，正因为子树的存在，子树T1也是树，所以树形结构是递归定义的
3，子树之间不能相交——如图所示：
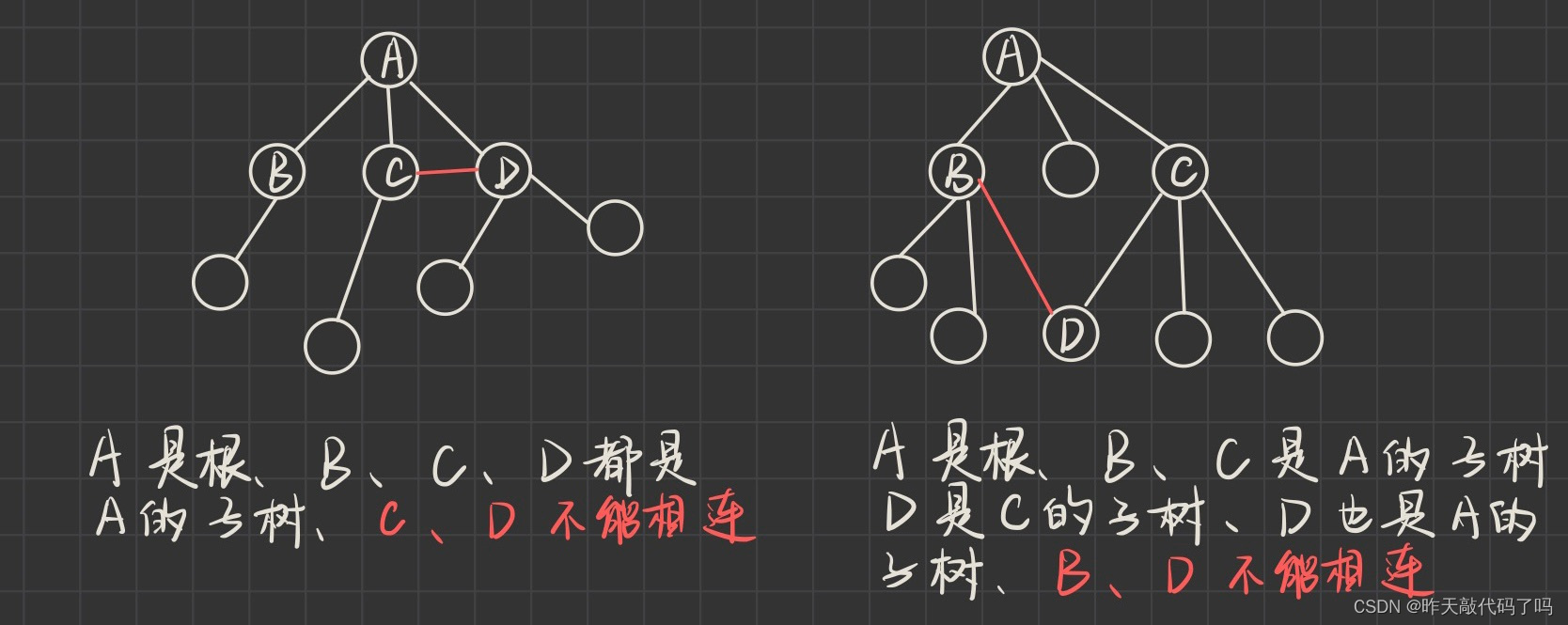
在这里插入图片描述

子树之间不能相交，所以得出结论：
1，除根结点外，一个结点只有一个父结点
2，一棵树有N个结点，则有N-1条边

2.树的概念（术语）

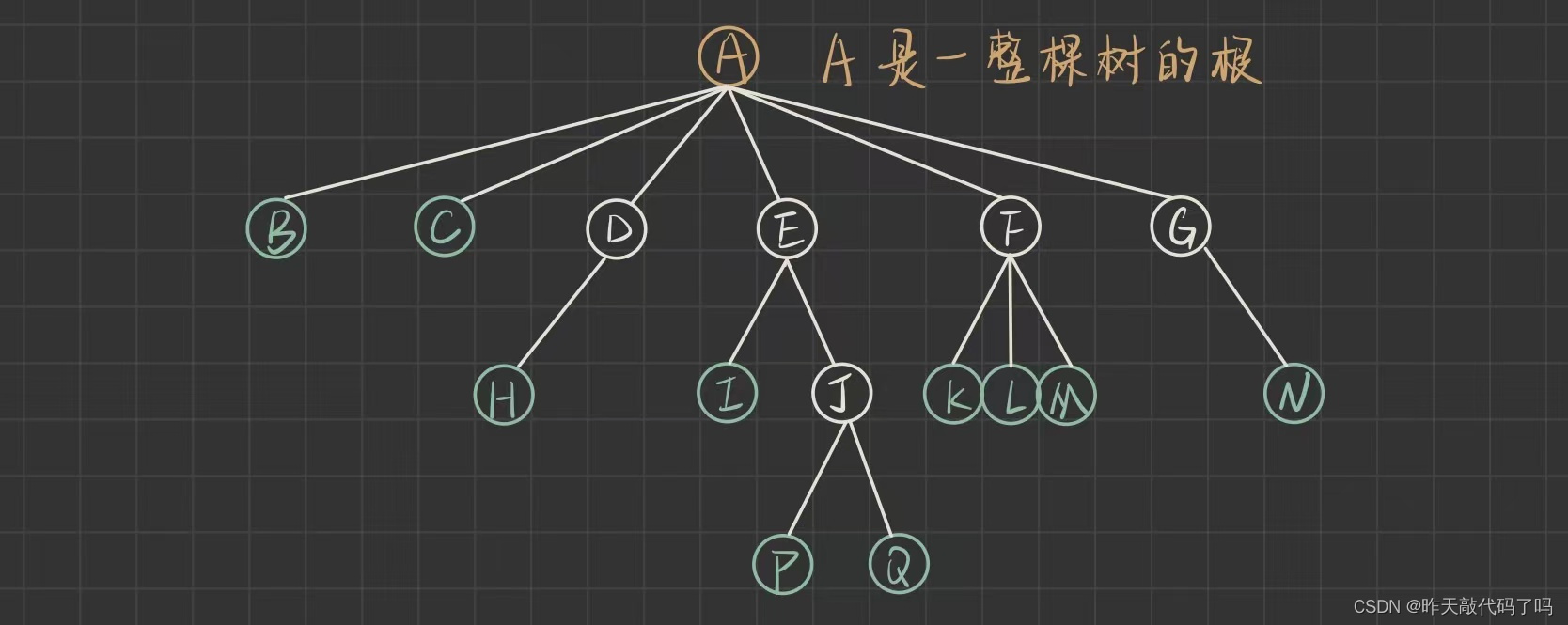
在这里插入图片描述

必会：
结点的度：一个结点含有子树的个数称为该结点的度；如上图：A的度为6

树的度：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为6

叶子结点或终端结点：度为0的结点称为叶结点；如上图：B、C、H、I…等绿色的节点为叶结点

双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是B的父结点

孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；如上图：B是A的孩子结点

根结点：一棵树中，没有双亲结点的结点；如上图：A

结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推

树的高度或深度：树的层数；如上图：树的高度为4

了解：
非终端结点或分支结点：度不为0的结点；如上图：D、E、F、G…等节点为分支结点

兄弟结点：具有相同父结点的结点互称为兄弟结点；如上图：B、C是兄弟结点

堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为堂兄弟结点

结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先, E 是 I, Q 的祖先

子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙

森林：由m（m>=0）棵互不相交的树组成的集合称为森林

3.树的存储结构

线性表中，存储结构都相对简单，但树形结构的存储结构比较复杂，并且有很多种：双亲表示法，孩子表示法、孩子双亲表示法、孩子兄弟表示法等等，这里先了解即可

二、二叉树

1.二叉树的概念

二叉树，顾名思义就是 一个结点最多有两个叉 ，两个叉分别叫 左子树 和 右子树, 既然被称作左右子树, 那么也是一棵树
二叉树的每一个结点都可以当作一棵二叉树的根节点, 所以二叉树十分满足递归的特点

如图：
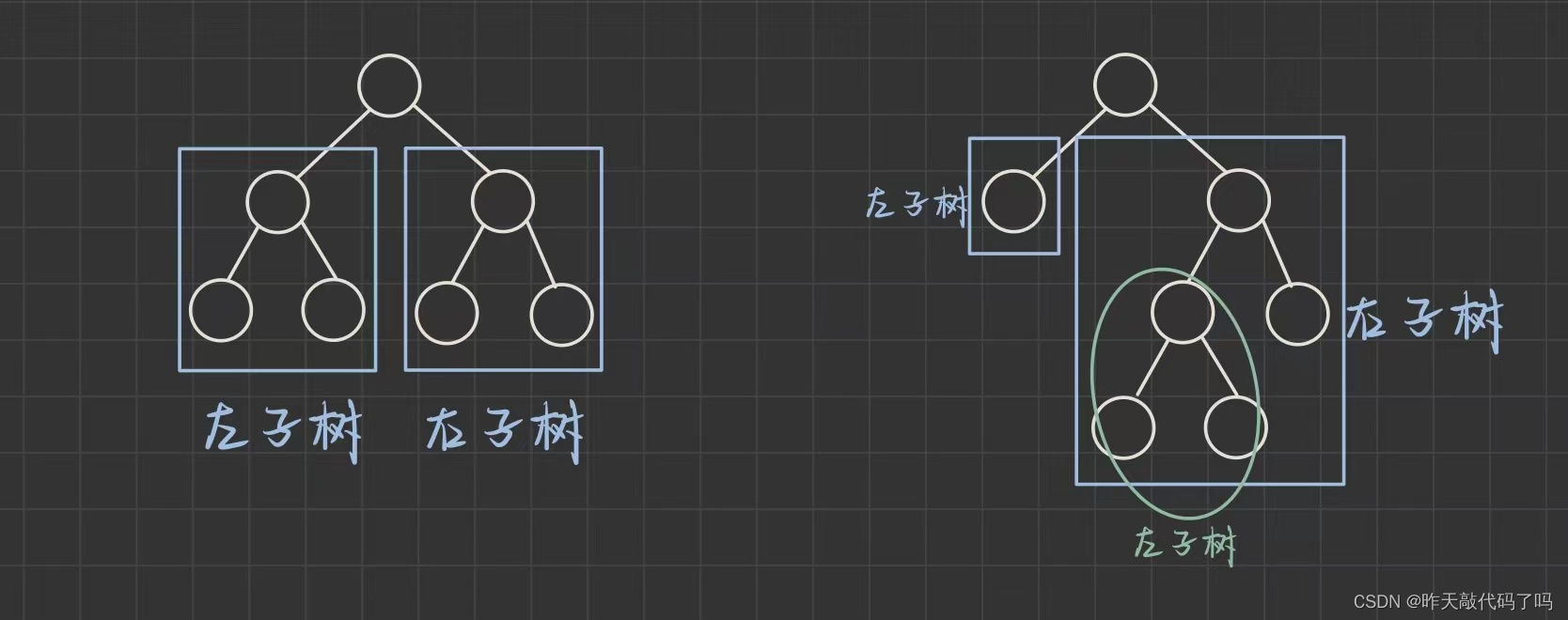
在这里插入图片描述

那么每一个结点的度最多为2，二叉树的结点可以只有一个叉，可以是“左叉”，也可以是“右叉”，如图：
在这里插入图片描述
但需要注意：如果这个结点没有 “左叉” 只有 “右叉” ，那么“右叉”也称为右子树，而不能称为左子树，因为二叉树是有序树

两种特殊的二叉树

1，满二叉树
大白话解释：每一个子树都“长满了叉”，不存在只有一个叉的结点，如图：
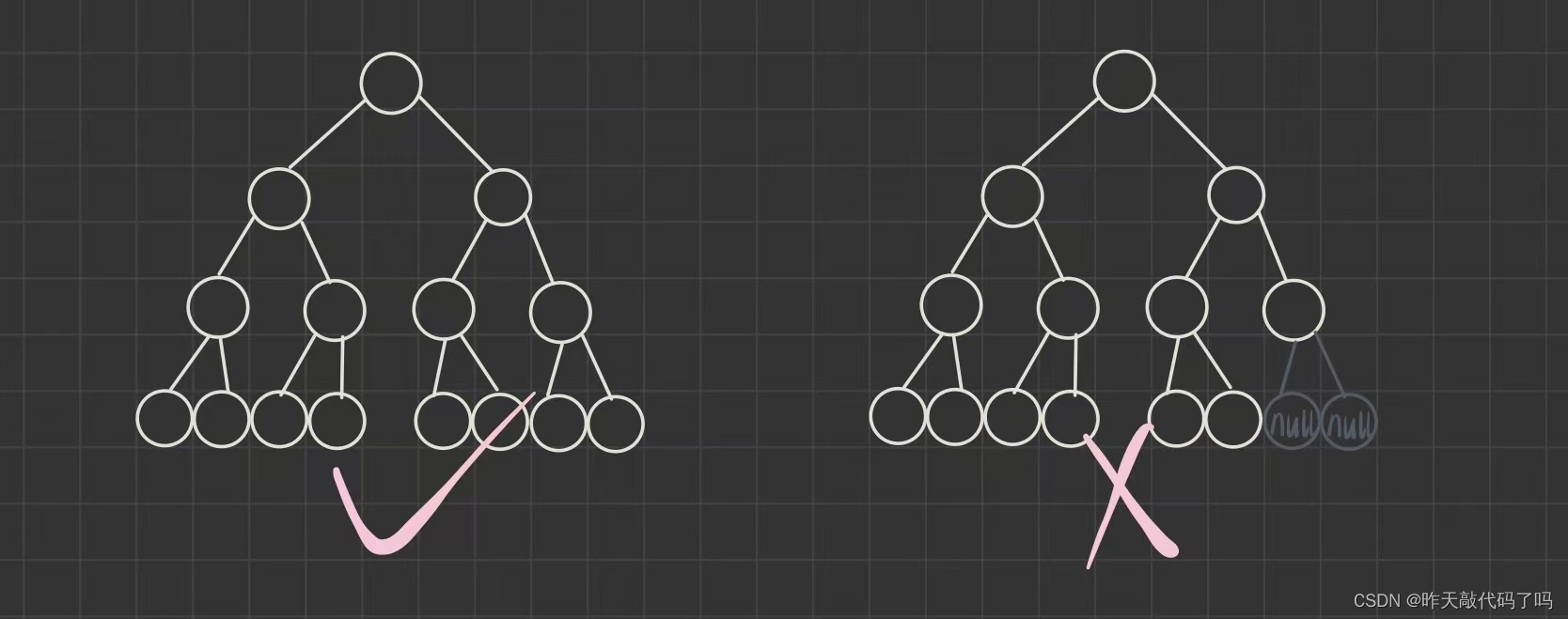
在这里插入图片描述
右边那棵树有四层, 但第四层没有长发育好, 第三层的最右边叶子结点没有左右子树, 它不是满二叉树

2，完全二叉树
大白话解释：结点可以只有一个叉，但不能只有 “右叉” 而没有 “左叉” ，或者有左叉而没有右叉时, 右边还有结点, 如图：
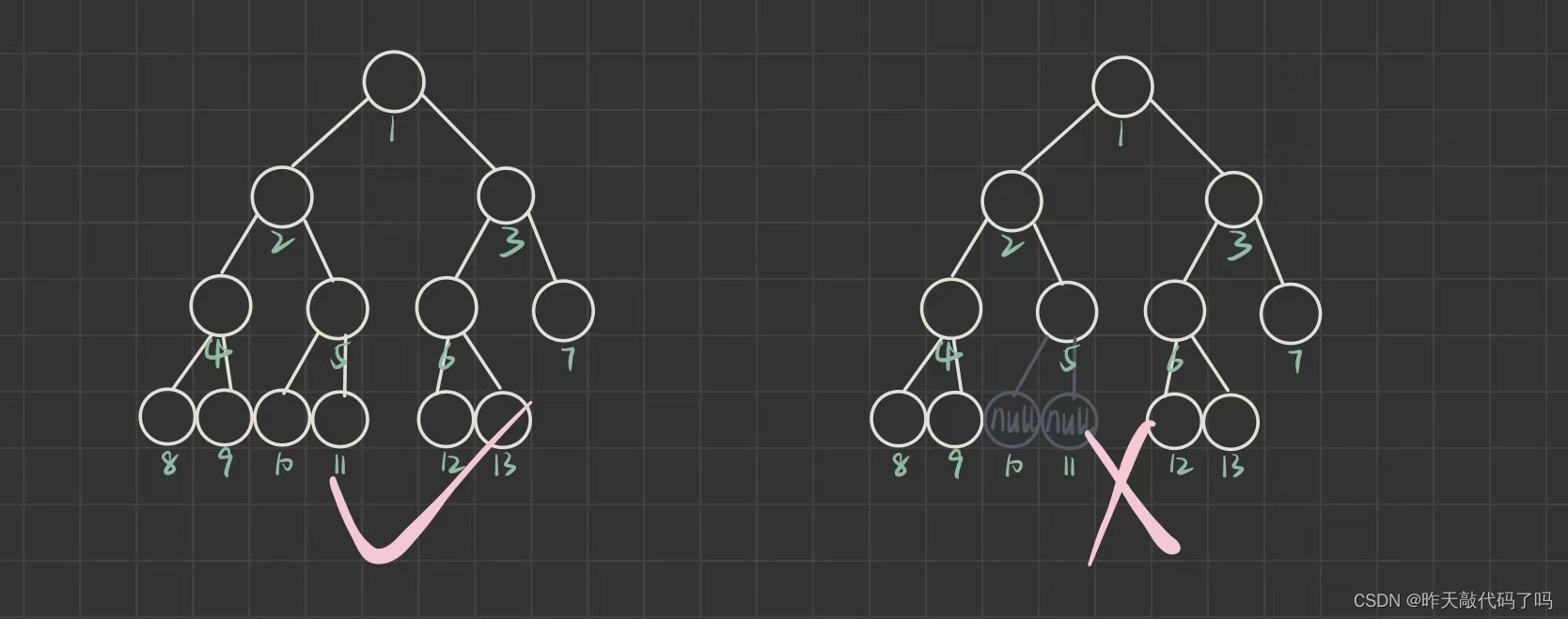
在这里插入图片描述
每一棵树按从左往后从上到下的顺序标号, 每一个结点对应一个下标时就是完全二叉树
右边那棵树的10,11下标处没有结点, 但12,13下标有结点, 它就不是完全二叉树

堆这种结构就是顺序存储的完全二叉树

2.二叉树的性质

若规定根结点的层数为1，则一棵非空二叉树的第 i 层上最多有2^(i-1) 个结点(i>0)

若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 2^k - 1个(k>=0)

对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1

具有n个结点的完全二叉树的深度k为 log₂(n+1)上取整

对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为 i 的结点有：
1.若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
2.若2i+1<n，左孩子序号：2i+1，否则无左孩子
3.若2i+2<n，右孩子序号：2i+2，否则无右孩子
这一点了解即可, 后续分享 [优先级队列 — 堆] 相关内容时会再介绍

3.二叉树的存储结构

二叉树的存储结构分为顺序存储和链式存储, 一般主要以链式存储为主, 以顺序结构存储的二叉树称作 "堆 "

二叉树的链式存储结构就像链表那样, 是由一个个结点链接而成, 每个结点中有三个域: 一个值域和两个指针域 , 两个指针域分别是这个结点的左右子树的地址
回顾链表的模拟实现方式, 每个结点都是 binaryTree 这个类的内部类, 所以上述的三个域就是三个内部类的成员属性

binaryTree 还需要一个成员属性 root 来记录二叉树的根节点

链式存储主要以孩子表示法为主

public class binaryTree {
    private static class treeNode {
        private char val;
        private treeNode left;
        private treeNode right;

        public treeNode(char val) {
            this.val = val;
        }
    }
    private treeNode boot;
}

4.二叉树的基本操作

4.1 二叉树的前序遍历–Preorder Traversal

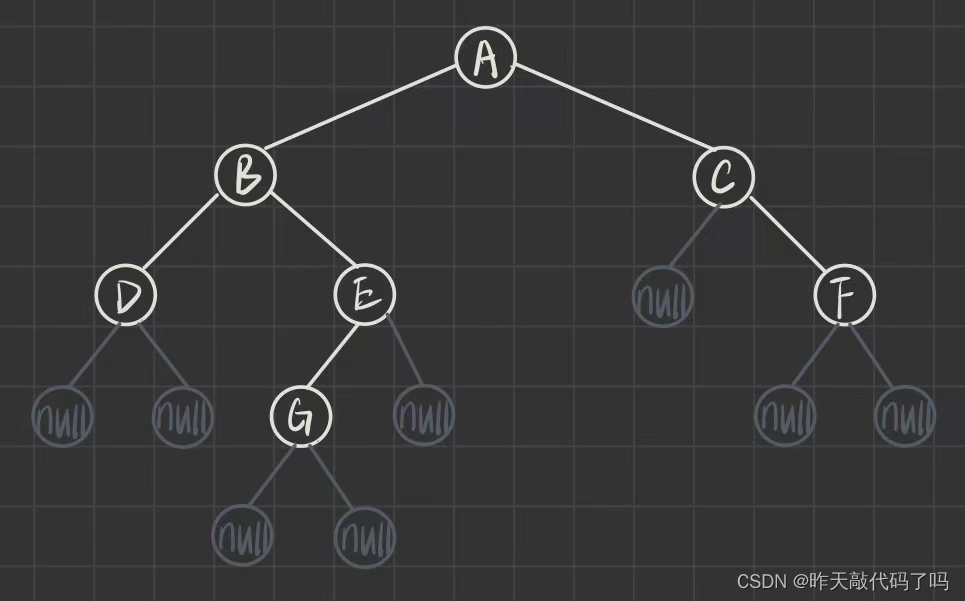
在这里插入图片描述

前序遍历是指, 从根节点开始, 先访问根节点, 再访问左子树, 再访问右子树, 对于每一颗树来说都是这样的访问顺序. 简称 "根左右" 的顺序

这个顺序对每一颗树来说都相同: 那么当二叉树的根节点访问完之后应该访问这个根结点的左子树, 那么这棵左子树也是树, 同样需要按照 “根左右” 的顺序访问…这就是递归, 来看图解:
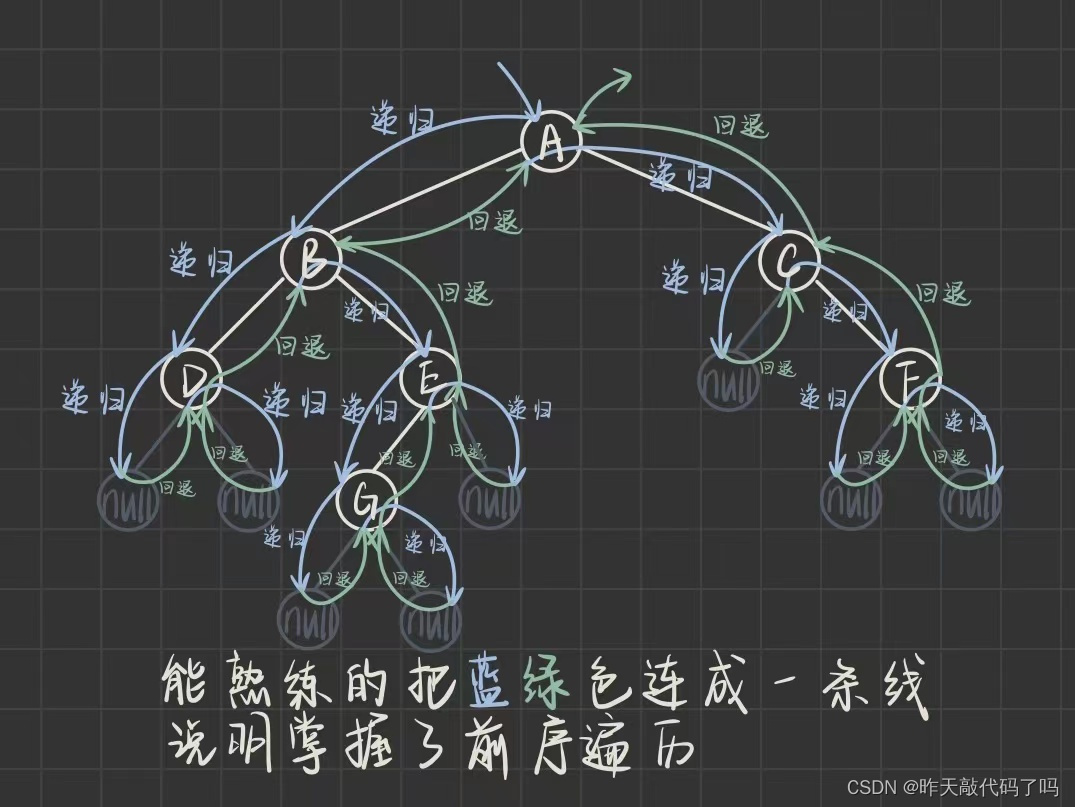
在这里插入图片描述
前序遍历序列: ABDEGCF

每次递归都要递归到叶子结点为止, 而这个叶子结点是没有左右子树的, 所以递归的终止条件就是 root == null
来看代码如何实现:;

   public void preorderTraversal(treeNode root) {
        if (root == null) {
            return;
        }
        System.out.println(root.val);
        prevOrder(root.left);
        prevOrder(root.right);
    }

代码非常简单, 只需要写出递归的终止条件, 然后先打印, 再把这个结点的左子树传参,再把这个结点的右子树传参

上述写法的思路是遍历每一个结点并访问, 属于遍历思想, 而二叉树的学习中还有子问题思想是经常需要用到的

如果把 preorderTraversal() 这个方法的返回值改成 List< Integer > 应该怎么写呢?
应该很简单, 只需要给一个 List 对象, 把刚刚的打印操作改成 add 操作即可:

   public List<Integer> list = new ArrayList<>();
   public List<Integer> preorderTraversal(treeNode root) {
        if (root == null) {
            return list;
        }
        list.add(root.val);
        prevOrder(root.left);
        prevOrder(root.right);
        return list
    }

这样的写法仍然是遍历思想, 只是一个一个结点的, 把访问的方式从打印变成 add

请注意, 在上述代码中, 左右递归时,好像并没有接收返回值呀, 明明有返回值, 但应该如何接收呢 ? 或者说, 接收返回值能有什么用呢?
对于二叉树的每一个结点来说, 都可以当作一棵树的根结点, 我们需要返回一整棵树的前序遍历得到的 List , 那么就可以想, 如果在 list 中 add 上根节点自己的 val 值, 再 add 上根节点的左右子树的 List 中的每一个值, 不就得到整颗树的 List 了吗


   public List<Integer> preorderTraversal(treeNode root) {
     	public List<Integer> list = new ArrayList<>();
        if (root == null) {
            return list;
        }
        list.add(root.val);
        List<Integer> leftList = prevOrder(root.left);
        list.addAll(leftList);// 把左树的List集合全部add到list中
        List<Integer> rightList = prevOrder(root.right);
        list.addAll(rightList);// 把右树的List集合全部add到list中
        return list
    }

这样一来, 返回值也用到了, 并且是标准的子问题思想

对于返回值是 List 集合这种前序遍历来说:
遍历思想的解决方式是 — 遇到一个结点就 add
子问题思想的解决方式是 — add 根节点 + add 左子树所有节点 + add 右子树所有节点

这里只是先提一下子问题思想的方式, 后面还有很多地方要用到子问题思想, 熟练掌握运用这种思想也不是一蹴而就的, 需要日积月累的锻炼

4.2 二叉树的中序遍历–Inorder Traversal

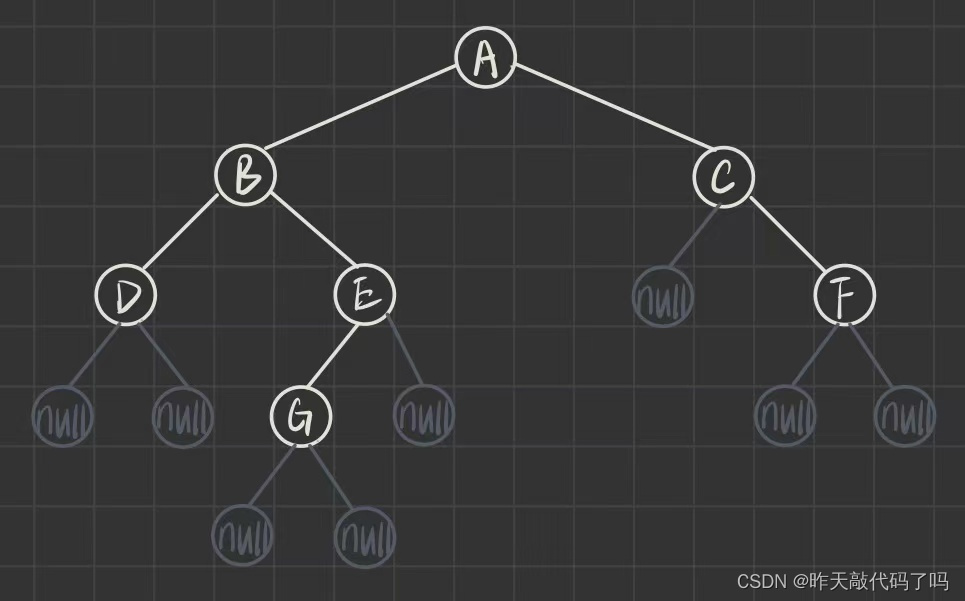
在这里插入图片描述

中序遍历是指, 从根节点开始, 先访问左子树, 再访问根节点, 再访问右子树, 对于每一颗树来说都是这样的访问顺序. 简称 "左根右" 的顺序

这个顺序对每一颗树来说都相同: 先访问二叉树的根节点的左子树, 那么这棵左子树也是树, 同样需要按照 “根左右” 的顺序访问…当左子树全部访问完后, 返回到父节点并访问,然后再访问父节点的右子树…

利用子问题思想也是可以写出来的噢

中序遍历序列:DBGEACF

递归思想和前序遍历是一致的, 那么代码中只需要更改一下打印结点的位置即可:

   public void inorderTraversal(treeNode root) {
        if (root == null) {
            return;
        }
        prevOrder(root.left);
        System.out.println(root.val);
        prevOrder(root.right);
    }

利用子问题思想也是可以写出来的噢

4.3 二叉树的后序遍历–Postorder Traversal

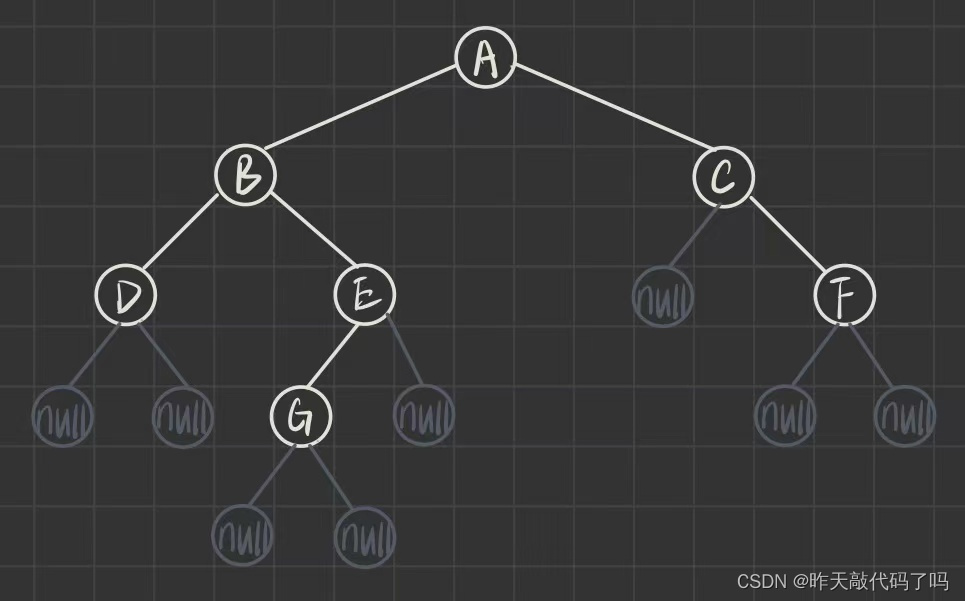
在这里插入图片描述

后序遍历是指, 从根节点开始, 先访问左子树, 再访问右子树, 再访问根节点, 对于每一颗树来说都是这样的访问顺序. 简称 "左右根" 的顺序

这个顺序对每一颗树来说都相同: 先访问二叉树的根节点的左子树, 那么这棵左子树也是树, 同样需要按照 “根左右” 的顺序访问…当左子树全部访问完后, 再访问父节点的右子树…同样需要按照 “根左右” 的顺序访问…当左右子树都访问完后, 再返回到父节点并访问

后序遍历序列: DGEBFCA

递归思想和前序遍历中序遍历是一致的, 那么代码中只需要更改一下打印结点的位置即可:

   public void postorderTraversal(treeNode root) {
        if (root == null) {
            return;
        }
        prevOrder(root.left);
        prevOrder(root.right);
        System.out.println(root.val);
    }

4.4 二叉树的层序遍历–levelOrde

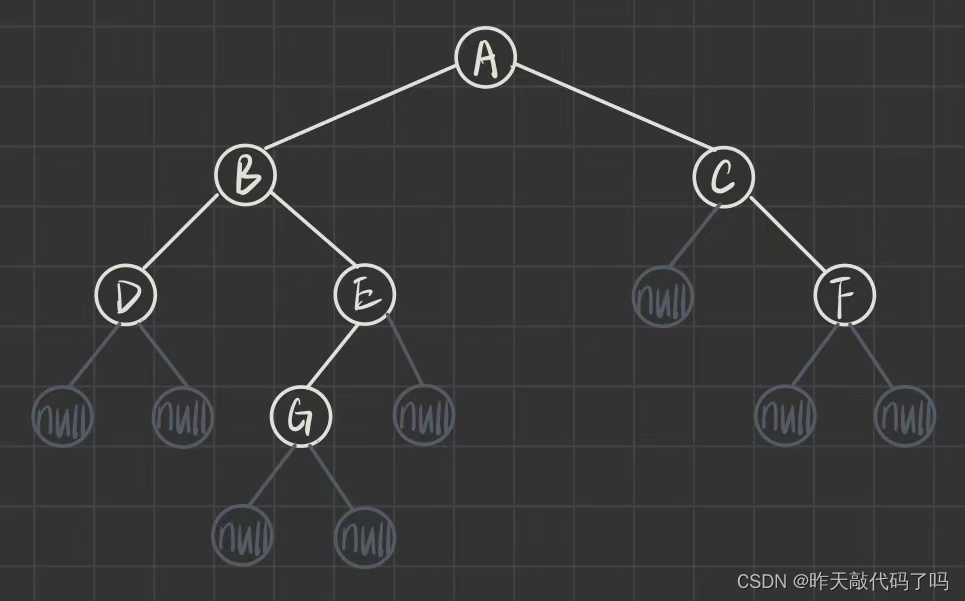
在这里插入图片描述
层序遍历非常简单, 就是看二叉树有几层, 每层从左往右的顺序访问即可

层序遍历序列: ABCDEFG

层序遍历没有递归的思想,而是利用循环就可以做到, 需要借助一个队列, 先让根结点入队, 然后当队列不为空时循环, 让队列中的结点依次出队,令它为top , 如果 top 有左右孩子结点就让左右孩子结点入队, 循环结束代表每个结点都访问过了

    public void levelOrder(treeNode root){
        if(root == null) {
            return;
        }
        Queue<treeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            treeNode node = queue.poll();
            System.out.println(node.value + " ");
            if(node.left != null) {
                queue.offer(node.left);
            }
            if(node.right != null) {
                queue.offer(node.right);
            }
        }

4.5 获取树中节点的个数 – size

已经学习过了各种遍历, 求节点个数就很简单了, 只需要定义一个变量 count , 在遍历到每一个结点时, 让count++即可
这是遍历思想的实现, 不再赘述代码, 主要介绍子问题思想的实现:

问题是求所有结点的个数, 那么把这个问题的所有子问题就是 : 求根节点的个数 + 左子树所有结点的个数 + 右子树所有结点的个数
根节点个数肯定就是1, 那么二叉树的叶子节点算不算一棵树的根节点呢?
肯定算, 不过这棵树只有根节点, 没有左右子树而已

    public int size(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftSize = size(root.left);
        int rightSize = size(root.right);
        return leftSize + rightSize + 1;
    }

4.6 获取叶子节点的个数 – getLeafNodeCount

同样, 用子问题思想的解决方法是: 左树的叶子节点个数 + 右树叶子节点的个数

    int getLeafNodeCount(TreeNode root) {
        if(root == null) {
            return 0;
        }
        if(root.left == null && root.right == null){
            return 1;
        }
        int leftSize = getLeafNodeCount(root.left);
        int rightSize = getLeafNodeCount(root.right);
        return leftSize+rightSize;
    }

4.7 获取第K层节点的个数 – getKLevelNodeCount

同样, 用子问题思想的解决方法是: 左树的第 K 层结点个数 + 右树第 K 层的个数
如何求第 K 层结点个数呢? 反正 root 都会递归遍历到每一层的每一个结点, 只需要定义一个遍历 K, root 每走一层就让 K - 1, 当 K 等于 1 时,root 所在的这一层就是第 K 层, 返回个数(1)即可

    int getKLevelNodeCount(TreeNode root,int k) {
        if(root == null) {
            return 0;
        }
        if(k == 1) {
            return 1;
        }
        int leftSize = getKLevelNodeCount(root.left,k-1);
        int rightSize = getKLevelNodeCount(root.right,k-1);
        return leftSize + rightSize;
    }

4.8 获取二叉树的高度 – getHeight

首先明确一个问题: 高度为1的树是什么样子? 只有一个结点, 没有左右子树

之前的子问题思路都是左子树的…加上右子树的…, 现在的问题是求二叉树的高度, 那么这就要涉及到左右子树的高度的比较了
对于满二叉树来说, 根节点的左右子树高度肯定是一样的, 那其他情况呢? 左右子树高度不平衡, 这就需要先求出左子树高度, 再求出右子树高度, 如果左子树比右子树高就让左子树+1, 如果右子树比左子树高就让右子树+1

哎? 不对啊,为啥还要给高的那棵树再+1呢?
再看一遍原话, 是先求左右子树的高度, 是子树!!

比如开学第一天,你的老师让你统计一下全班的人数, 你把所有人都查了一遍, 结果忘了算你自己

我们把左右子树的较高的那棵树找到之后, 再+1 就是整棵树的高度, 所以
+1, 加的是根节点本身的高度

    public int getHeight(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);

        return (leftHeight > rightHeight) ?
                (leftHeight+1):(rightHeight+1);
    }

4.9 检测值为value的元素是否存在 – find

先往左子树找, 如果找到了就不去右子树, 直接返回, 如果没找到就去右子树找, 找到了就返回, 如果还没找到就是真没找到

    TreeNode find(TreeNode root, int val) {
        if(root == null) {
            return null;
        }
        if(root.val == val) {
            return root;
        }
        TreeNode leftTree = find(root.left,val);
        if(leftTree != null) {
            return leftTree;
        }
        TreeNode rightTree = find(root.right,val);
        if(rightTree != null) {
            return rightTree;
        }
        return null;//没有找到
    }