👦个人主页:Weraphael
✍🏻作者简介:目前正在学习c++和算法
✈️专栏:【C/C++】算法
🐋 希望大家多多支持,咱一起进步!😁
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍
回顾
- 一维前缀和 + 二维前缀和
目录
- 回顾
- 一、一维差分
- 1.1 什么是差分
- 1.2 如何构造`b`数组
- 1.3 用途
- 1.4 代码
- 模板1
- 模板2 + 解释
- 二、二维差分
- 2.1 什么是二维差分
- 2.2 如何构建`b[i][j]`以及用途
- 2.3 代码模板
- 三、总结
一、一维差分
1.1 什么是差分
- 首先有一个原数组
a:a[1],a[2],a[3] ... a[N] - 然后构造一个数组
b:b[1],b[2],b[3]...b[N],使得a[N] = b[1] + b[2]+ b[3] + ... + b[N] - 所以,我们就称a数组是b数组的前缀和,而
b数组就称为a数组的差分
1.2 如何构造b数组
可以利用高中的知识:
一开始初始化a[0] = 0
b[1] = a[1] - a[0]
b[2] = a[2] - a[1]
b[3] = a[3] - a[2]
…
b[n] = a[n] - a[n-1]
最后再把上述式子加起来,就可以得到:a[n] = b[1] + b[2]+ b[3] + ... + b[n],所以,构造b[n]数列的公式为:b[n] = a[n] - a[n-1]
1.3 用途
假设现在有一问题:将
a数组[l,r]区间中的每一个数都加一常数C,即a[l] + c,a[l+1] + c + ... + a[r] + c(减上一个常数c也是同一个意思)
- 暴力
for循环遍历
[l,r],时间复杂度是O(n)
- 差分
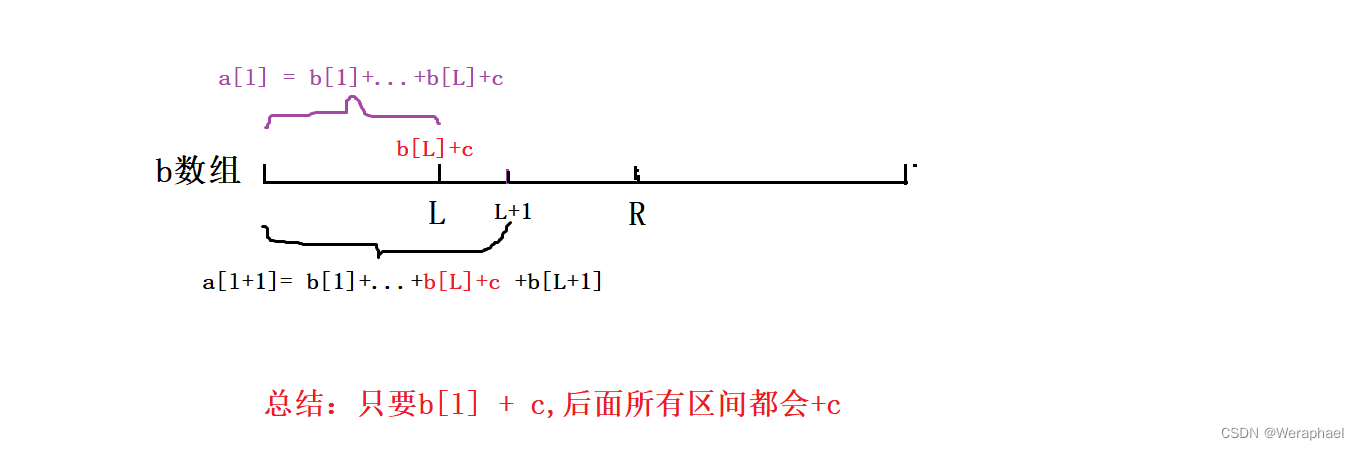
因为
a数组是b数组的前缀和:a[n] = b[1] + b[2] + b[3] + ... + b[n],只要b[l] + c,a数组在区间[l,n]都会加上c,即a[l] + c,a[l + 1] + c,...,a[n] + c,什么意思呢?画个图就豁然开朗了(如下图)
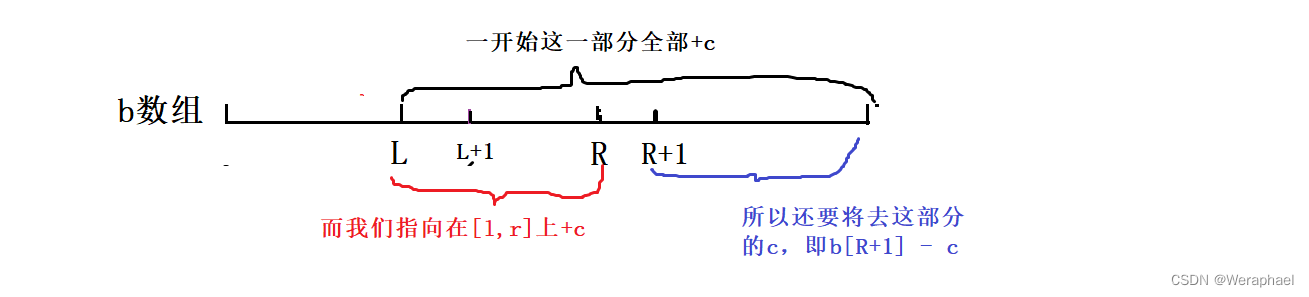
但是,a数组在区间
[l,n]都会加上c,而我们只想在[l,r]上加上c,所以数组b区间[r+1,n]每个数都要-c
一维差分总结:
- 给区间
[l,r]中的每个数加上c,b[l] += c,b[r+1] -= c,并且时间复杂度是O(1)- 下标为什么从1开始其实和前缀和是一个意思 -> 传送门
1.4 代码
模板1
#include <iostream>
using namespace std;
const int N = 10010;
int a[N],b[N];///全局变量,初始化为0
int main()
{
int n;// n - 数组元素个数
scanf("%d",&n);
//输入原数组a
for (int i = 1;i <= n;i++)
scanf("%d", &a[i]);
//构建b数组
for (int i = 1;i <= n;i++)
b[i] = a[i] - a[i - 1];
//a数组在[l,r]上,加上一个数
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
b[l] += c;
b[r + 1] -= c;
//求出+c后的数组
for (int i = 1;i <= n;i++)
b[i] = b[i - 1] + b[i];//a[i] = b[i] + a[i - 1]
//输出
for(int i = 1;i <= n;i++)
printf("%d ",b[i]);
return 0;
}
模板2 + 解释
#include <iostream>
using namespace std;
const int N = 10010;
int a[N],b[N];//全局变量,初始化为0
void insert(int l,int r,int c)
{
b[l] += c;
b[r + 1] -= c;
}
int main()
{
int n;
scanf("%d",&n);
//输入原数组a
for (int i = 1;i <= n;i++)
scanf("%d", &a[i]);
//构建b数组
for (int i = 1;i <= n;i++)
insert(i,i,a[i]);
//a数组在[l,r]上,加上一个数
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
//求出+c后的数组(前缀和)
for (int i = 1;i <= n;i++)
b[i] = b[i] + b[i - 1];//a[i] = b[i] + a[i - 1]
//输出
for(int i = 1;i <= n;i++)
printf("%d ",b[i]);
return 0;
}
解释:
首先封装了insert函数来帮助我们在某段区间加上c,而为什么构造b数组时也能使用这个函数呢?这个问题其实我也想了很久,但是其实画个图就明白了
二、二维差分
2.1 什么是二维差分
- 首先有一个原数组
a[i][j] - 然后构建一个差分数组
b[i][j],即a[n][m] = b[1][1] + b[2][1] + b[2][2] + ... + b[n][m] - 所以,我们称
a[i][j]是b[i][j]的前缀和数组,而b数组就是a数组的差分
2.2 如何构建b[i][j]以及用途
首先先讲讲用途,假设现在有一问题:已知原数组a中被选中的子矩阵是以(x1,y1)为左上角,以(x2,y2)为右下角所围成的区域,现要求在子矩阵中每个数+c
- 暴力做法
for循环遍历,时间复杂度是O(n2)
- 差分
一定要记住,
a数组是b数组的前缀和,若对b数组的b[i][j]的修改,势必会影响到a数组中从a[i][j]及往后的每一个数,时间复杂度可以由O(n2)优化成O(1)
做法如下
目的:让黄色区域所有数都加上c
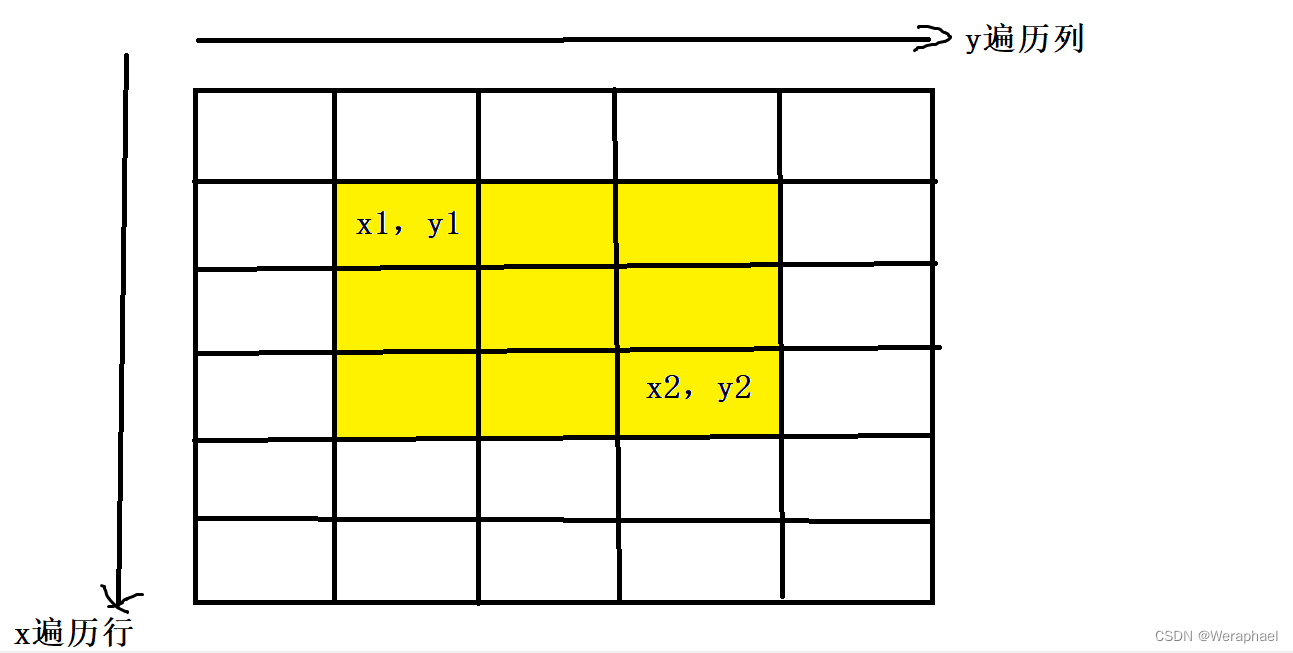
记住,a数组是b数组的前缀和,若对b数组加上c,势必会影响c。所以b[x1][y1]+c,会导致红色区域加上c
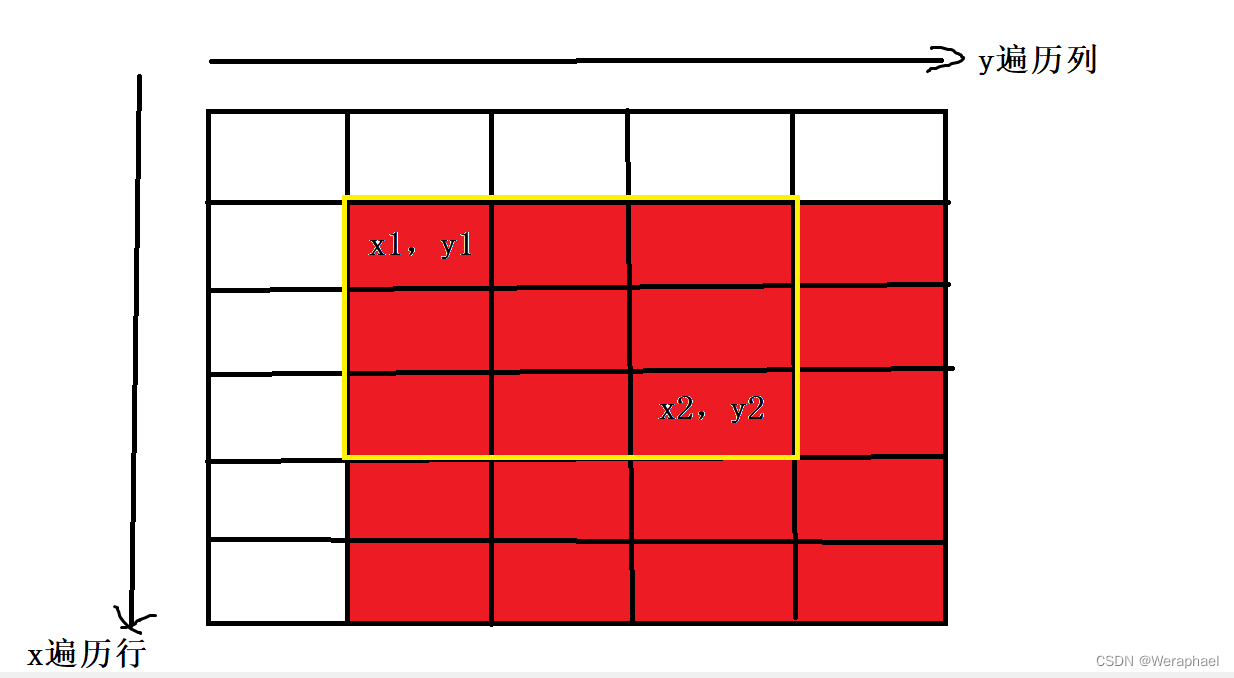
所以,现只要把绿色部分多加的c去掉即可
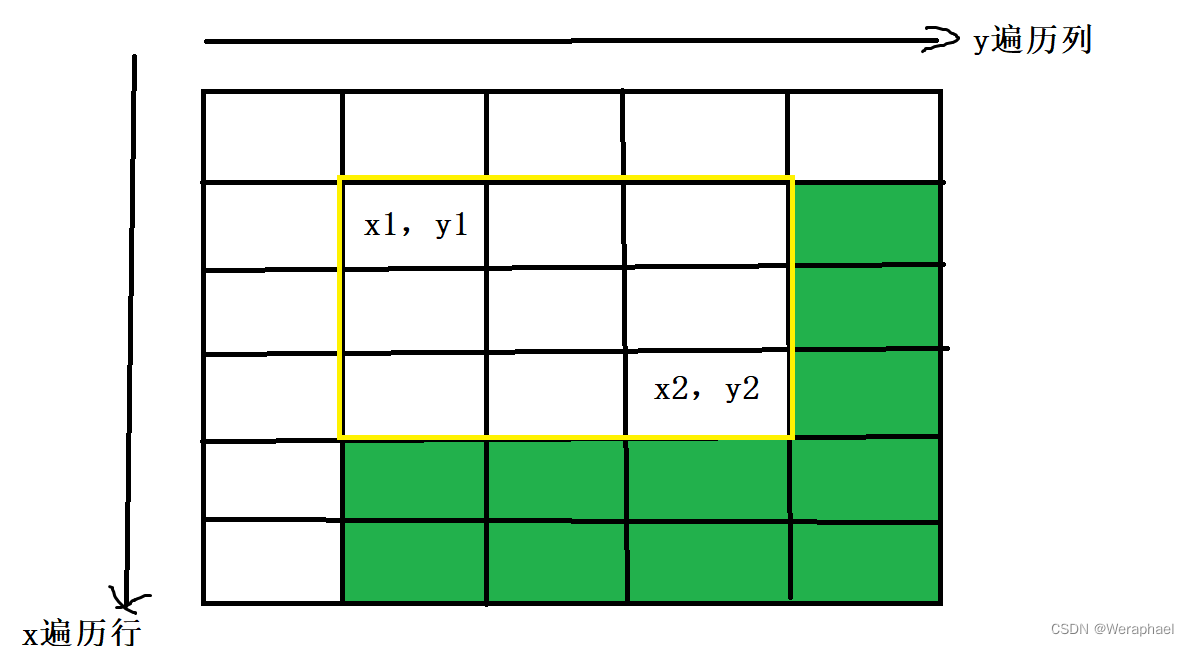
首先,先减去紫色部分多加的c
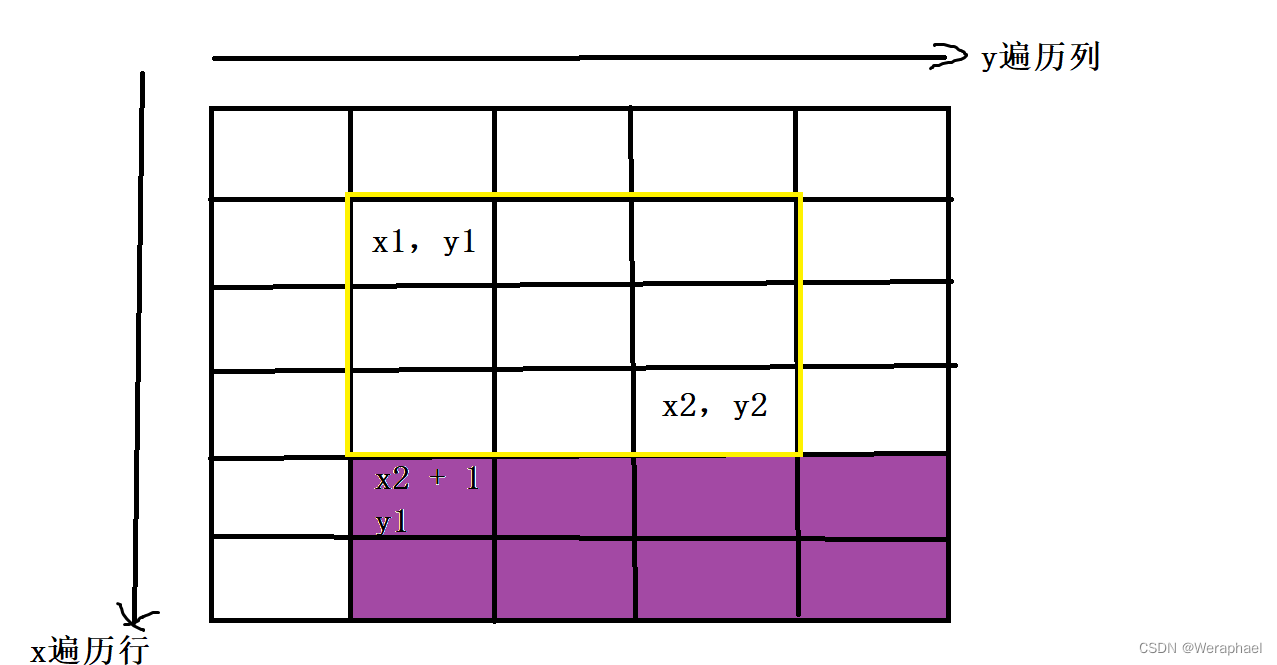
b[x2 + 1][y1] -= c
接下来再减去灰色部分多加的c
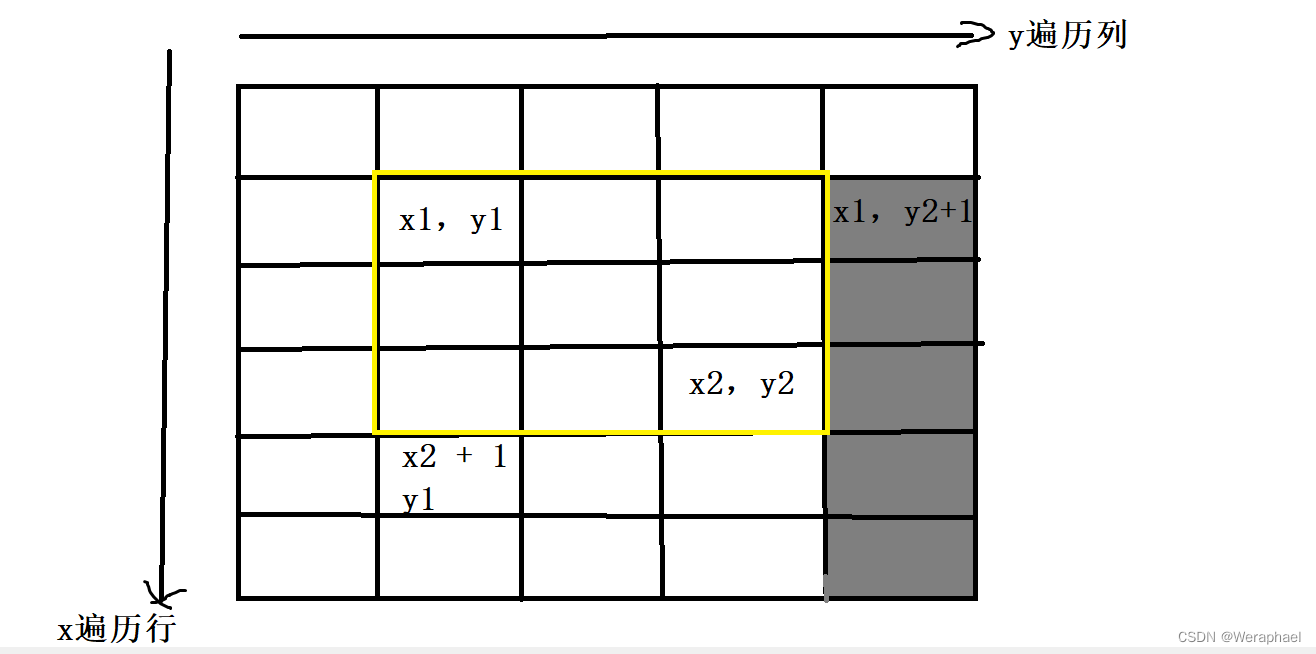
b[x1][y2 + 1] -= c
最后,由于前两步多减了橙色部分的c,所以还要再加回去
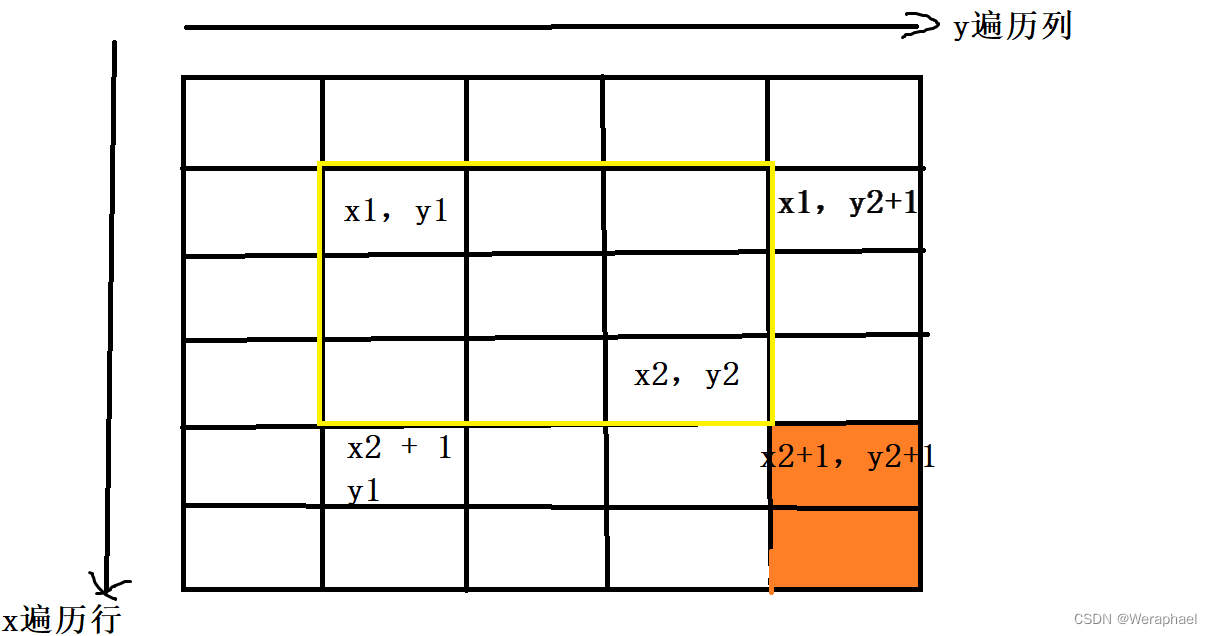
b[x2 +1 ][y2 + 1] += c
我们把上述过程封装成一个insert函数
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2+1][y1] -= c;
b[x1][y2+1] -= c;
b[x2+1][y2+1] += c;
}
最后b数组的构造也能使用这个插入函数,过程和一维差分差不多,详情请看一维差分的模板2
2.3 代码模板
#include <iostream>
using namespace std;
const int N = 10010;
int a[N][N],b[N][N];
//插入函数
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
int n,m;
scanf("%d%d%d",&n,&m);
//输入原数组a + 构造差分数组b
for (int i = 1;i <= n;i++)
{
for (int j = 1;j <= m;j++)
{
scanf("%d",&a[i][j]);
insert(i,j,i,j,a[i][j]);
}
}
//在指定子矩阵+c
int x1,y1,x2,y2,c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1,y1,x2,y2,c);
//二维前缀和
for (int i = 1;i <= n;i++)
{
for (int j = 1;j <= m;j++)
{
b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];
}
}
for (int i = 1;i <= n;i++)
{
for (int j = 1;j <= m;j++)
printf("%d ",b[i][j]);
printf("\n");
}
return 0;
}
三、总结
一维差分
void insert(int l,int r,int c)
{
b[l] += c;
b[r + 1] -= c;
}
二维差分
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}