数据结构_ 堆结构与堆排序(c++ 实现 + 完整代码 )

news2024/11/30 14:34:28

堆结构与堆排序

文章目录

  • 堆结构与堆排序
    • 引入堆
    • 堆结构所满足的数学特性
    • 准备代码
    • ----------- 往堆中插入元素
    • ----------- 删除堆顶
    • 堆排序构建
    • 完整代码及测试
      • 动态分配版本
      • 非动态版本

引入堆

  • 二叉树
    具有左孩子与右孩子的最普通的二叉树。

  • 满二叉树
    特殊的二叉树：每个节点如果有孩子则一定同时具有左孩子与右孩子。

满二叉树的条件：

  1. 要么有两个孩子，要么没有孩子
  2. 叶子节点在同一层

满二叉树有如下规律：
​如果层数为n
第n层节点数 一定为 2^(n-1)
整颗树节点数 为 2^n - 1

  • 完全二叉树
    能够使得满二叉树 从 下边和右边开始删节点的 二叉树 , 满足从右往左 从下往上删除 （和 阅读顺序 相反）

    1. 满二叉树一定是完全二叉树

    2. 完全二叉树不一定是满二叉树

  • 堆

    ​ 堆是有序的完全二叉树。

    ​ 父子之间必须有序，父大于子或者子大于父，同层兄弟之间不用管

    1. 父大于子：最大堆（大顶堆）
    2. 子大于父：最小堆（小顶堆）

堆结构所满足的数学特性

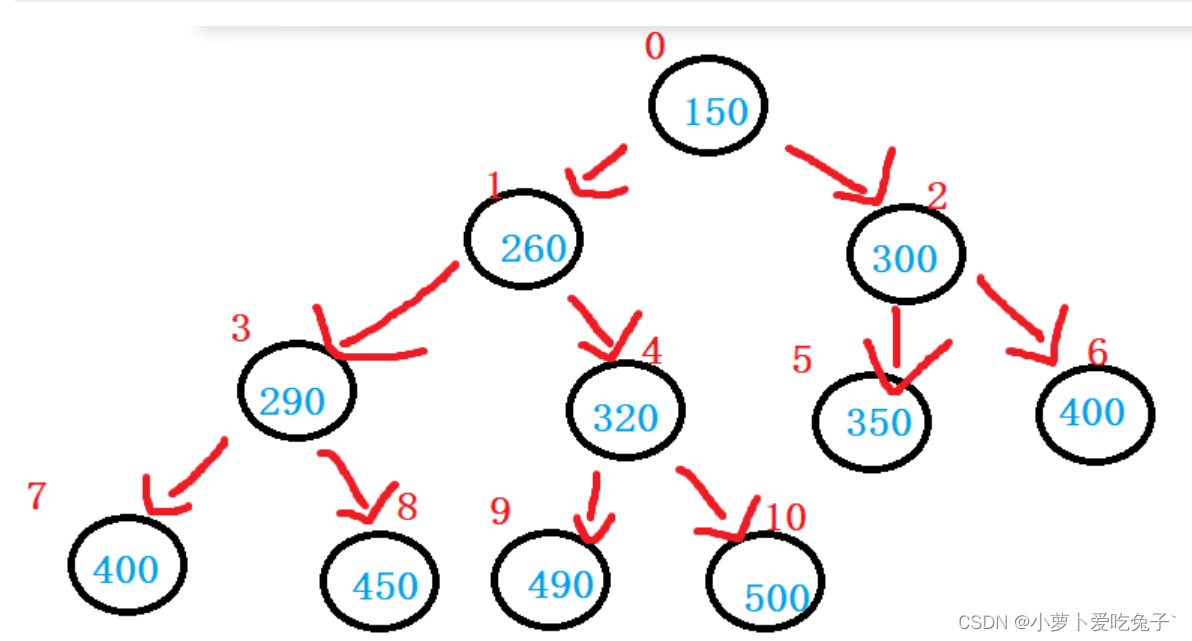
在这里插入图片描述

下标关系：

  • 150 的 下标为 0 ，260 的下标为1，290的下标为3，400的下标为7。共同点：都是父节点的左孩子，父节点的下标*2+1=左孩子的下标

  • 150的下标为0，300的下标为2，400的下标为6；260的下标为1，320的下标为4，500的下标为10。共同点：都是父节点的右孩子，父节点的下标*2+2=右孩子的下标

  • 相反，已知400的下标为7，则290的下标为3，260的下标为1。共同点：已知左孩子的下标，（左孩子下标-1）/2得到父节点的下标

  • 已知500的下标为10，320的下标为4，260 的下标为1。共同点：已知右孩子的下标，（右孩子下标-2）/2得到父节点的下标

    总结：

    父亲推孩子：

    已知父节点下标为N
    左孩子下标为：2*N + 1

    右孩子下标为：2*N + 2

    孩子反推父亲：

    已知左孩子下标为M 父节点下标为： (M-1)/2
    已知右孩子下标为M 父节点下标为： (M-2)/2

    已知孩子下标为M 父节点下标为： (M-1)/2

准备代码

template <class T>
class My_Heap
{
private:
	T* pRoot;	//指向堆的指针，实际上是一个动态数组
	int len;	//元素个数
	int MaxLen;	//容量
public:
	My_Heap()
	{
		pRoot = nullptr;
		len = MaxLen = 0;
	}
	~My_Heap()
	{
		delete[] pRoot;
		pRoot = nullptr;
		len = MaxLen = 0;
	}

	//往堆中插入元素
	void insert(const T& data);
	//遍历
	void travel()const;
	//删除堆顶
	T pop();
};

----------- 往堆中插入元素

我们采用 小顶堆的方式，即保证孩子节点要比父亲节点大。
采用动态内存分配的方法，插入一个节点到数组中。
从堆底开始，根据下标关系找到对应的父节点.

插入步骤：（小顶堆）

  1. 比较插入节点与当前父节点的关系
  2. 如果比父节点小，则当前节点需要上提，交换当前节点与父节点的值
  3. 如果比父节点大，则说明不冲突，则直接退出即可，因为经过以前的处理此情况一定是合法的。
  4. 继续比较，直到不冲突或者到达了根节点为止。

注意：我们使用自底向上的方式，每次比较当前节点与父节点的关系，然后需要将当前节点往上提，继续比较和上一层的关系

图例：
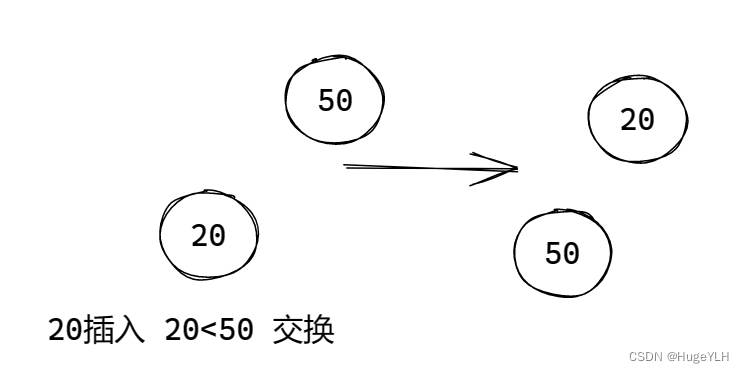
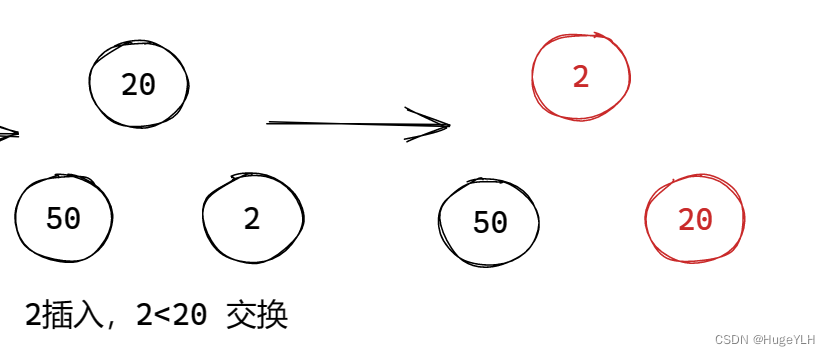
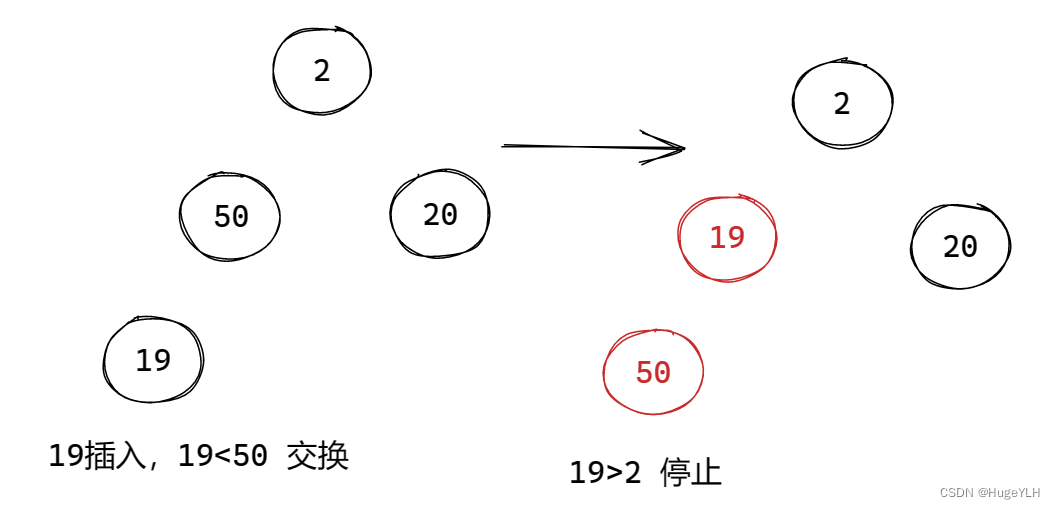
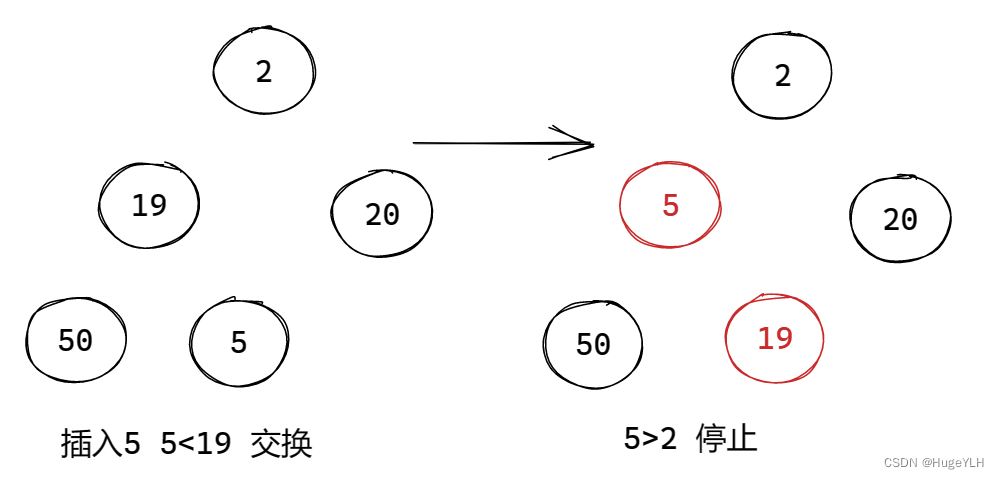
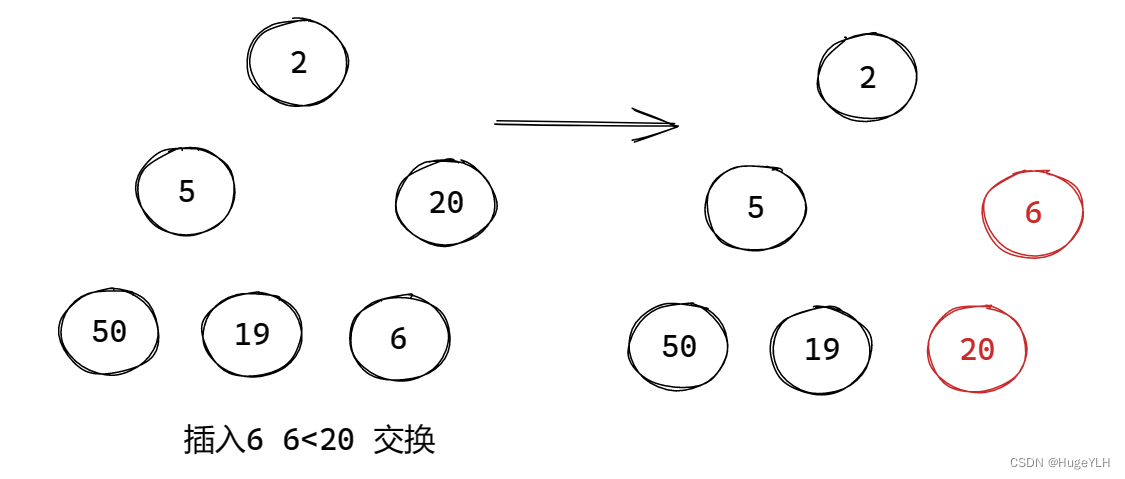
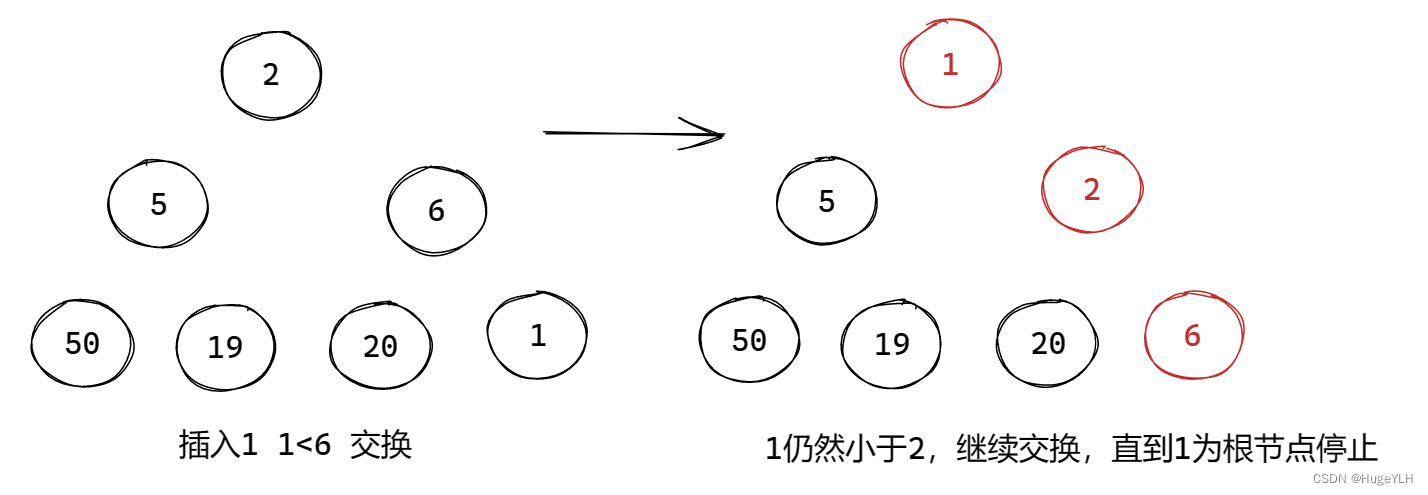
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

要点：从下往上遍历，交换不合适的节点。

template<class T>
inline void My_Heap<T>::insert(const T& data)
{
	//动态数组
	//1 像动态数组一样进来
	if (MaxLen <= len) {//需要申请
		//计算需要申请的内存大小   //>>1 右移一位 等同于除以2
		MaxLen = MaxLen + (((MaxLen >> 1) > 1) ? (MaxLen >> 1) : 1);
		//1 开内存
		T* pNew = new T[MaxLen];
		if (pRoot) {
			//2 pArr指向内存段中数据拷贝到pNew指向内存段
			memcpy(pNew, pRoot, sizeof(T) * len);
			//3 释放pArr指向内存段
			delete[] pRoot;
		}
		//4 pArr指向新开内存
		pRoot = pNew;
	}
	pRoot[len++] = data;

	//循环和父节点比较，如果冲突交换，不冲突，覆盖
	if (len == 1)
	{
		return;
	}
	int CurrentIdx= len - 1;				//孩子节点
	int ParentIdx = (CurrentIdx - 1) / 2;	//父节点
	T temp;
	while (1)
	{
		if (CurrentIdx <= 0)
			break;		//没有父节点，循环结束
		ParentIdx = (CurrentIdx - 1) / 2;
		if (pRoot[ParentIdx] < pRoot[CurrentIdx])
			break;	//不冲突，孩子父亲大，则停止
		//否则，交换元素
		temp = pRoot[ParentIdx];
		pRoot[ParentIdx] = pRoot[CurrentIdx];
		pRoot[CurrentIdx] = temp;
		//遍历完一次后，接着往上移动，开始重新一次比较
		CurrentIdx = ParentIdx;
	}
}

不使用动态内存分配：

void InsertData(int val)
	{
		arr[++this->size] = val;
		if (this->size == 1) return;
		int curLen = this->size;//当前节点
		int parentLen = curLen >> 1;//父节点
		while (true)
		{
			if (curLen <= 1) break;//到达根节点，退出
			//比较和父节点的关系，比父节点小则交换
			parentLen = curLen >> 1;
			if (arr[curLen] > arr[parentLen])
			{
				break;
			}
			swap(arr[curLen], arr[parentLen]);
			curLen = parentLen;
		}
	}

----------- 删除堆顶

从堆顶开始，把最后一个元素覆盖堆顶元素，接着根据下标关系，找到堆顶的孩子节点，比较两个孩子谁是最小孩子，如果堆顶比最小孩子节点小，则退出（小顶堆）。否则，交换两个节点，要保证父小于子。然后顶堆往下移动，移动到下一层的父节点，比较父子关系。确保在覆盖了原堆顶（即删除了原堆顶）后，整个堆结构仍然是以小堆顶的结构，因此要进行重排，直到数组下标越界为止。

步骤：

  1. 最后一个元素覆盖堆顶元素
  2. 当前节点寻找两个孩子节点的最小的那个，并且把那个最小的与当前节点的值作交换
  3. 当前节点下移，继续寻找最小的元素并且作交换
  4. 直到超过了下界之后停止。

注意：如果堆顶元素比左右孩子最小的元素都小，则不冲突，因此直接结束循环

图例：

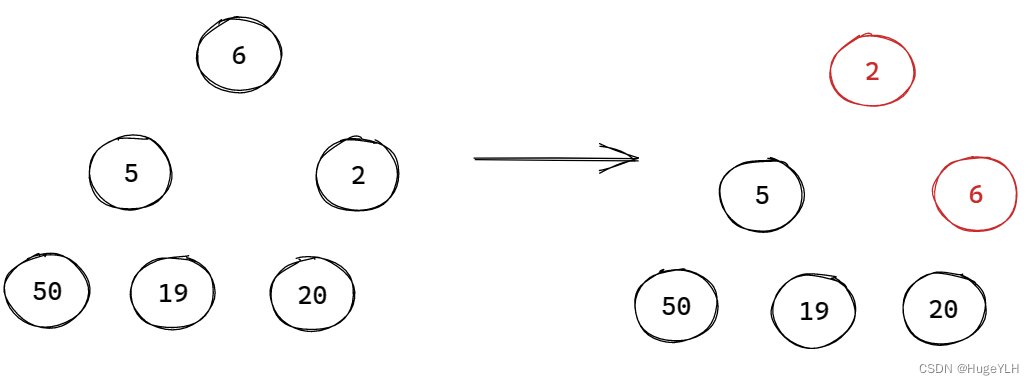
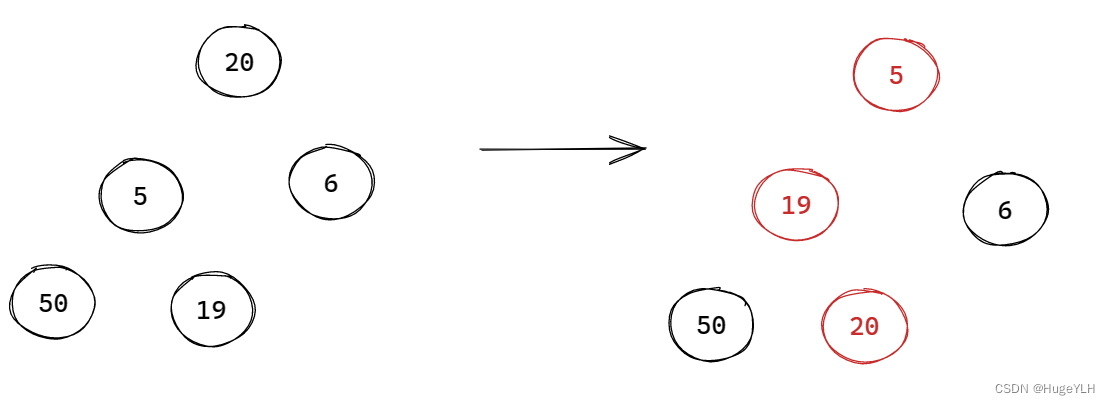
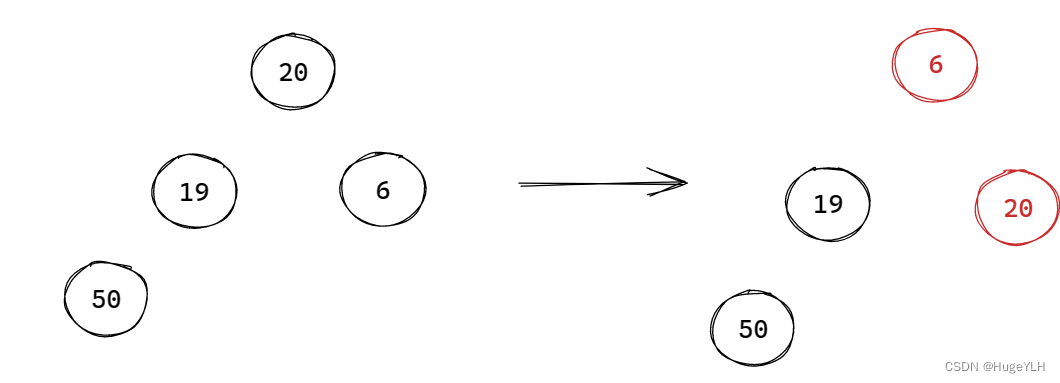
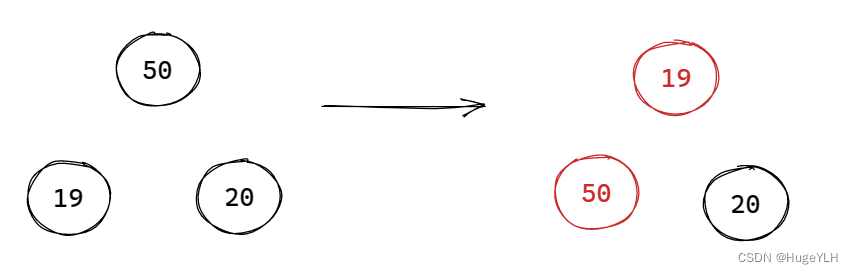
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

要点：从上往下遍历，重排堆结构的父子关系。

template <class T>
//删除堆顶
T MyHeap<T>::pop(){
	if (0 == len){
		cout << "堆为空，删除失败!" << endl;
		return (T)0;
	}//没法删
	if (1 == len){//只有一个
		len--;
		return pRoot[0];
	}
	//1 临时保存堆顶元素
	T temp = pRoot[0];
	//2 最后一个覆盖堆顶元素
	pRoot[0] = pRoot[len - 1];
	//3 循环  
	int currentIdx = 0;//从堆顶开始
	int minChildIdx;
	while (1){
		//数组结束 
		if ((currentIdx * 2 + 1) > (len - 1) ||
			(currentIdx * 2 + 2) > (len - 1)){
			break;
		}
		// 找到最小的孩子 
		minChildIdx = currentIdx * 2 + 1;//假定左孩子比较小
		//如果左孩子比右孩子大，右孩子最小
		if (pRoot[minChildIdx] > pRoot[minChildIdx + 1]) 
			minChildIdx++;
		//比最小孩子还小 循环结束
		if (pRoot[len-1] < pRoot[minChildIdx]) break;
		//当前位置和最小孩子交换 //子覆盖父
        //简单交换方式
        temp1 = pRoot[CurrentIdx];
		pRoot[CurrentIdx] = pRoot[MinChildIdx];
		pRoot[MinChildIdx] = temp1;
		//往下移动
		currentIdx = minChildIdx;
	}

	//4 返回
	len--;
	return temp;
}

不使用动态内存分配

int pop()
	{
		/*
		删除堆顶元素
		*/
		if (this->size == 1)
		{
			this->size = 0;
			return arr[1];
		}
		//1. 最后一个元素覆盖堆顶元素
		int temp = arr[1];
		arr[1] = arr[this->size];
		int curLen = 1;//当前节点
		int childLen = curLen << 1;//孩子节点
		while (true)
		{
			//下移超过了边界则退出
			if (((curLen << 1) > this->size) || (curLen << 1 | 1) > this->size)
			{
				break;
			}
			//找到两个孩子中最小的一个
			childLen = curLen << 1;//默认最小的是左孩子
			if (arr[childLen] > arr[childLen + 1])
			{
				childLen += 1;//最小的为右孩子
			}
			//堆顶比最小的孩子还小，则无需交换
			if (arr[this->size] < arr[childLen]) break;
			//交换当前节点与孩子节点的值
			swap(arr[childLen], arr[curLen]);
			curLen = childLen;//下移到孩子
		}
		this->size--;//最后总的个数要减一个
		return temp;
	}

堆排序构建

template <class T>
//直接用数组方式来构建堆
void MyHeap<T>::initHeap(T* pArr, int size){
	//开内存
	maxLen = size;
	len = 0;
	pRoot = new T[size];
	//数据进来
	pRoot[len++] = pArr[0];//第一个
	int currentIdx;
	int parentIdx;
	for (int i = 1; i < size; i++){
		currentIdx = len;
		parentIdx = (currentIdx - 1) / 2;


		//数据先放进来
		pRoot[currentIdx] = pArr[i];

		while (1){
			if (currentIdx <= 0) break;//没有父节点 循环结束
			parentIdx = (currentIdx - 1) / 2;
			if (pRoot[parentIdx] < pRoot[currentIdx]) break;

			//冲突 父节点覆盖子节点
			pRoot[currentIdx] = pRoot[parentIdx];
			//往上移
			currentIdx = parentIdx;
		}
		//新数据覆盖回来
		pRoot[currentIdx] = pArr[i];
		//个数增加
		len++;
	}
}

完整代码及测试

动态分配版本

在这里插入图片描述

#pragma once
#include <iostream>
using namespace std;
template <class T>
class My_Heap
{
private:
	T* pRoot;	//指向堆的指针，实际上是一个动态数组
	int len;	//元素个数
	int MaxLen;	//容量
public:
	My_Heap()
	{
		pRoot = nullptr;
		len = MaxLen = 0;
	}
	~My_Heap()
	{
		delete[] pRoot;
		pRoot = nullptr;
		len = MaxLen = 0;
	}

	//往堆中插入元素
	void insert(const T& data);
	//遍历
	void travel()const;
	//删除堆顶
	T pop();
	void initHeap(T* pArr, int size);
};

template<class T>
inline void My_Heap<T>::insert(const T& data)
{
	//动态数组
	//1 像动态数组一样进来
	if (MaxLen <= len) {//需要申请
		//计算需要申请的内存大小   //>>1 右移一位 等同于除以2
		MaxLen = MaxLen + (((MaxLen >> 1) > 1) ? (MaxLen >> 1) : 1);
		//1 开内存
		T* pNew = new T[MaxLen];
		if (pRoot) {
			//2 pArr指向内存段中数据拷贝到pNew指向内存段
			memcpy(pNew, pRoot, sizeof(T) * len);
			//3 释放pArr指向内存段
			delete[] pRoot;
		}
		//4 pArr指向新开内存
		pRoot = pNew;
	}
	pRoot[len++] = data;

	//循环和父节点比较，如果冲突交换，不冲突，覆盖
	if (len == 1)
	{
		return;
	}
	int CurrentIdx= len - 1;				//孩子节点
	int ParentIdx = (CurrentIdx - 1) / 2;	//父节点
	T temp;
	while (1)
	{
		if (CurrentIdx <= 0)
			break;		//没有父节点，循环结束
		ParentIdx = (CurrentIdx - 1) / 2;
		if (pRoot[ParentIdx] < pRoot[CurrentIdx])
			break;	//不冲突，循环继续
		//效率较低
		temp = pRoot[ParentIdx];
		pRoot[ParentIdx] = pRoot[CurrentIdx];
		pRoot[CurrentIdx] = temp;
		//往上移动
		CurrentIdx = ParentIdx;
	}
}

template<class T>
inline void My_Heap<T>::travel() const
{
	for (int i = 0; i < len; i++)
	{
		cout << pRoot[i] << " ";
	}
	cout << endl;
}

template<class T>
inline T My_Heap<T>::pop()
{
	if (len == 0)
	{
		cout << "堆为空!\n";
		return (T)0;
	}
	if (len == 1)
	{
		len--;	//只有一个元素
		return pRoot[0];
	}

	//1. 临时保存堆顶元素
	T temp = pRoot[0];
	T temp1;
	//2. 最后一个元素覆盖堆顶元素
	pRoot[0] = pRoot[len - 1];

	//从堆顶开始
	int CurrentIdx = 0;
	int MinChildIdx;
	while (1)
	{
		//越界
		if ((CurrentIdx * 2 + 1) > (len - 1) ||
			(CurrentIdx * 2 + 2) > (len - 1))
		{
			break;
		}
		//找到最小孩子
		//先假设左孩子比较小
		MinChildIdx = CurrentIdx * 2 + 1;
		if (pRoot[MinChildIdx] > pRoot[MinChildIdx + 1])
		{
			MinChildIdx++;	//右孩子比较小
		}
		//如果比最小孩子还小
		if (pRoot[len-1] < pRoot[MinChildIdx])
			break;
		//需要交换，采用简单交换, 子覆盖父
		temp1 = pRoot[CurrentIdx];
		pRoot[CurrentIdx] = pRoot[MinChildIdx];
		pRoot[MinChildIdx] = temp1;
		//父节点往下移动
		CurrentIdx = MinChildIdx;
	}

	len--;
	return temp;
}

template <class T>
//直接用数组方式来构建堆
void My_Heap<T>::initHeap(T* pArr, int size) {
	//开内存
	MaxLen = size;
	len = 0;
	pRoot = new T[size];
	//数据进来
	pRoot[len++] = pArr[0];//第一个
	int currentIdx;
	int parentIdx;
	for (int i = 1; i < size; i++) {
		currentIdx = len;
		parentIdx = (currentIdx - 1) / 2;


		//数据先放进来
		pRoot[currentIdx] = pArr[i];

		while (1) {
			if (currentIdx <= 0) break;//没有父节点 循环结束
			parentIdx = (currentIdx - 1) / 2;
			if (pRoot[parentIdx] < pRoot[currentIdx]) break;

			//冲突 父节点覆盖子节点
			pRoot[currentIdx] = pRoot[parentIdx];
			//往上移
			currentIdx = parentIdx;
		}
		//新数据覆盖回来
		pRoot[currentIdx] = pArr[i];
		//个数增加
		len++;
	}
}

#include "MyHeap.h"

#define NUM 11
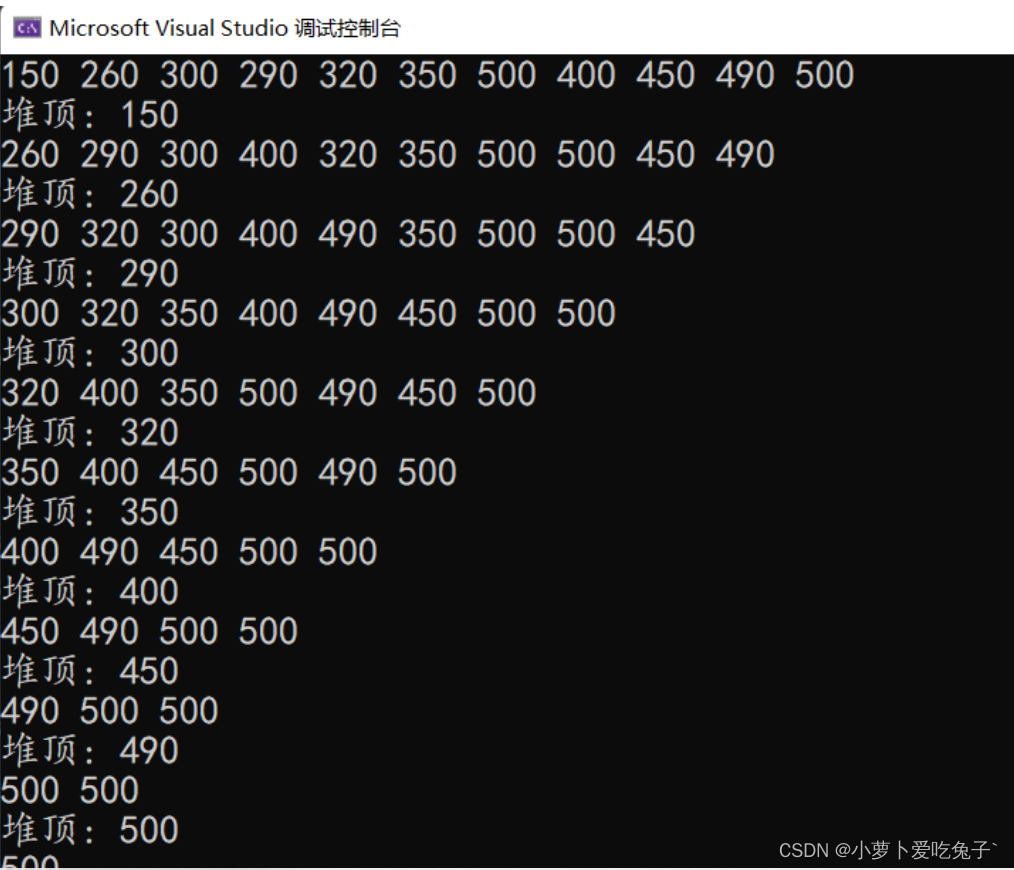
int main()
{
	int arr[NUM] = { 150,260,300,290,320,350,500,400,450,490,500 };
	My_Heap<int> a;

	/*for (int i = 0; i < NUM; i++)
	{
		a.insert(arr[i]);
		a.travel();
	}*/
	a.initHeap(arr, NUM);
	a.travel();
	return 0;
}

非动态版本

P1177 【模板】快速排序 ----排序测试

Ac code

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
using namespace std;
#define int long long
const int N = 1e5 + 10;
const int CurSize = 1e5 + 10;
struct Tree
{
	int arr[N];
	int size;
	Tree() { memset(arr, 0, sizeof(arr)); size = 0; }
	void InsertData(int val)
	{
		arr[++this->size] = val;
		if (this->size == 1) return;
		int curLen = this->size;//当前节点
		int parentLen = curLen >> 1;//父节点
		while (true)
		{
			if (curLen <= 1) break;//到达根节点，退出
			//比较和父节点的关系，比父节点小则交换
			parentLen = curLen >> 1;
			if (arr[curLen] > arr[parentLen])
			{
				break;
			}
			swap(arr[curLen], arr[parentLen]);
			curLen = parentLen;
		}
	}
	int pop()
	{
		/*
		删除堆顶元素
		*/
		if (this->size == 1)
		{
			this->size = 0;
			return arr[1];
		}
		//1. 最后一个元素覆盖堆顶元素
		int temp = arr[1];
		arr[1] = arr[this->size];
		int curLen = 1;//当前节点
		int childLen = curLen << 1;//孩子节点
		while (true)
		{
			//下移超过了边界则退出
			if (((curLen << 1) > this->size) || (curLen << 1 | 1) > this->size)
			{
				break;
			}
			//找到两个孩子中最小的一个
			childLen = curLen << 1;//默认最小的是左孩子
			if (arr[childLen] > arr[childLen + 1])
			{
				childLen += 1;//最小的为右孩子
			}
			//堆顶比最小的孩子还小，则无需交换
			if (arr[this->size] < arr[childLen]) break;
			//交换当前节点与孩子节点的值
			swap(arr[childLen], arr[curLen]);
			curLen = childLen;//下移到孩子
		}
		this->size--;//最后总的个数要减一个
		return temp;
	}
};
signed main()
{
	Tree t;
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		int p;
		cin >> p;
		t.InsertData(p);
	}
	while (t.size != 0)
	{
		cout << t.pop() << " ";
	}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/363513.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

sql join、left join、full join的区别总结，注意事项

sql join、left join、full join的区别总结，注意事项

1. 结论图 见 https://www.runoob.com/sql/sql-join.html 2. 测试 2.1. 造数据 数据表 mysql脚本 DROP TABLE IF EXISTS class; CREATE TABLE class (c_id INTEGER NOT NULL COMMENT 班级ID,c_name VARCHAR(100) NOT NULL COMMENT 班级名,PRIMARY KEY (c_id) ) CO…
阅读更多...
JavaEE简单示例——动态SQL的复杂查询操作＜foreach＞

JavaEE简单示例——动态SQL的复杂查询操作＜foreach＞

简单介绍&#xff1a; 在我们之前学习MySQL的时候&#xff0c;我们曾经有一个操作叫做查询区间&#xff0c;比如我们使用in关键字查询id为3到6之间的值&#xff0c;或者查询id小于100的值&#xff0c;这时候如果将SQL语句一条一条的查询出来进行筛选效率就太慢了&#xff0c;所…
阅读更多...
【05-JVM面试专题-运行时数据区的结构都有哪些？哪些是共享的呢？哪些是非共享的呢？详细的介绍一下运行时数据区结构各部分的作用？】

【05-JVM面试专题-运行时数据区的结构都有哪些？哪些是共享的呢？哪些是非共享的呢？详细的介绍一下运行时数据区结构各部分的作用？】

运行时数据区的结构都有哪些&#xff1f;哪些是共享的呢&#xff1f;哪些是非共享的呢&#xff1f;详细的介绍一下运行时数据区结构各部分的作用&#xff1f; 运行时数据区的结构都有哪些&#xff1f;哪些是共享的呢&#xff1f;哪些是非共享的呢&#xff1f;详细的介绍一下运行…
阅读更多...
带您了解TiDB MySQL数据库中关于日期、时间的坑

带您了解TiDB MySQL数据库中关于日期、时间的坑

带您了解TiDB & MySQL数据库中关于日期、时间的坑时间的基础知识什么是时间计算时间的几种方法世界时&#xff08;UT&#xff09;协调世界时&#xff08;UTC&#xff09;国际原子时&#xff08;TAI&#xff09;时区的概念中国所在的时区操作系统的时区datetimedatectl数据库…
阅读更多...
Spring代理模式——静态代理和动态代理

Spring代理模式——静态代理和动态代理

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…
阅读更多...
python打包exe实用工具auto-py-to-exe的操作方法

python打包exe实用工具auto-py-to-exe的操作方法

auto-py-to-exe操作方法auto-py-to-exe 是一个用于打包 python 程序的程序。本文就是主要介绍如何使用 auto-py-to-exe 完成 python 程序打包。本文主要分为两节&#xff0c;第一节主要对 auto-py-to-exe 做一些介绍&#xff0c;第二节则是演示 auto-py-to-exe 的打包过程。一、…
阅读更多...
pygraphviz安装教程

pygraphviz安装教程

0x01. 背景 最近在做casual inference&#xff0c;做实验时候想因果图可视化&#xff0c;遂需要安装pygraphviz&#xff0c;整了一下午&#xff0c;终于捣鼓好了&#xff0c;真头大。 环境&#xff1a; win10操作系统python3.9环境 0x02. 安装Graphviz 传送门&#xff1a;…
阅读更多...
linux:本地套接字通信客户和服务器代码

linux:本地套接字通信客户和服务器代码

客户端代码 #include <stdlib.h> #include <stdio.h> #include <unistd.h> #include <sys/types.h> #include <sys/stat.h> #include <string.h> #include <arpa/inet.h> #include <sys/un.h> int main(int argc, const cha…
阅读更多...
中间件安全—Tomcat常见漏洞

中间件安全—Tomcat常见漏洞

中间件安全—Tomcat常见漏洞1.Tomcat常见漏洞1.1.前言1.2.文件上传 (CVE-2017-12615)1.2.1.漏洞原理1.2.2.影响版本1.2.3.漏洞复现1.2.3.1.测试是否允许PUT1.2.3.2.验证漏洞是否存在1.2.3.3.访问test.jsp1.2.3.4.上传执行命令脚本1.2.3.5.执行命令1.3.文件包含漏洞&#xff08;…
阅读更多...
【第一章 - 绪论】- 数据结构（近八千字详解）

【第一章 - 绪论】- 数据结构（近八千字详解）

目录 一、 数据结构的研究内容 二、基本概念和术语 2.1 - 数据、数据元素、数据项和数据对象 2.2 - 数据结构 2.2.1 - 逻辑结构 2.2.2 - 存储结构 2.3 - 数据类型和抽象数据类型 三、抽象数据类型的表现与实现 四、算法和算法分析 4.1 - 算法的定义及特性 4.2 - 评价…
阅读更多...
手把手教大家在 gRPC 中使用 JWT 完成身份校验

手把手教大家在 gRPC 中使用 JWT 完成身份校验

文章目录1. JWT 介绍1.1 无状态登录1.1.1 什么是有状态1.1.2 什么是无状态1.2 如何实现无状态1.3 JWT1.3.1 简介1.3.2 JWT数据格式1.3.3 JWT 交互流程1.3.4 JWT 存在的问题2. 实践2.1 项目创建2.2 grpc_api2.3 grpc_server2.4 grpc_client3. 小结上篇文章松哥和小伙伴们聊了在 …
阅读更多...
Docker 如何配置镜像加速

Docker 如何配置镜像加速

Docker 镜像加速 国内从 DockerHub 拉取镜像有时会遇到困难&#xff0c;此时可以配置镜像加速器。Docker 官方和国内很多云服务商都提供了国内加速器服务&#xff0c;例如&#xff1a; 科大镜像&#xff1a;https://docker.mirrors.ustc.edu.cn/网易&#xff1a;https://hub-…
阅读更多...
生态流量数据采集传输协议定制开发(嵌入式水资源SZY206协议以及VC++ POST数据发送)

生态流量数据采集传输协议定制开发(嵌入式水资源SZY206协议以及VC++ POST数据发送)

水电站生态流量在线监测&#xff0c;流量数据采集传输,水资源遥测终端机程序。 背景&#xff1a;现场使用SCJ-LL01多普勒超声波流量计采集生态下泄流量&#xff0c;使用太阳能供电系统&#xff0c;使用SCJ-RTU01遥测终端机进行数据采集&#xff0c;设备采用4G通讯&#xff0c;…
阅读更多...
基于MATLAB开发AUTOSAR软件应用层模块-part23.SR interface通信介绍（接收的数据错误时应该如何处理）

基于MATLAB开发AUTOSAR软件应用层模块-part23.SR interface通信介绍（接收的数据错误时应该如何处理）

在软件SWC之间的AUTOSAR SR通信中，当COM报告接收SWC的数据接收错误时，运行时环境（RTE）触发DataReceiveErrorEvent。该事件可以指示发送方SWC未能在AliveTimeout限制内回复，或者发送方SWC发送了无效数据。 接下来我们就讲解下怎么实现无效数据的接收和判断 还是三步走，建模…
阅读更多...
Ubuntu 上 Let‘s Encrypt 生成泛域名证书

Ubuntu 上 Let‘s Encrypt 生成泛域名证书

安装生成工具certbot&#xff1a; apt install certbot 查看安装在哪&#xff1a; which certbot 使用certbot&#xff08;位置在 /usr/bin/certbot&#xff09;生成证书&#xff1a; /usr/bin/certbot certonly -d *.xxx.com --manual --preferred-challenges dns --ser…
阅读更多...
一种全新的图像滤波理论的实验（二）

一种全新的图像滤波理论的实验（二）

一、前言 2021年12月31日&#xff0c;我发布了基于加权概率模型的图像滤波算法的第一个实验&#xff0c;当时有两个关键问题没有解决&#xff1a; 1、出现了大面积的黑色区域&#xff0c;最近考虑把这个算法实际应用在图像和视频的压缩领域&#xff0c;于是通过对程序的分析&a…
阅读更多...
【论文简述】GMFlow: Learning Optical Flow via Global Matching（CVPR 2022）

【论文简述】GMFlow: Learning Optical Flow via Global Matching（CVPR 2022）

一、论文简述 1. 第一作者&#xff1a;Haofei Xu 2. 发表年份&#xff1a;2022 3. 发表期刊&#xff1a;CVPR oral 4. 关键词&#xff1a;光流、代价体、Transformers、全局匹配、注意力机制 5. 探索动机&#xff1a;过去几年中具有代表性的光流学习框架的核心估计方式没有…
阅读更多...
Java文件IO及其案例分析

Java文件IO及其案例分析

目录 1. 文件概述 1.1 狭义和广义上的文件 1.2 文件的路径 1.3 文件的类型 2. 针对文件系统的操作 3. 针对文件内容的操作&#xff08;文件的读和写&#xff09; 3.1 IO流对象 3.2 文件的读操作&#xff08;字节流&#xff09; 3.3 文件的写操作&#xff08;字节流&#…
阅读更多...
内存取证常见例题思路方法-volatility (没有最全 只有更全)

内存取证常见例题思路方法-volatility (没有最全 只有更全)

目录 1.从内存文件中获取到用户hacker 的密码并且破解密码&#xff0c;将破解后的密码作为 Flag值提交; 2.获取当前系统的主机名&#xff0c;将主机名作为Flag值提交; 3.获取当前系统浏览器搜索过的关键词&#xff0c;作为Flag提交; 4.获取当前内存文件的 ip地址 5.当前系…
阅读更多...
pycharm和navigator打开时出现报错，无法正常打开

pycharm和navigator打开时出现报错，无法正常打开

1、navigator打开时出现提示&#xff1a; 原因是&#xff1a;python.exe有多个任务在占用。 解决办法&#xff1a; &#xff08;1&#xff09;打开cmd &#xff08;2&#xff09;输入&#xff1a;tasklist | findstr “pythonw” &#xff08;3&#xff09;有几个线程就kill几个…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023