这一节进入正定矩阵的内容，什么叫做正定矩阵？为什么我们对矩阵正定这么感兴趣？

PS：这一节将前面所有的概念都融合在一起：主元、行列式、特征值、不稳定性

一、正定矩阵的判断方法

为了说明问题，我们先考虑二阶矩阵$A$
$$A=\left[\begin{array}{cc}a& b\\ b& c\end{array}\right]$$

• 特征值判断法 ${\lambda }_1>0$ ${\lambda }_2>0$；
• 行列式判断法 $a>0$ $ac-b^2>0$；
• 主元判断法 $a>0$ $\frac{ac-b^2}{a}>0$；
• 判断式 $x^{T}Ax>0$；

PS：线性代数范围内，正定矩阵需要是对称矩阵。

例子：
$$\left[\begin{array}{cc}2& 6\\ 6& ?\end{array}\right]$$
填入什么数字会使得其为正定矩阵？

• 填入数字18，该矩阵行列式恰好为0，矩阵称为半正定；
• 填入大于18的数字，矩阵行列式顺序主子式均为正数

OK！为什么正定对于我们线性代数非常重要？因为它与工程联系非常密切，切入点就是最后一个判断正定的条件$x^{T}Ax>0$。

对于半正定矩阵$A=\left[\begin{array}{cc}2& 6\\ 6& 18\end{array}\right]$，我们写出其计算式$x^{T}Ax$：
$$x^{T}Ax=\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]\left[\begin{array}{cc}2& 6\\ 6& 18\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=2x_1^2+12x_1{x}_2+18x_2^2$$
对上述的式子进行配方：
$$\begin{array}{rl}z& =a{x}_1^2+2b{x}_1{x}_2+c{x}_2^2\\ & =2x_1^2+12x_1{x}_2+18x_2^2=2(x_1+3x_2{)}^2\end{array}$$
我们知道 $Ax$ 是线性的，但是左乘了一个$x^T$就变成了二阶的，这种形式称为二次型形式 （Quadratic From），它是“纯” 二次形式的，没有线性部分，常数项和3、4或者其他次方。给出正定矩阵的定义，对于任何$x_1,x_2$所有值都大于零。

无论$x_1,x_2$如何取值，对应的结果均大于零。如何研究这个曲线的形状，一种可行的方法就是截面法，通过固定其中的一个值，然后研究其形状，最后在将固定的值进行遍历就能大概知道这个曲线的形状了。

通过配方，固定 $x_1$ 可以看出 $z=2(x_0+3x_2{)}^2$，它是一个抛物线且顶点坐标为：
$$x_2=-\frac{1}{3}{x}_0$$
从与 $x$ 垂直的截面来看，它首先是一个抛物线，随着 $x_1$ 的增加，对称轴坐标$x_2$逐渐减少。从$X$轴上截面看就好像一个不断平移的抛物线。同理，如果固定 $x_2$ 研究这个界面，也是一个不断平移的抛物面。

二、正定矩阵与空间曲线草图

考察一个对称矩阵：
$$A=\left[\begin{array}{cc}2& 6\\ 6& ?\end{array}\right]$$
在问号中填入不同的数字，矩阵可能满足正定，也可能是非正定的，甚至有可能是半正定。现在的问题是，正定性与其对应的二次型曲线有什么关系？满足正定是怎么样得到？不满足的又是何种情况？

OK！假如问号中的数字是20，对称矩阵变成：
$$A=\left[\begin{array}{cc}2& 6\\ 6& 20\end{array}\right]$$
对于二阶矩阵最简单的方式就是通过从左上到左下行列式，显然分别是2和4都是大于零的，所以矩阵 $A$ 是正定的。因为我们需要研究的是对应二次型的空间曲线，所以先将其写成二次型：
$$x^{T}Ax=\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]\left[\begin{array}{cc}2& 6\\ 6& 20\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=2x_1^2+12x_1{x}_2+20x_2^2$$
为了在直角坐标系中表示，将方程写成我们熟悉的形式：
$$z=2x^2+12xy+20y^2$$
不妨从特殊点着手，首先方程过 $(0,0,0)$ 点、$(1,0,2)$：

用一个平行于 $XOY$ 且过原点平面去截取这个曲面：
$$\begin{array}{rl}z& =2x^2+12xy+20y^2\\ 0& =x_{0}x\end{array}$$
联立上述式子，有：
$$z=20y^2$$

再用 $x-y=0$ 平面去截取这个曲面：
$$\begin{array}{rl}z& =2x^2+12xy+20y^2\\ x-y& =0\end{array}$$
联立得：
$$z=34y^2$$

不过，现代软件可以很轻松帮你绘制这样的图形：

所谓正定，就是这个曲线所有的高度值都是大于零的。

再来看一个非正定的矩阵对应的二次曲线：
$$\left[\begin{array}{cc}2& 6\\ 6& 2\end{array}\right]$$

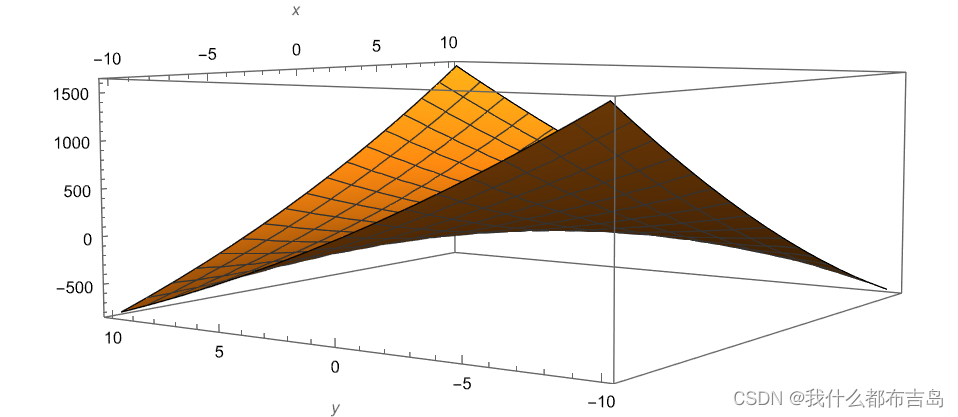
有部分的值是负数，所以不是正定的。