LeetCode 73. 矩阵置零

难度：$middle$

---

题目描述

给定一个 KaTeX parse error: Double subscript at position 3: _m_̲ x _n_ 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法 。

示例 1：

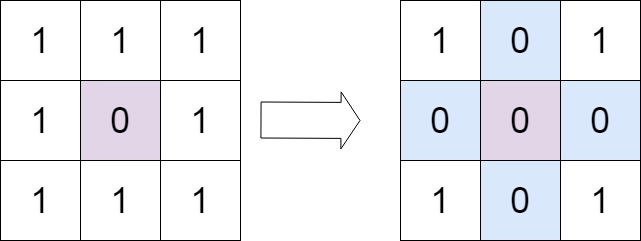
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• $m==matrix.length$
• $n==matrix[0].length$
• $1<=m,n<=200$
• $-2^{31}<=matrix[i][j]<=2^{31}-1$

进阶：

• 一个直观的解决方案是使用 $O(mn)$ 的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用 $O(m+n)$ 的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗？

---

算法

(原地算法) $O(nm)$

我们只需统计出矩阵中每一行或者每一列是否有0，然后把含有0的行或者列都置成0即可。

• 用两个变量记录第一行和第一列是否有0。
• 遍历整个矩阵，用矩阵的第一行和第一列记录对应的行和列是否有0。
• 把含有0的行和列都置成0。

复杂度分析

• 时间复杂度：矩阵中每个元素只遍历常数次数，所以时间复杂度是$O(nm)$。

• 空间复杂度 : 只用了两个额外的变量记录第一行和第一列是否含有0，所以额外的空间复杂度是 $O(1)$。

C++ 代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        if (matrix.empty()) return;
        int n = matrix.size(), m = matrix[0].size();

        int r0 = 1, c0 = 1;
        //判断第0行
        for (int i = 0; i < m; i ++) if (matrix[0][i] == 0) r0 = 0;
        //判断第0列
        for (int i = 0; i < n; i ++) if (matrix[i][0] == 0) c0 = 0;

        //判断第1行到第n - 1行是否有0，存储在第一列中
        for (int i = 1; i < n; i ++) {
            for (int j = 0; j < m; j ++) {
                if (matrix[i][j] == 0) matrix[i][0] = 0;
            }
        }

        //判断第1列到第 n - 1列是否有0，存储在第一行中
        for (int i = 1; i < m; i ++) {
            for (int j = 0; j < n; j ++) {
                if (matrix[j][i] == 0) matrix[0][i] = 0;
            }
        }

        // 修改行的数值
        for (int i = 1; i < n; i ++ ) {
            if (matrix[i][0] == 0) 
                for (int j = 0; j < m; j ++) 
                    matrix[i][j] = 0;
        }

        //修改列的数值
        for (int i = 1; i < m; i ++) {
            if (matrix[0][i] == 0) 
                for (int j = 0; j < n; j ++)
                    matrix[j][i] = 0;
        }

        //修改第一行
        if (r0 == 0) for (int i = 0; i < m; i ++) matrix[0][i] = 0;
        //修改第一列
        if (c0 == 0) for (int i = 0; i < n; i ++) matrix[i][0] = 0;
        
    }
};

---