文章目录
- 4 插入
- 4.1 序
- 4.2 向单个2-结点插入新键
- 4.3 向树底部的2-结点插入新键
- 4.4 向一棵双键树(3-结点)中插入新键
- 4.5 颜色调整
- 4.6 根结点总是黑色
- 4.7 向树底部的3-结点插入新键
- 4.8 将红链接在树中向上传递
- 4.9 实现
- 5 删除
- 5.1 删除最小键
- 5.2 删除
- 6 有序性相关方法
- 6.1 floor(),ceiling()
- 6.2 rank()
- 6.3 keys()
- 后记
4 插入
4.1 序
在插入新键时我们可以使用旋转操作帮助我们保证2-3树和红黑树直接的一一对应关系,因为旋转操作可以保持红黑树的两个重要性质:有序性和完美平衡性。下面讲解如何使用旋转操作保持红黑树的另外两个重要性质:不存在两条连续的红色链接和不存在红色的右链接。简单情况热身。
4.2 向单个2-结点插入新键
一棵只含有一个键的红黑树只含有一个2-结点。插入一个新键,如果新键小于老键,我们只需新增一个红色左子结点;如果新键大于老键,那么新增的红色结点形成一条红色的右链接。通过root=rotateLeft(root),将其旋转为红色的左链接,插入操作完成。两种情况的结果均为一棵和单个3-结点等价的红黑树,树的黑链高度1。如下图所示:
4.3 向树底部的2-结点插入新键
用和二叉查找树相同的方式向一棵红黑树中插入一个新键会在树的底部新增一个结点(保证有序性),新插入的结点链接总是红色。如果它的父链接是2-结点,情况同上。
4.4 向一棵双键树(3-结点)中插入新键
这种情况分为3种子情况:新键小于树中的2个键,在两者之间,或者大于两者。每种情况都会产生一个链接到两条红色链接的结点,需要调整:
- 最简单的情况新键大于原树中的两个键,新键被连接到3-结点的右链接。此时树是平衡的,根结点为中间大小的键,它有两条红链接分别和较小和较大的结点相连。此时我们只需要把两条链接颜色有红变黑,得到一棵由3个结点组成、高为2的平衡树。
- 新键小于原树中的两个键,它被链接到最左边的空链接,产出两条连续的红链接。此时将上层的红链接右旋,得到第一种情况。
- 新键介于原树中的两个键之间,它被连接到较小结点的右链接。此时先通过较小结点左旋,形成第二种情况。
图示如下: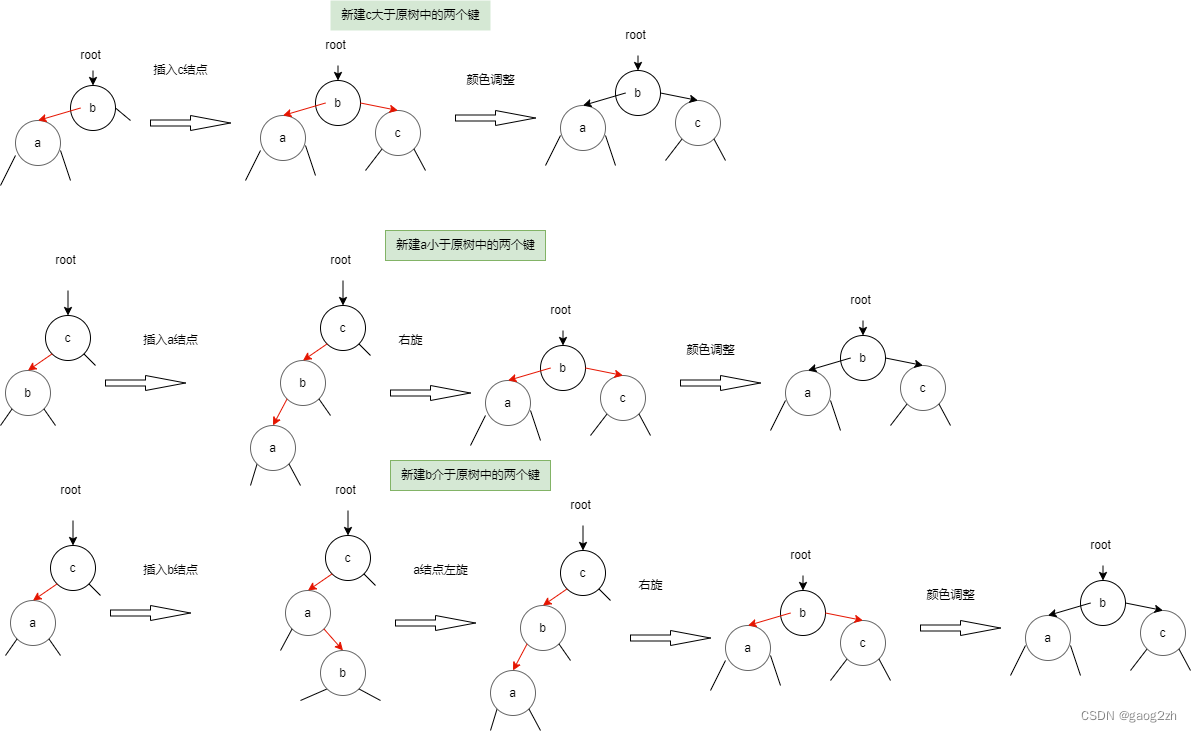
4.5 颜色调整
我们通过flipColor()方法来转换一个结点两个红色子节点的颜色。把两个子节点由红变黑,同时把父结点由黑变红。该操作是局部变换,不会影响整棵树的黑色平衡性。flipColor()源代码如下:
/**
* 变化双子链接为红色为黑色,红色转义到父结点
* @param p 当前结点
*/
private void flipColors(Node p) {
p.color = !p.color;
p.left.color = !p.left.color;
p.right.color = !p.right.color;
}
4.6 根结点总是黑色
上述颜色调整,根结点由黑变红,因此我们每次插入后都需要显示把根结点设为黑色。当根结点有红变黑时,树的黑脸高度+1。
4.7 向树底部的3-结点插入新键
现在假设我们需要在树的底部的一个3-结点下加入一个新结点。前面讨论的3种情况都会出现。颜色转换会使到中结点的链接变红,相当于把它送入父结点。这意味着父结点插入一个新键,继续用相同的办法解决这个问题。
4.8 将红链接在树中向上传递
插入算法的关键步骤:要在一个3-结点下插入新键,先创建一个临时的4-结点,将其分解并将红链接由中间键传递给它的父结点。重复这个过程,知道遇到一个2-结点或者根结点。
4.9 实现
插入给递归实现如下:
/**
* 插入键值对
* @param key 键
* @param value 值
*/
@Override
public void put(K key, V value) {
// 树为空
if (root == null) {
root = new Node(key, value);
return;
}
// 查找key是否在树中,且记录访问路径
Stack<Node> stack = new Stack<>();
Node cur = root;
Node p = null;
int type = 0;
while (cur != null) {
stack.push(cur);
p = cur;
int cmp = key.compareTo(cur.key);
if (cmp < 0) {
cur = cur.left;
type = 1;
} else if (cmp > 0) {
cur = cur.right;
type = 2;
} else {
cur.value = value;
return;
}
}
// key不在树中
Node n = new Node(key, value);
if (type == 1) {
// 新结点为左子结点
p.left = n;
} else {
// 新结点为右子结点
p.right = n;
}
// 插入新结点后,为满足红黑树性质沿遍历路径自下向上做平衡调整
// boolean ajusted = false;
while (!stack.isEmpty()) {
// ajusted = false;
cur = stack.pop();
cur.n += 1;
// 如果右链接为红色且左链接为黑色,则左旋
if (isRed(cur.right) && !isRed(cur.left)) {
// ajusted = true;
if (cur == root) {
root = cur = rotateLeft(cur);
} else {
p = stack.peek();
if (p.left == cur) {
p.left = cur = rotateLeft(cur);
} else {
p.right = cur = rotateLeft(cur);
}
}
}
// 如果左链接和左链接的左链接都为红色,则右旋
if (isRed(cur.left) && isRed(cur.left.left)) {
// ajusted = true;
if (cur == root) {
root = cur = rotateRight(cur);
} else {
p = stack.peek();
if (p.left == cur) {
p.left = cur = rotateRight(cur);
} else {
p.right = cur = rotateRight(cur);
}
}
}
// 如果左右链接都为红色,则把红色转移到父链接
if (isRed(cur.left) && isRed(cur.right)) {
// ajusted = true;
flipColors(cur);
}
// // 如果当前没做调整,那么它的祖先结点也无需调整
// if (!ajusted) {
// break;
// }
}
// 剩余祖先结点计数计算
// for (Node node : stack) {
// node.n++;
// }
// 保证根结点为黑色
root.color = BLACK;
}
5 删除
5.1 删除最小键
从树底部的3-结点删除键很简单,但是2-结点删除后,一般会替换为空链接,会破坏树的完美平衡性。所以为了确保不会删除一个2-结点,在沿着左链接向下过程中:
- 如果当前结点的左子结点不是2-结点,完成
- 如果当前结点是2-结点而它的亲兄弟结点不是2-结点,把左子结点的兄弟结点中的一个键移动到左子结点中
- 如果当前结点的左子结点和它的亲兄弟结点都是2-结点,将左子结点、父结点中的最小键和左子结点最近的兄弟结点合并为一个4-结点
在遍历完成后,最后得到一个含有最小键的3-结点或者4-结点,直接删除。然后在回头向上分解所有的4-结点。
非递归代码如下:
/**
* 删除最小结点
* @return 最小结点对应的value
*/
public void deleteMin() {
if (isEmpty()) {
throw new NoSuchElementException("BST underflow");
}
// 如果根结点左右链接都为黑色,变为4-结点
if (!isRed(root.left) && !isRed(root.right)) {
root.color = RED;
}
root = deleteMin(root);
if (!isEmpty()) {
root.color = BLACK;
}
}
/**
* 删除以p为根结点的树中最小结点
* @param p 根结点
* @return 删除最小结点后的新树
*/
private Node deleteMin(Node p) {
// 目标结点的左子树
Node pl;
// 目标结点的父结点
Node pp = null;
// 栈记录遍历结点(路径),用于删除后自下向上调整红黑树,以满足红黑树的性质
Stack<Node> stack = new Stack<>();
while ((pl = p.left) != null) {
// 如果左链接为2-结点,从兄弟结点或者父结点借
if (!isRed(pl) && !isRed(pl.left)) {
p = moveRedLeft(p);
if (pp != null) {
pp.left = p;
}
}
// 记录遍历结点
stack.push(p);
// 继续沿左子树遍历
pp = p;
p = pp.left;
}
// pp为空说明要删除的为根结点
if (pp == null) {
return null;
} else {
// 要删除的结点为非根结点,父结点的左链接置空
pp.left = null;
}
// 调整删除结点后的二叉树,以满足红黑树的性质
while (!stack.isEmpty()) {
p = stack.pop();
p.n--;
if (!stack.isEmpty()) {
stack.peek().left = balance(p);
} else {
return balance(p);
}
}
return null;
}
5.2 删除
在查找路径上进行和删除最小键相同的变换,可以保证在查找过程中任意当前结点不是2-结点。如果被查找的键在树的底部,可以直接删除;如果不在,我们需要把它和它的后继结点交换,问题转换为在一棵根结点不是2-结点的子树中删除最小的键。
非递归代码如下:
/**
* 删除指定的key
* @param key 指定key
*/
public void delete(K key) {
if (key == null) {
throw new IllegalArgumentException("argument to delete() is null");
}
if (!contains(key)) {
return;
}
// if both children of root are black, set root to red
if (!isRed(root.left) && !isRed(root.right)) {
root.color = RED;
}
root = delete(root, key);
if (!isEmpty()) {
root.color = BLACK;
}
}
/**
* 在以h为根结点的树中删除指定key
* @param h 树的根结点
* @param key key
* @return 删除后调整完的新树
*/
private Node delete(Node h, K key) {
// assert get(h, key) != null;
// 存储遍历的结点
Stack<Node> stack = new Stack<>();
Node t;
Node pp = null;
while (true) {
if (key.compareTo(h.key) < 0) {
// 比当前结点key小,确保当前结点不为2-结点
if (!isRed(h.left) && !isRed(h.left.left)) {
// 当前结点为2-结点,从兄弟结点借一个结点
t = moveRedLeft(h);
if (pp != null) {
adjustParentLink(h, pp, t);
}
h = t;
}
stack.push(h);
// 继续遍历左子树
pp = h;
h = h.left;
} else {
if (isRed(h.left)) {
t = rotateRight(h);
if (pp != null) {
adjustParentLink(h, pp, t);
}
h = t;
}
if (key.compareTo(h.key) == 0 && (h.right == null)) {
// 命中叶子结点
if (stack.isEmpty()) {
// 要删除的为根结点
return null;
} else {
// 非根结点,父链接置空
Node p = stack.peek();
if (p.left == h) {
p.left = null;
} else {
p.right = null;
}
}
break;
}
if (!isRed(h.right) && !isRed(h.right.left)) {
// 右子树为2-结点,从左子树结点借
t = moveRedRight(h);
if (pp != null) {
adjustParentLink(h, pp, t);
}
h = t;
}
if (key.compareTo(h.key) == 0) {
// 命中非叶子结点,与后继结点交换
Node m = min(h.right);
swap(h, m);
// 删除替换后的后继结点
h.right = deleteMin(h.right);
break;
}
else {
// 继续遍历右子树
stack.push(h);
h = h.right;
}
}
}
// 调整删除结点后的二叉树,以满足红黑树的性质
Node b;
while (!stack.isEmpty()) {
h = stack.pop();
h.n--;
b = balance(h);
if (!stack.isEmpty()) {
t = stack.peek();
adjustParentLink(h, t, b);
} else {
return b;
}
}
return null;
}
6 有序性相关方法
6.1 floor(),ceiling()
- floor() :查找小于等于给定key的最大键
执行流程如下:
- 遍历树,从根结点开始
- 比较key与当前结点key大小cmp
- 如果key等于当前节点key直接返回
- 如果key小于当前结点key,表明要么有,要么在左子树中,继续遍历左子树
- 如果key大于当前结点key,表明当前结点为目前为止小于等于key的最大结点;记录当前结点,继续遍历右子树。
- 循环结束,返回结果
非递归实现如下:
/**
* 查找小于等于给定key的最大键
* @param key 指定key
* @return 小于等于给定key的最大键
*/
public K floor(K key) {
if (key == null) {
throw new IllegalArgumentException("argument to floor() is null");
}
if (isEmpty()) {
throw new NoSuchElementException("calls floor() with empty symbol table");
}
Node x = floor(root, key);
if (x == null) {
throw new NoSuchElementException("argument to floor() is too small");
} else {
return x.key;
}
}
/**
* 查找以x为根结点树中小于等于给定key的最大键
* @param key 指定key
* @return 小于等于给定key的最大键
*/
private Node floor(Node x, K key) {
Node t = null;
while (x != null) {
int cmp = key.compareTo(x.key);
if (cmp == 0) {
// 名字直接返回
return x;
} else if (cmp < 0) {
// 给定键小于当前结点键,继续遍历左子结点
x = x.left;
} else {
// 目前为止当前结点为小于等于key的最大结点
t = x;
x = x.right;
}
}
// 返回最终小于等于给定key的最大键
return t;
}
注:ceiling()方法同理,代码参考仓库
6.2 rank()
- rank(K key):查找小于key的键的数量
- rank(K key,Node x):查找以x为根结点树小于key的键的数量
rank(K key,Node x)算法思想:
- 如果x为空,返回0
- 比较key与当前结点key的大小,结果cmp
- 如果cmp小于0,查找左子树中小于key的数量
- 如果cmp大于0,计数为:1(当前结点) + 左子树中键的数量+查找右子树中小于key的数量
- 如果相等,计数初始化为左子树中键的数量
非递归实现如下:
/**
* 查找小于key的键的数量
* @param key 给定的key
* @return 小于key的键的数量
*/
public int rank(K key) {
if (key == null) {
throw new IllegalArgumentException("argument to rank() is null");
}
return rank(key, root);
}
/**
* 查找以x为根结点小于key的键的数量
* 算法:
* 当前结点为空,返回0
* 比较key与当前结点key大小
* 如果key小于当前结点的key,返回:左子树中的小于key的键的数量
* 如果key大于当前结点的key,返回:1+当前结点左子树键数量+右子树中小于key的数量
* 1 为当前结点
* 如果key等于当前节点中的key,返回:当前结点左子树键的数量
*
* @param key 给定的key
* @return 小于key的键的数量
*/
private int rank(K key, Node x) {
// 记录经过的结点
Stack<Node> nodes = new Stack<>();
// 同步记录下一个结点是左子结点还是右子结点,0表示左,1表示右
Stack<Integer> dir = new Stack<>();
// 计数
int c = 0;
while (x != null) {
int cmp = key.compareTo(x.key);
if (cmp < 0) {
// 小于当前结点,记录结点,继续查找左子树
nodes.push(x);
dir.push(0);
x = x.left;
} else if (cmp > 0) {
// 大于当前结点,记录结点,继续查找右子树
nodes.push(x);
dir.push(1);
x = x.right;
} else {
// 命中当前结点,计数初始化为左子树结点个数
c = size(x.left);
break;
}
}
while (!nodes.isEmpty()) {
x = nodes.pop();
if (dir.pop() == 1) {
c += 1 + size(x.left);
}
}
return c;
}
6.3 keys()
- keys(K lo, K hi):位于[lo,hi]之间键的集合
- 算法思想
- 寻找树中位于该范围内左侧临界点
- 按中序遍历判断当前键是否在[lo,hi]范围内,在加入队列;
- 判断当前结点键是否小于最大值hi
- 是,继续遍历后继节点
- 不是,超出范围,结束
源代码如下:
/**
* 位于[lo,hi]之间键的集合
*
* @param lo 低位key
* @param hi 高位key
* @return [lo, hi]之间键的集合
*/
public Iterable<K> keys(K lo, K hi) {
if (lo == null) {
throw new IllegalArgumentException("first argument to keys() is null");
}
if (hi == null) {
throw new IllegalArgumentException("second argument to keys() is null");
}
Queue<K> queue = new LinkQueue<>();
// if (isEmpty() || lo.compareTo(hi) > 0) return queue;
keys(root, queue, lo, hi);
return queue;
}
/**
* 以x为根结点树中位于[lo,hi]之间键的集合
*
* @param lo 低位key
* @param hi 高位key
* @return [lo, hi]之间键的集合
*/
private void keys(Node x, Queue<K> queue, K lo, K hi) {
Stack<Node> s = new Stack<>();
while (x != null || !s.isEmpty()) {
while (x != null && lo.compareTo(x.key) < 0) {
// 当前结点键大于低位键lo,继续遍历左子树
s.push(x);
x = x.left;
}
if (!s.isEmpty()) {
if (x == null) {
x = s.pop();
}
// lo <= x.key <= hi ,加入队列
if (lo.compareTo(x.key) <= 0 && hi.compareTo(x.key) >= 0) {
queue.offer(x.key);
}
}
if (x != null && hi.compareTo(x.key) > 0) {
// 当前结点key小于最大值hi,继续遍历右子树
x = x.right;
} else {
// 当前结点key大于等于最大值hi,结束
break;
}
}
}
到此处,关于算法第四版红黑树主要方法,讲解完毕。下面分析下性能,之后和标准红黑树做下对比。
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10