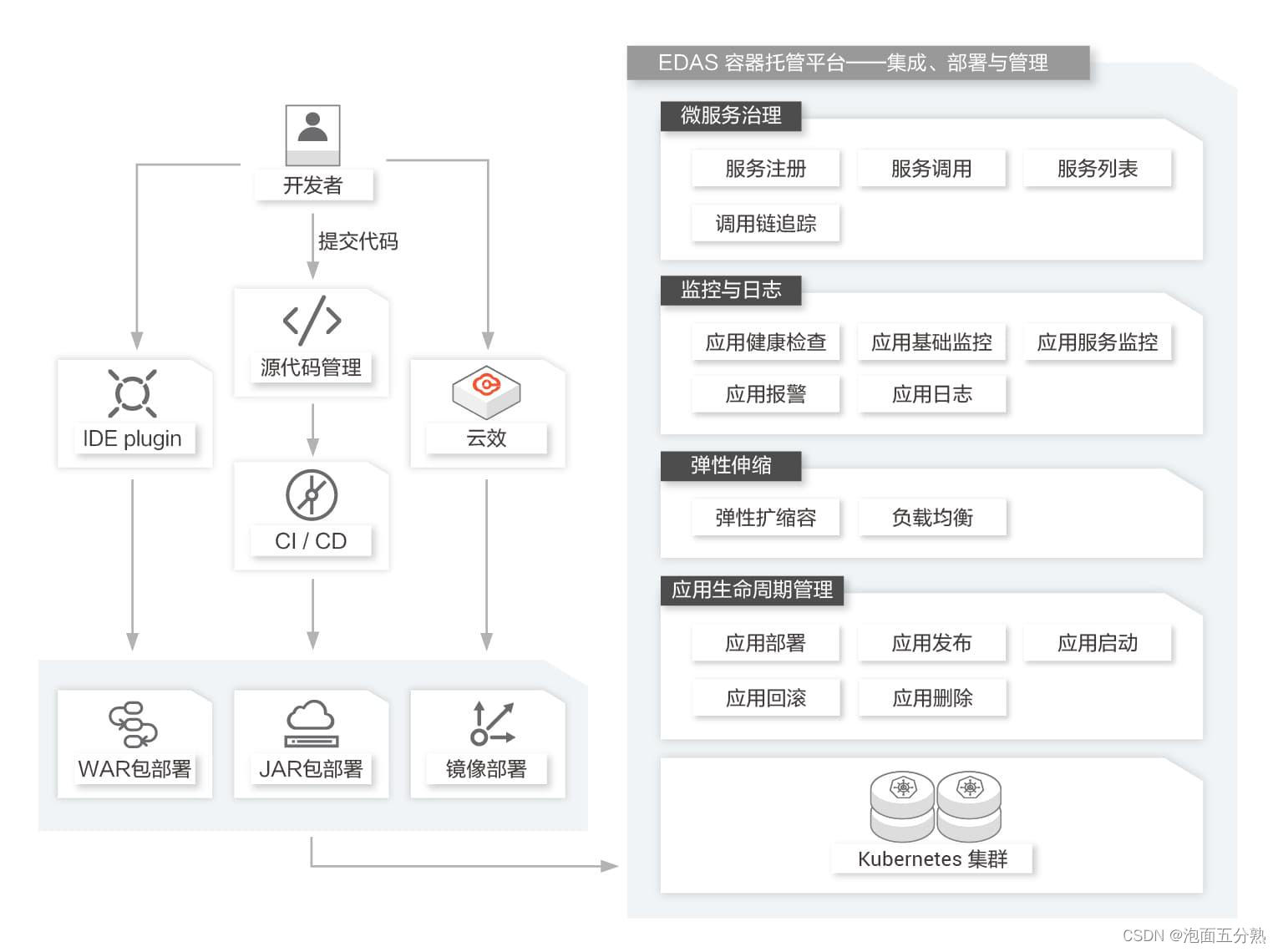
SmoothNLP新词发现算法的改进实现

背景介绍

新词发现也叫未登录词提取，依据 《统计自然语言处理》(宗成庆)，中文分词有98%的错误来自"未登录词"。即便早就火遍大江南北的Bert也不能解决"未登录词"的Encoding问题，便索性使用‘字’作为最小单元。

未登录词除了来自各行各业的专有名词、缩略语外，还有与时俱进的流行词、新生词，所以通过有监督大量标注的方式性价比过低。

一个行业的词库构建往往都是从0开始的，迁移使用也就是治标不治本。而且没有几个专业人员敢保证坐在那里就能滔滔不绝的把行业内所有词汇撰写下来，所以新词发现也是构建词库的重要辅助工具。

另外最近遇到的热词提取的需求越来越多，热词首先要定位好词，对于新出现的词，即便大量出现也会由于分词器不能正确识别的缘故难以上榜。

和其他AI算法一样，新词发现也有基于BiLSTM+CRF进行序列化标注的有监督算法，也有不需要标注的无监督算法。我个人看来，与其倾注时间在有监督的预训练标注，不如多花花心思在无监督结果确认上。无监督的新词发现，不管是轻量易用的Jieba、丰富工业API的HanLP、还是高校自研的LTP、Thulac、Pkuseg都有实现无监督的新词发现（有的叫关键短语提取）。这些新词发现基本都是基于TFIDF、自由度、凝聚度（部分引入HMM），接下来我就介绍一下业界常用到的NLP工具SmoothNLP中的新词发现——基于自由度和凝聚度的新词发现。

基于自由度和凝聚度的新词发现

一些简单的名词

• 词元（gram）: 定义语料中文字存在最小单位，可以是字可以是分词结果的词。由N个词元组成的新词元叫N词元（NGram），比如规定每个字都是一个词元，则‘华宇信息’就是一个4词元。以下对词元均简称G。
• 自由度 : 何为自由度，指的就是如果一个或几个词元组合可以成新词nG，它应当出现在丰富的语境中，换句话说就是这个新词比较自由，没有什么特定的和其他词元Gi一起出现的规则，因为如果有，就说明有可能nG应该和Gi组成新词(n+1)G
• 凝聚度 : 何为凝聚度，就是指组成新词nG的各个词元(G1,…,Gi)应该展现出一定的关联性，或者规律性。

SmoothNLP的定义

• 以每个字作为词元，这样的好处是避免了分词器的干扰，比如语句‘随着芈月传播出 ’分词结果是['随着 ','芈月 ','传播 ','出 ']，如果基于这个生成新词，那么永远不可出现‘芈月传 ’，所以用字作为词元
• 在SmoothNLP中将自由度用左右临近信息熵(Left and Right Entropy,LRE)来表示。
• 在SmoothNLP中将凝聚度用平均互信息(Average Mutual Information,AMI)来表示。

左右临近信息熵

信息熵

信息熵是对信息量多少的度量，信息熵越高，表示信息量越丰富、不确定性越大。相反越小则纯度越高。对于集合D有N个样本di，定义每个样本概率为Pdi，则集合D的信息熵为：
$${\mathbf{Entropy}}_D=-\sum _{(d_i\in D)}P(d_i){\log }_{2}P(d_i)$$

临近词元信息熵

SmoothNLP将候选词nG的临近字（SmoothNLP定义的词元是字）两两组合构成集合，并定义每个样本概率为nG与临近字Gi的条件概率，计算该集合的信息熵。由左临近字构成的集合信息熵就是左临近信息熵，由右临近字构成的集合信息熵就是右临近信息熵，具体公式为
$${\mathbf{LE}}_{nG}=-\sum _{(G_i\in G_{left-neighbor})}P(G_i|nG){\log }_{2}P(G_i|nG)$$
$${\mathbf{LE}}_{nG}=-\sum _{(G_j\in G_{right-neighbor})}P(G_j|nG){\log }_{2}P(G_j|nG)$$

综合左右临近信息熵

左右单侧的信息熵高并不能说明问题，要将左右信息熵综合考虑，这里SmoothNLP的做法是对左右临近信息熵取对数平均值：
$$\mathbf{LRE}=\log \frac{LE\ast e^{RE}+RE\ast e^{LE}}{|LE-RE|}$$

Tire

为了实现上述逻辑，方便查询N词元的左右临近字，选取字典树Tire存储。

举个栗子

以市场监督管理局数据2W条留言标题为测试样例为例。

很明显‘混凝’只有跟‘土’，‘凝土’前面只有‘混’，而‘混凝土’前后的就多了去了，所以‘混凝土’大概率是个词。

平均互信息

互信息

互信息是衡量随机变量之间相互依赖程度的度量，假如看见一个背电脑包戴帽子的小伙子，那么‘他职业是程序猿 ’是个随机事件，‘他帽子下是秃头 ’同样是个随机事件，那么这两个随机事件互相依赖的程度是‘已知他职业是程序猿的情况下，他帽子下是秃头的可能性 ’与‘已知帽子下是秃头的情况下，他职业是程序猿的可能性 ’之差，具体公式是：
$$\mathbf{MI}=\sum _{y\in Y}\sum _{x\in X}P(x,y)\log \frac{P(x,y)}{P(x)P(y)}$$

N词元互信息

SmoothNLP并没有严格按照互信息公式，而是使用点间互信息(point-wise mutual information，PMI)，假设新词nG由N个词元Gi构成，则该新词PMI为
$$\mathbf{PMI}={\log }_2\frac{P(G_1,...,G_i)}{{\prod }_{G_i\in nG}P(G_i)}$$

N词元平均互信息

由于点间互信息的值会受到候选词长度的影响——候选词越长，互信息取值偏大，所以使用平均互信息:
$$\mathbf{AMI}=\frac{1}{n}\mathbf{PMI}$$

在SmoothNLP的实现上做优化

SmoothNLP调皮了

不知什么原因，SmoothNLP很调皮并没有按照上述公式一板一眼的实现，而是加入一些论文中没有提到的‘个人想法’。

# 语料分批读取chunk_size
for corpus_batch in corpus:
	# 删除非中文、非英文、非数字字符
	del_unused_char()
	# 遍历处理后语料
	for line in corpus_batch :
		# 遍历1词元以及min到max+1词元
		for n in [1]+[min,max+1]:
			# 构建N词元词频字典
			n_gram_freq_dict[n] = build_n_gram_freq_dict()
			# 删除频率低于min_freq的N词元
			del_low_freq_n_gram()

for n in [min,max]:
	# 利用N+1词元词频字典构建N词元左右Tire
	left_tire,right_tire = build_tire_from_up(n_gram_freq_dict[n+1])
	# 计算N词元左右信息熵
	gram_n_lre_dict[n] = cal_lre(left_tire,right_tire)

# 计算1词元频率总和
gram_1_total = cal_gram_1_total(n_gram_freq_dict[1])

for n in [min,max]:
	# 计算N词元总和
	gram_n_total = cal_gram_n_total(n_gram_freq_dict[n])
	# 计算N词元平均互信息
	gram_n_pmi_dict[n] = cal_pmi(n_gram_freq_dict[1],gram_1_total,n_gram_freq_dict[n],gram_n_total)
	# 计算N词元评分
	gram_n_score_dict[n] = cal_score(gram_n_pmi_dict[n],gram_n_lre_dict[n])

# 统计所有词元首词元,统计所有词元尾词元
start_gram_freq,end_gram_freq = build_start_end_gram_freq(gram_n_score_dict)

# 移除包含频率高于阈值 首尾词元的词元
result = drop_some_gram(gram_n_score_dict,start_gram_freq,end_gram_freq)

# 排序
result.sort()	

单从算法逻辑上可以发现以下几个问题：

• 语料是分批读取的，而且删除频率低于min_freq的N词元是在一个批内执行的，这样会误删一些‘单批内词频低，但总体词频高于min_freq’的候选词
• 他是根据N+1词元频率构建的N词元左右Tire，这样考虑是因为他是以字为词元的，那么N+1词元就可以拆分成‘首字词元+N词元’或‘N词元+尾字词元’。但其实大可不必浪费时间额外统计一次max+1词元频率。
• 另外好多统计操作其实是可以在一个预语料循环里完成的。
• 还有好多中间变量是应该回收的

总体优化

针对以上问题我做了以下调整【Smoothnlp为左图，我实现的右图】

删除频率低于min_freq的N词元我拿到了计算评分时做。

可以发现在我的算法没有提及[min,max]的遍历，是因为我写的只是一个n词元，没错我也调皮了，不过我调皮一下使算法多线程成为可能。

这里我们再看一下SmoothNLP在多线程方面的尝试：

看来这个todo要我们来写了，其实他不写也是有原因的，对比看一下简化的逻辑图便知，先看SmoothNLP。

每元计算都是在词频上关联的，多线程就要一个等一个

再看看我们的

移除不必要的max+1词元计算，我们在第一次遍历语料时就顺带创建左右临近树的元素列表了。省了一次计算并使得每元计算解耦，这样就使得多线程成为可能。

细节优化

再具体公式实现上，Smoothnlp也并没有严格实现以及一些牺牲一部分精度：

• 公式中常量值或对数底数采取了取近似值
• 定义高频首末词元的阈值很小，比例在小数据集上效果不会太好
• 保留数字和英文，这方面的新词还是比较少的，但出现的自由度越普遍很高。
• 由于分批读取的缘故在频率字典融合时使用Update反而会覆盖原本有的，而不是与原本的相加。

既然我们能多线程了，就不近似了也不牺牲精度了，也解决巴拉巴拉的问题。

另外这里详细说一下我们是怎么实现‘第一次遍历语料时就顺带创建左右临近树的元素列表’的。

Smoothnlp遍历语料生成词元其实就是返回N长的字符串子串，而我们定义了一种数据结构，一种元组。

Tuple[Tuple[],Tuple[],Tuple[]]

这元组里有三个元素：

• 第一个是左临近词元元组，只有一个元素，左临近词元
• 第二个是N词元元组，是组成N词元的每个词元
• 第一个是右临近词元元组，只有一个元素，右临近词元

之后使用Python的Counter就轻松实现Tire树的数据字典的构建。

这种实现又方便了基于分词结果的新词发现。

另外SmoothNLP是直接将‘无效字符’替换成掉，这样会带来一个问题，比如例句。

“根据《劳动法》规定能保护…”

我们希望看到的肯定是【‘根据’ ‘劳动法’ ‘规定’ ‘能’ ‘保护’】，但是由于直接替换掉，变成了 “根据劳动法规定能保护…”，那么在计算2次元结果就变成了【‘根据’ ‘劳动’ ‘法规’ ‘定能’ ‘保护’】，这是对提出‘劳动法’这个词的干扰。

优化效果

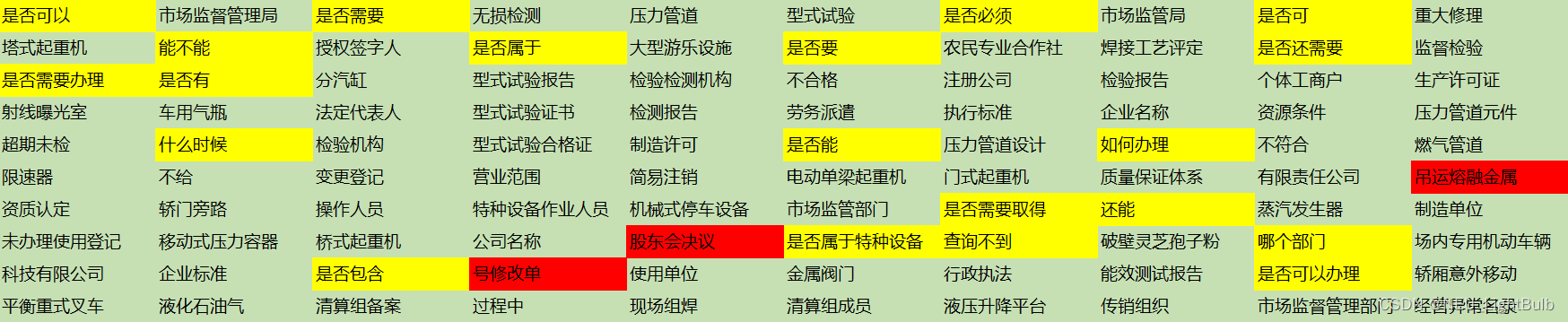
看下效果，都是基于【某政府机关网站2W条留言标题数据】的新词发现，最小2词元，最多5词元，最小词元频率5 。smoothnlp效果如下，绿色是正常有效词，黄色是正常无效词，红色是不正常的词：

我的优化效果如下：

基于分词结果的新词发现

虽然Smoothnlp依靠‘芈月传’的例子摒弃了，基于分词结果的新词发现，但是不可否认的是，基于字的新词发现往往都是分词词典里已经有了的短词，换句话说基于分词结果的新词发现并不是没有意义，相反他的效率也许更高。

所以我实现了基于字和基于分词两种新词发现，后者是使用jieba默认词典分词的。

基于【某政府机关网站2W条留言标题数据】，最小2词元，最多3词元，最小词元频率5效果如下：

一点点想法

我计划基于这个制作一个根据语料构建行业词典的辅助服务。

本文多是个人的一些理解欢迎交流、欢迎批评指正。