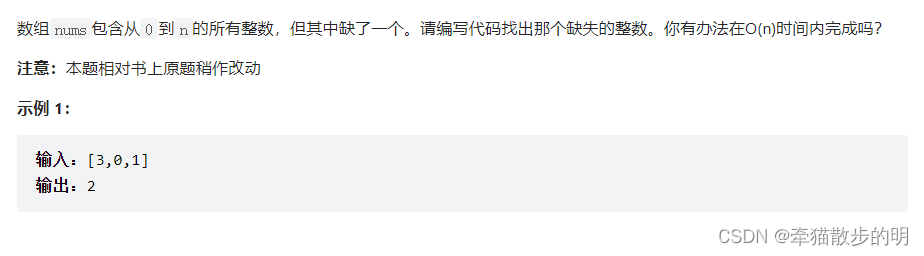
消失的数字

解法一：求和相减

假设nums为[0,1,2,4],消失的数字为3，完整的数组应该是[0,1,2,3,4]，则sum1=0+1+2+4=7,sum2=0+1+2+3+4=10，我们很容易发现
sum2-sum1 = 0+1+2+3+4 - 0+1+2+4 = 3，即为消失的数字。因此，我们可以采用先相加再相减的方法，就可以求出消失的数字。
代码如下：

int missingNumber(int* nums, int numsSize)
{
	int tmp = 0;
	int talg = 0;
	for (int i = 0;i <= numsSize;i++)
	{
		tmp = tmp + i;//求数组下标之和
	}
		for (int j = 0;j < numsSize;j++)
		{
			talg += nums[j];//求数组元素之和
		}
		return tmp - talg;
}

解法二：异或

首先我们得清楚异或 ^ 的原理：
相同为0，相异为1，并且0^任何数都等它本身
a ^ a = 0、a ^ b = b ^ a、0 ^ a = a 、(a!=b)
那么根据上述的原理我们便可以使用异或进行解题：
首先异或上所有数，n即为此数组元素个数，即ret = 0 ^ 1^ 2^ …^n
然后对数组元素异或，nums[0]^ nums[1] ^ …^ nums[numsSize-1]
然后异或这二者，即
ret = 0^ 1^ 2^ 3^ …^ n^ nums[0] ^ nums[1]^ …^nums[numsSize-1]
最终ret就为消失的数字
打个比方：nums[] = {2,3,4,5,6}
ret = 0 ^ 1 ^ 2 ^ 3 ^ 4 ^ 5 ^ 6 ^ 2 ^ 3 ^ 4 ^ 5 ^ 6 = 1.

int missingNumber(int* nums, int numsSize)
{
    //异或
    int ret = 0;
    //先异或0-n的所有数
    for(int i = 0; i <= numsSize; ++i){
       ret ^= i;
    }
    //再将ret与数组所有数异或
    for(int i = 0; i < numsSize; ++i){
       ret ^= nums[i];
    }
    return ret;
}

数组中出现的次数

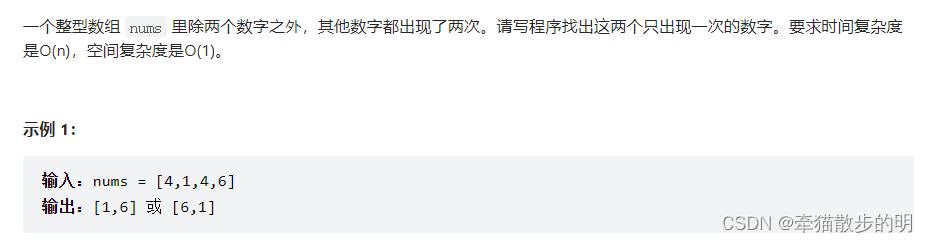
同上可得，此题采用异或的位运算是最合适的。

int* singleNumbers(int* nums, int numsSize, int* returnSize) {
    int ret = 0;
    int i = 0;
    int num1 = 0;
    int num2 = 0;
    int pos = 0;
    int* arr = (int*)malloc(2 * sizeof(int));
    //通过0对自身依次异或，将两个单独的数的异或后的结果找出
    for (i = 0; i < numsSize; i++)
    {
        ret ^= nums[i];
    }
    //找到异或后结果的二进制序列，找出为1的位数
    for (i = 0; i < 32; i++)
    {
        if ((ret >> i) & 1 == 1)
        {
            pos = i;
            break;
        }
    }
    //找到位数后，将按其他数的这个位数是否为1，还是为0进行分离，形成两组数，分别自身异或，最后剩下的就是单独的数。
    for (i = 0; i < numsSize; i++)
    {
        if ((nums[i] >> pos) & 1 == 1)
        {
            num1 ^= nums[i];
        }
        else
        {
            num2 ^= nums[i];
        }
    }
    arr[0] = num1;
    arr[1] = num2;
    *returnSize = 2;
    return arr;
}