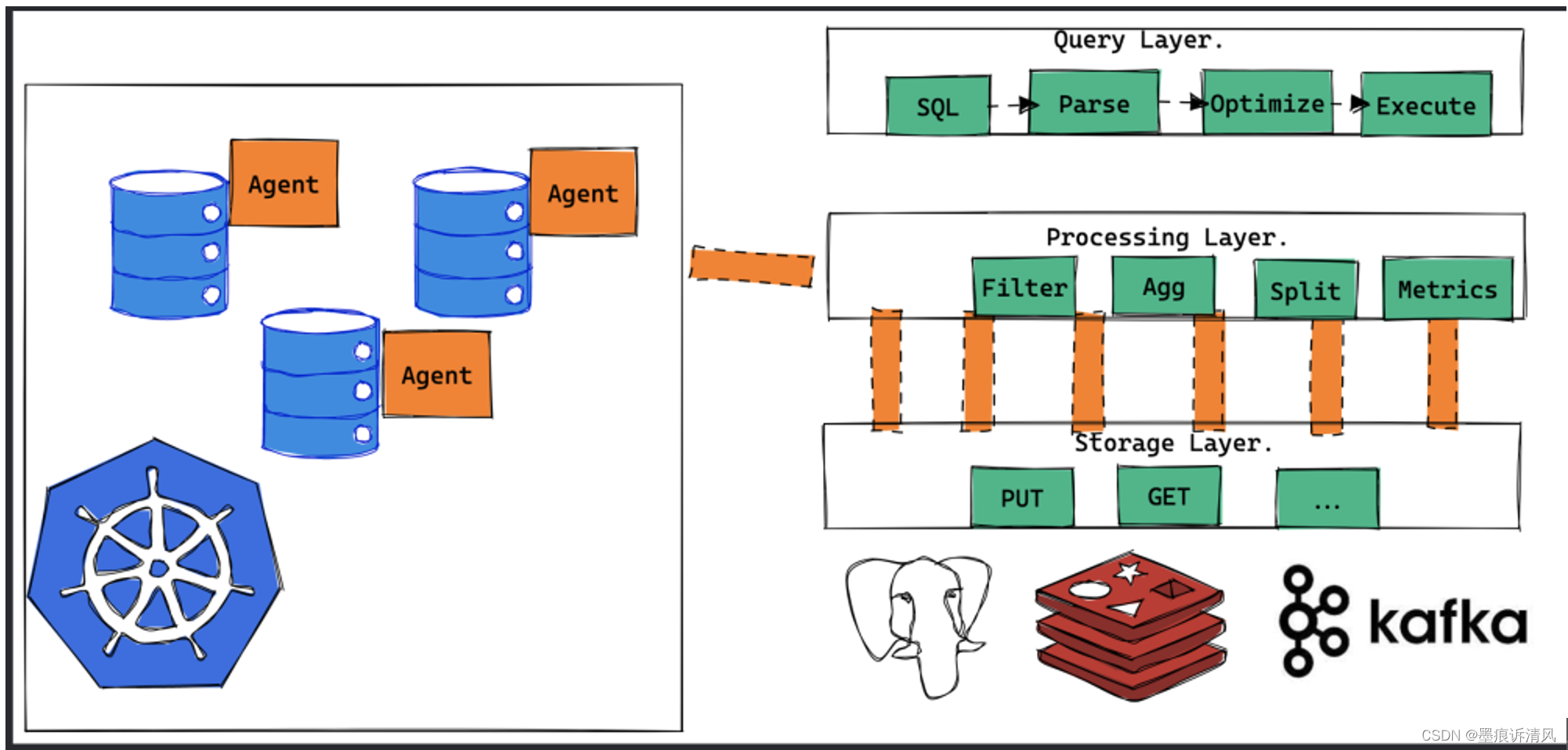
点睛
Prim与Kruskal算法是用来求图的最小生成树的算法。最小生成树有n个顶点,n-1条边,不能有回路。
Prim算法
Prim算法的特点是从个体到整体,随机选定一个顶点为起始点出发,然后找它的权值最小的边对应的另一个顶点,这两个顶点就构成了新的个体(连通图),然后在这两个顶点的所有边中找权值最小的边对应的另一个顶点(前提是加进来不能导致已有的顶点所在的连通图构成回路),就这样直到所有顶点都并入同一个连通图,算法结束。
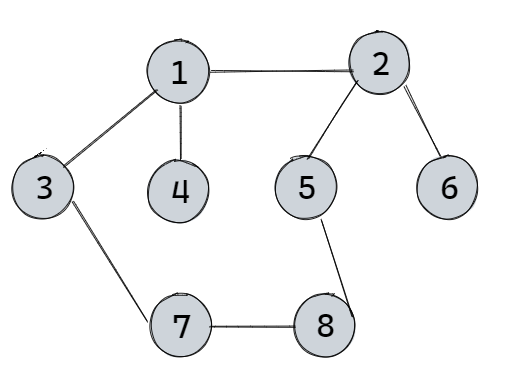
例1利用Prim算法求下图的一棵最小生成树,设顶点1为起始点,写出求解过程。

答案:
找到顶点1权值最小的边(1,3),则顶点1和3构成新的连通图
找到顶点1和3中权值最小的边(3,4),则顶点1,3,4构成新的连通图
找到顶点1,3,4中权值最小的边(4,7),则顶点1,3,4,7构成新的连通图
找到顶点1,3,4,7中权值最小的边(7,8),则顶点1,3,4,7,8构成新的连通图
找到顶点1,3,4,7,8中权值最小的边(8,6),则顶点1,3,4,7,8,6构成新的连通图
找到顶点1,3,4,7,8中权值最小的边(8,5),则顶点1,3,4,7,8,6,5构成新的连通图
找到顶点1,3,4,7,8,5中权值最小的边(1,2),则顶点1,3,4,7,8,6,5,2构成新的连通图
至此Prim算法结束,找到最小生成树如下图

Kruskal算法
Kruskal算法的特点是从整体到个体,它把整个图(默认是无向连通图)看做n个独立的顶点,然后把图的所有带权边根据权值大小升序排列存入一个序列中。最后依次从序列中取出这些边加入n个独立的顶点使它们成为同一个连通图的一部分,只要取出的边的数量不到n-1就一直取。在取的过程中如果有一条边的加入会造成回路,则跳过选下一个权值稍大的边。
例2利用Kruskal算法求下图的一棵最小生成树,写出求解过程。

答案:
将图中所有的边按照权值大小升序排列存入集合中,结果如下:
{(1,2), (1,3), (1,4), (2,5), (2,6), (3,4, (3,7), (4, 5), (4,7), (5,6), (5, 8), (6,8), (7,8)}
从集合中取出边(1,2),顶点1和2构成一个新的连通图
从集合中取出边(1,3),顶点1,2,3构成一个新的连通图
从集合中取出边(1,4),顶点1,2,3,4构成一个新的连通图
从集合中取出边(2,5),顶点1,2,3,4,5构成一个新的连通图
从集合中取出边(2,6),顶点1,2,3,4,5,6构成一个新的连通图
从集合中取出边(3,4),会在顶点1,3,4之间构成回路跳过
从集合中取出边(3,7),顶点1,2,3,4,5,6,7构成一个新的连通图
从集合中取出边(4,5),会在顶点1,2,4,5构成回路,跳过
从集合中取出边(4,7),顶点1,3,4,7构成回路,跳过
从集合中取出边(5,6),顶点2,5,6构成回路,跳过
从集合中取出边(5,8),顶点1,2,3,4,5,6,7,8构成一个新的连通图
边的个数达到n-1,结束,最小生成树如下图: