先序
在了解查找算法之前,需要熟悉几个概念,不然后面容易产生理解错误。
查找表:即被查找的对象,通常由几个关键字组成。
关键字:就是数据项、字段的意思。关键字有主次之分,其中主关键字取值是唯一的。
查找长度:给定的关键字在查找表中的比较次数。(查找就是拿要找的数在对应的字段中一个个比较)
静态、动态查找:静态查找只执行查找操作(判断有无和位置在哪),不改变数据;动态查找除了查找还会改变数据。
一、顺序查找(静态查找)
原理:极其简单,就是拿给定值和对应的关键字中的所有数按照指定顺序(从前到后等)一个个比较知道找到或比较完所有值。
考点:顺序查找包括不带监视哨和带监视哨两种类型
不带监视哨的顺序查找
def SeqSearch(self, key):
iPos = 0 # 数据元素在查找表中的位置,从第一个开始
while iPos < self.length and self.data[iPos] != key:
iPos += 1 # 只要没找到就往后加1
return (iPos if iPos < self.length else -1) # 找到了返回对应位置;没找到返回-1上述代码中我们需要判断iPos < self.length,即防止越界。为了提高效率,可以把查找表的第一个元素作为监视哨。
带监视哨的顺序查找
def SeqSearch(self, key):
self.data[0].key = key # 将第一个元素作为监视哨
iPos = self.length - 1 # 从最后一个数据开始比较
while self.data[iPos].key != key:
iPos -= 1 # 没找到往前加而不是减一,就不可能越界,也就不用判断。
return iPos if iPos > 0 else -1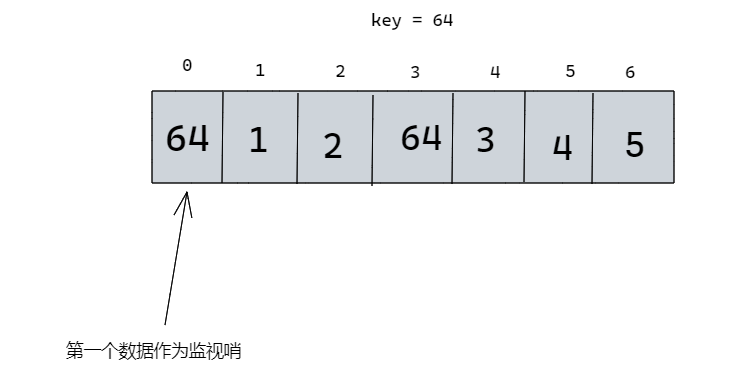
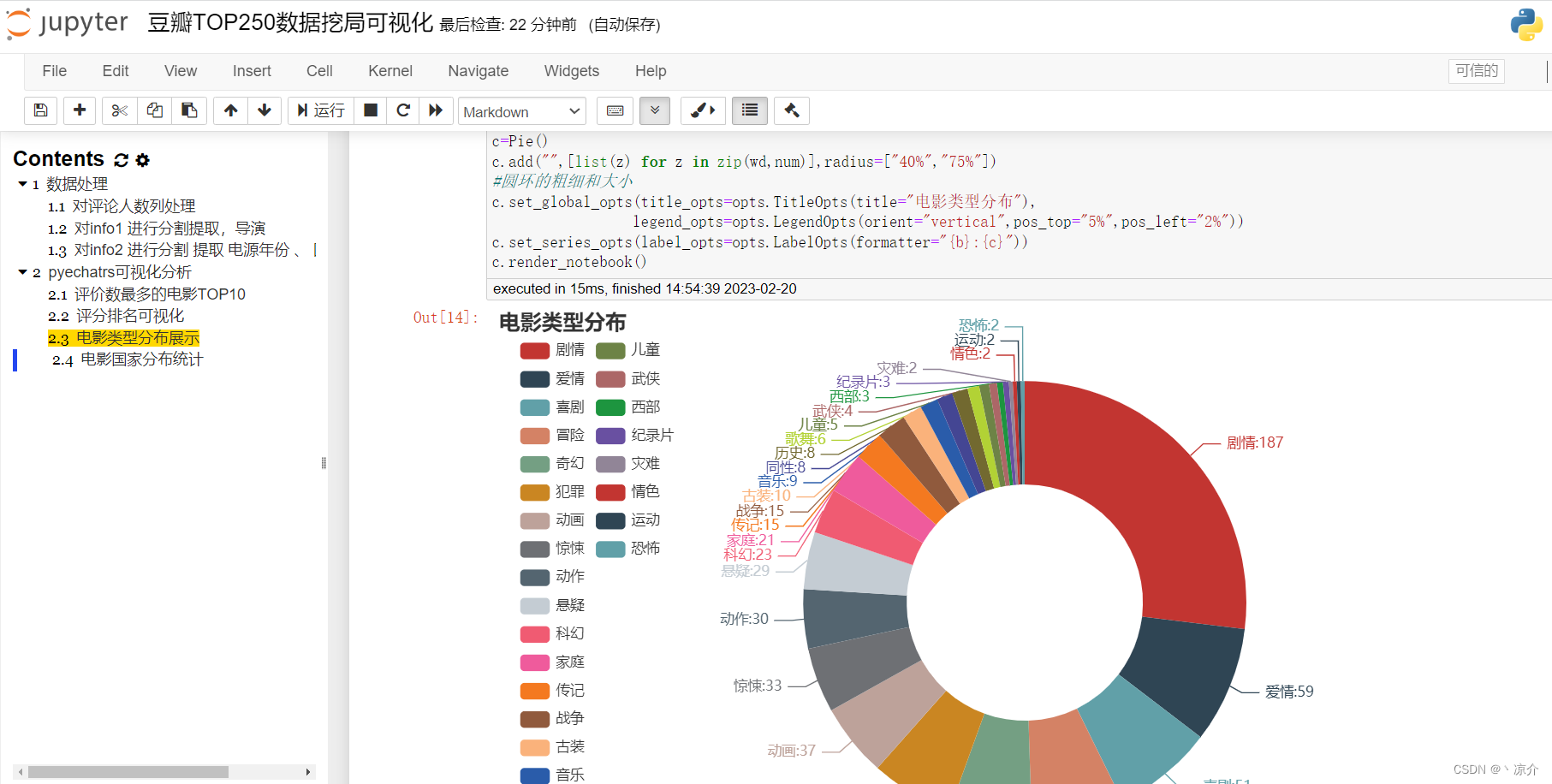
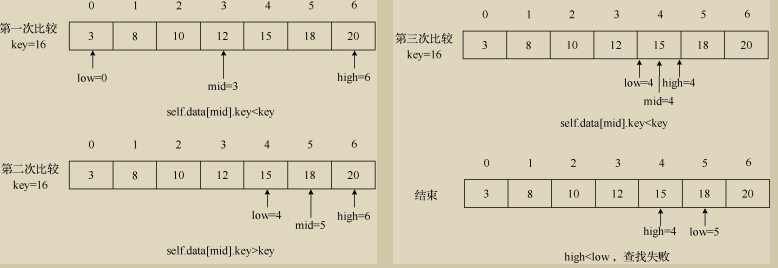
二、折半查找(静态查找)
条件:折半查找要求查找表必须是有序的
过程:
首先确定查找范围(左边low, 右边high,两者差大于等于0就有范围),若范围为空则查找失败
若范围不为空,则在查找范围的中间位置比较,若相同则查找成功
若小于中间数,则在中间数左边部分(low不变,high为中间位置减一)继续按照上述步骤查找(确定查找范围,比较中间数)
若大于中间数,则在中间数右边部分(high不变,low为中间位置加一)继续按照上述步骤查找(确定查找范围,比较中间数)
三、二叉排序树(动态查找)
二叉排序树的概念:
它要么是空树,要么是满足以下性质的二叉树:
① 若根结点的左子树非空,则左子树中所有结点的值都小于根结点的值。
② 若根结点的右子树非空,则右子树中所有结点的值都大于根结点的值。
③ 根结点的左、右子树均是一棵二叉排序树。
二叉排序树的创建:采用插入算法。很简单,根据给定的顺序,第一个被插入的作为根节点,后面插入的与根节点比较按照其性质放置在左右子树中。
例:关键字{11,12,8,5,10,15}

关键字{5,12,8,11,10,15}
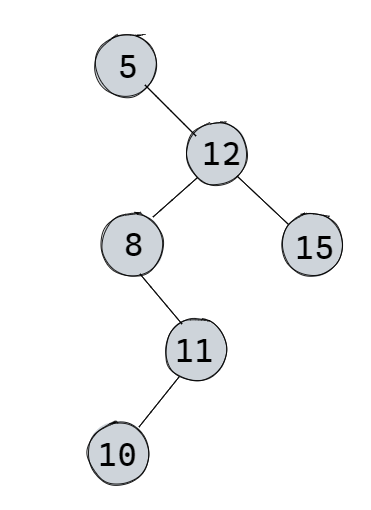
二叉排序树的查找:类似于折半查找,从根节点开始比较,然后往左右子树的根节点比较,就类似与折半查找比较中间位置。

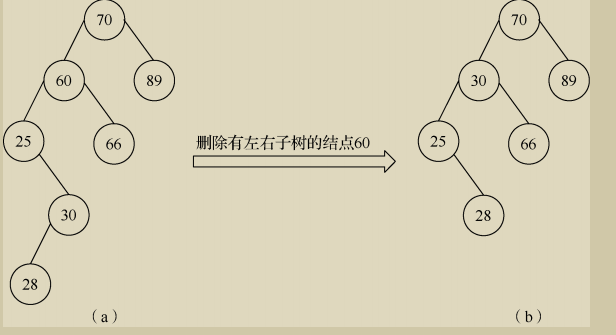
二叉树删除关键字:
分三种情况,被删除的节点为叶子结点、只有左子树或者右子树、左右子树都有。
前两种很简单,第一种直接删了,其双亲的指针域改成空;第二种让双亲指针指向下一个根节点即可
第三种提一下,有两种办法,下图的是其中一种,即找到要被删除的节点的左子树中最大的节点。然后把该删除的节点删掉用左子树的最大的节点补充即可。
当然还有第二种办法,就是找到右子树中最小的节点然后把该删除的删除,用右子树最小的节点代替即可。
四、平衡二叉树、B-树的概念(动态查找)
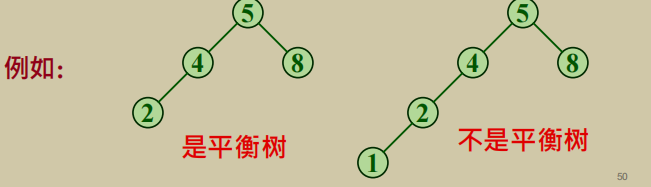
平衡二叉树:二叉树查找中二叉树的高度越小平均查找长度就会越小,所以平衡二叉树就是使得二叉树的深度尽可能的小并满足原来二叉树性质的特殊的二叉树。别名AVL树。
平衡二叉树的性质:每个节点的左右子树的深度之差的绝对值小于等于1(-1,0,1)
B-树:解决数据元素太大查找效率低下的问题。