相关课程： 音频信号处理及深度学习教程
傅里叶分析之掐死教程（完整版）更新于2014.06.06 - 知乎 (zhihu.com)

1.1.3 过零率

过零率：是一个信号符号变化的比率，即在每中语音信号从正变为负或从负变为正的次数。（语音识别、音乐信息检索，过零率越大，频率近似越高）

计算第t帧信号过零点数：

代码如下：

# 信号的过零率
# 0. 预设环境
import librosa
import numpy as np
from matplotlib import pyplot as plt
import librosa.display

# 1.加载信号
wave_path_absolute = r"E:\VoiceDev\audio_data\speech_this_song.wav"
wave_path = "../audio_data/music_piano.wav"
waveform, sample_rate = librosa.load(wave_path_absolute, sr=None)

# 2.定义函数，功能：计算每一帧的过零率
def Calc_ZCR(waveform, frame_length, hop_length):
    # 如果按照帧长来分割信号，余下部分不能形成一个帧则需要补0
    if len(waveform) % hop_length != 0:
        frame_num = int((len(waveform) - frame_length) / hop_length) + 1
        pad_num = frame_num * hop_length + frame_length - len(waveform)  # 补0个数
        waveform = np.pad(waveform, pad_width=(0, pad_num), mode="wrap")  # 补0操作

    frame_num = int((len(waveform) - frame_length) / hop_length) + 1
    waveform_zcr = []
    for t in range(frame_num):
        current_frame = waveform[t * (frame_length - hop_length):t * (frame_length - hop_length) + frame_length]
        a = np.sign(current_frame[0:frame_length-1, ])
        b = np.sign(current_frame[1:frame_length, ])
        current_zcr = np.sum(np.abs(a-b))/2/frame_length
        waveform_zcr.append(current_zcr)
    return np.array(waveform_zcr)

# 3. 设置参数：每一帧长1024，以50%的重叠率分帧，调用该函数
frame_size = 1024
hop_size = int(frame_size * 0.5)
waveform_ZCR = Calc_ZCR(waveform=waveform, frame_length=frame_size, hop_length=hop_size)

# 4.绘制图像
frame_scale = np.arange(0,len(waveform_ZCR),step=1)
time_scale = librosa.frames_to_time(frame_scale,hop_length=hop_size)
plt.figure(figsize=(20, 10))
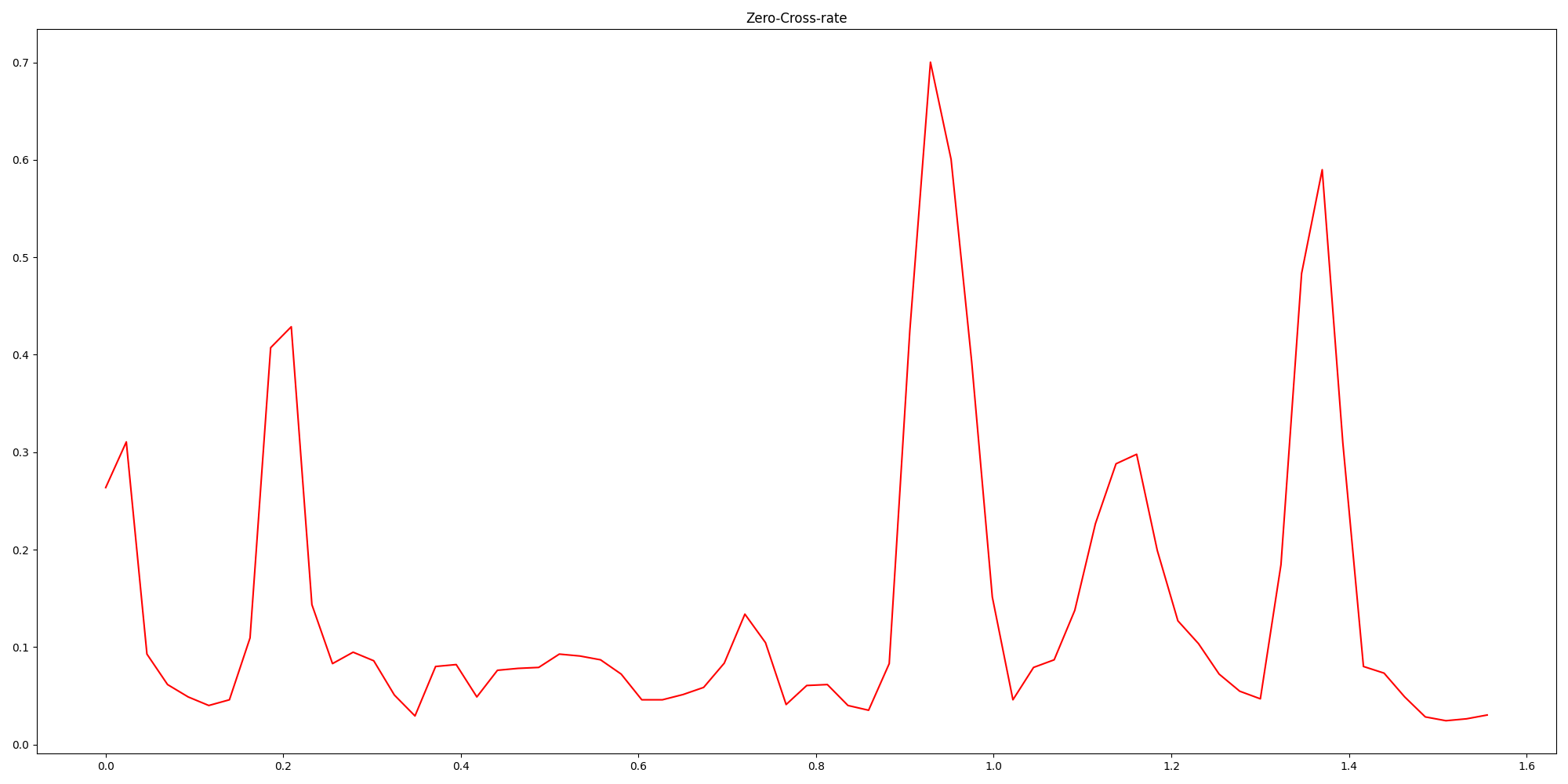
plt.plot(time_scale, waveform_ZCR, color='red')
plt.title("Zero-Cross-rate")
plt.show()

# 5. 利用librosa.feature
waveform_ZCR_librosa = librosa.feature.zero_crossing_rate(y=waveform, frame_length=frame_size, hop_length=hop_size).T[1:,0]
plt.figure(figsize=(20, 10))
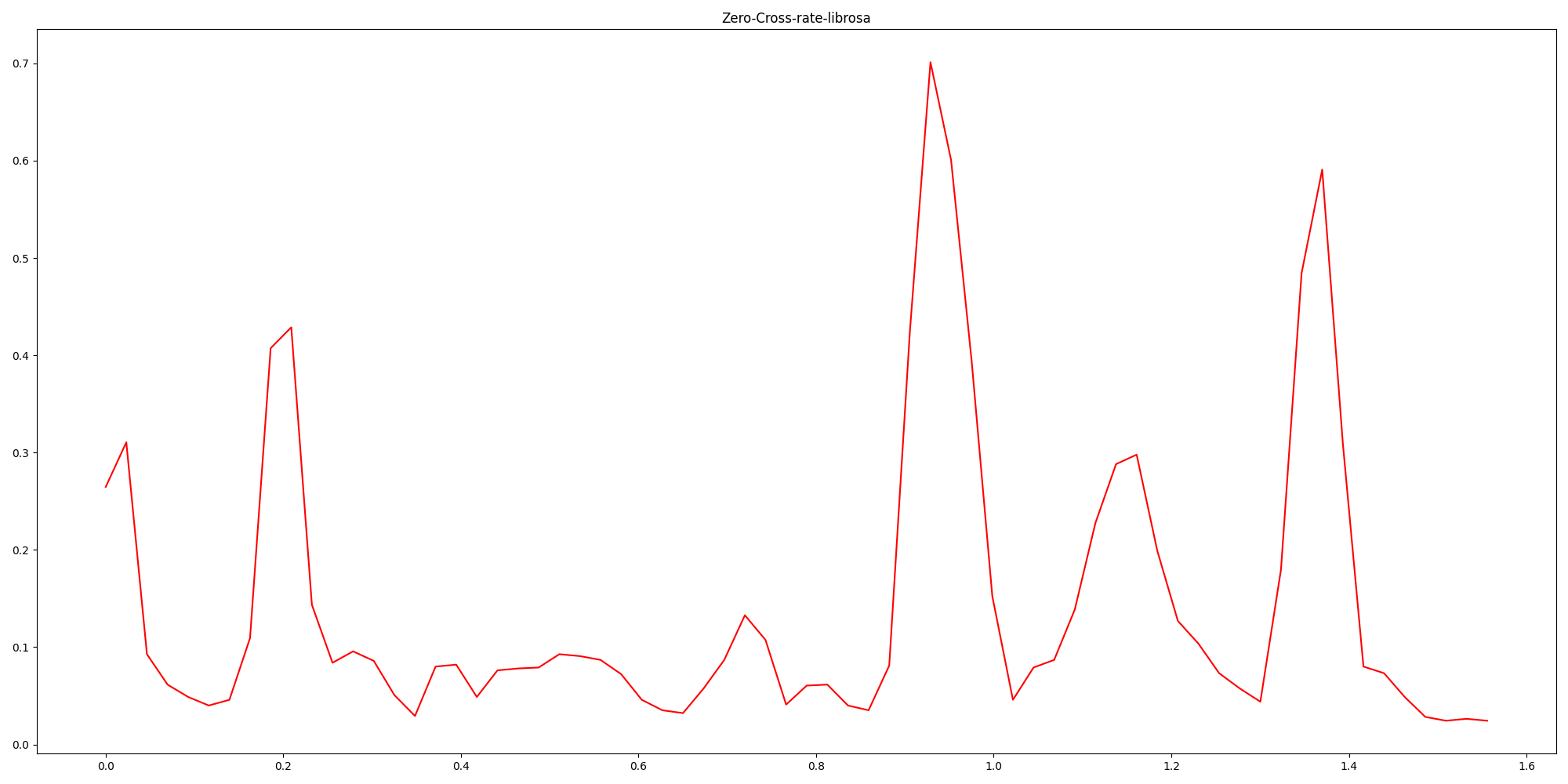
plt.plot(time_scale, waveform_ZCR_librosa, color='red')
plt.title("Zero-Cross-rate-librosa")
plt.show()

bias = waveform_ZCR_librosa - waveform_ZCR
print(f"the bias is {bias}\n Congratulation!")

运行结果：

使用自己写的函数结果图：

使用librosa库函数：

1.1.4 谱质心和子带带宽

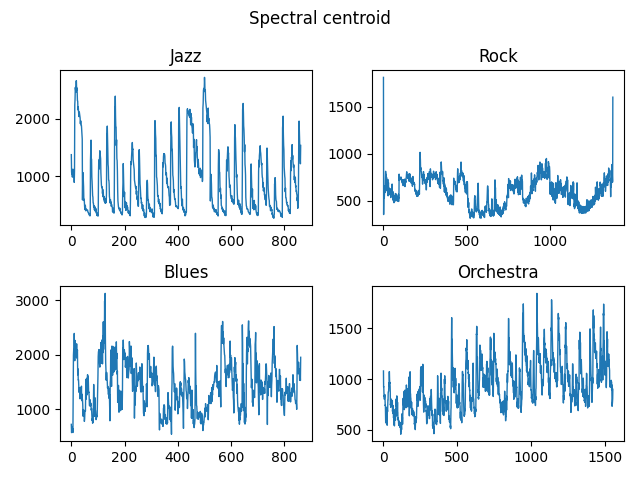
谱质心 Spectral centroid

频率成分的重心，是频谱中在一定频率范围内通过能量加权平均的频率，其单位是Hz。（声音的明亮度，低沉的声音谱质心低，欢快明亮的声音谱质心高，声色）

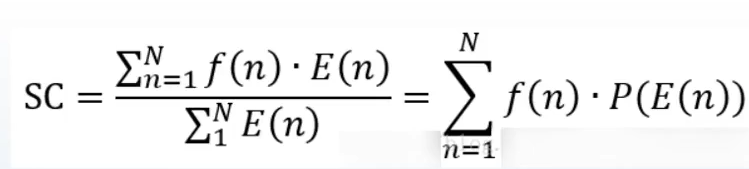
子带带宽 Bandwidth

在Spectral centroid的频谱范围，计算每一点到谱质心的距离的加权平均值（音频识别）

代码如下：

# 信号的频域特征
import librosa
import numpy as np
from matplotlib import pyplot as plt

# 1. 加载信号
jazz_path = r"E:\VoiceDev\audio_data\jazz.wav"
jazz, sr = librosa.load(jazz_path, sr=None)

rock_path = r"E:\VoiceDev\audio_data\rock.wav"
rock, sr = librosa.load(rock_path, sr=None)

blues_path = r"E:\VoiceDev\audio_data\blues.wav"
blues, sr = librosa.load(blues_path, sr=None)

orchestra_path = r"E:\VoiceDev\audio_data\orchestra.wav"
orchestra, sr = librosa.load(orchestra_path, sr=None)

# 2. 获取信号的Spectral centroid（谱质心）
sc_jazz = librosa.feature.spectral_centroid(y=jazz, n_fft=1024).T[:, 0]
sc_rock = librosa.feature.spectral_centroid(y=rock, n_fft=1024).T[:, 0]
sc_blues = librosa.feature.spectral_centroid(y=blues, n_fft=1024).T[:, 0]
sc_orchestra = librosa.feature.spectral_centroid(y=orchestra, n_fft=1024).T[:, 0]

fig, aix = plt.subplots(2, 2)
aix[0, 0].plot(np.arange(0, len(sc_jazz)), sc_jazz, linewidth=1)
aix[0, 0].set_title("Jazz")
aix[0, 1].plot(np.arange(0, len(sc_rock)), sc_rock, linewidth=1)
aix[0, 1].set_title("Rock")
aix[1, 0].plot(np.arange(0, len(sc_blues)), sc_blues, linewidth=1)
aix[1, 0].set_title("Blues")
aix[1, 1].plot(np.arange(0, len(sc_orchestra)), sc_orchestra, linewidth=1)
aix[1, 1].set_title("Orchestra")
fig.suptitle("Spectral centroid")
plt.show()

# 3. 获取信号的Spectral bandwidth
sw_jazz = librosa.feature.spectral_bandwidth(y=jazz, n_fft=1024).T[:, 0]
sw_blues = librosa.feature.spectral_bandwidth(y=blues, n_fft=1024).T[:, 0]
sw_rock = librosa.feature.spectral_bandwidth(y=rock, n_fft=1024).T[:, 0]
sw_orchestra = librosa.feature.spectral_bandwidth(y=orchestra, n_fft=1024).T[:, 0]

figure, aix = plt.subplots(2, 2)
aix[0, 0].plot(np.arange(0, len(sw_jazz)), sw_jazz, linewidth=1)
aix[0, 0].set_title("Jazz")
aix[0, 1].plot(np.arange(0, len(sw_rock)), sw_rock, linewidth=1)
aix[0, 1].set_title("Rock")
aix[1, 0].plot(np.arange(0, len(sw_blues)), sw_blues, linewidth=1)
aix[1, 0].set_title("Blues")
aix[1, 1].plot(np.arange(0, len(sw_orchestra)), sw_orchestra, linewidth=1)
aix[1, 1].set_title("Orchestra")
figure.suptitle("Spectral bandwidth")
plt.show()

运行结果：

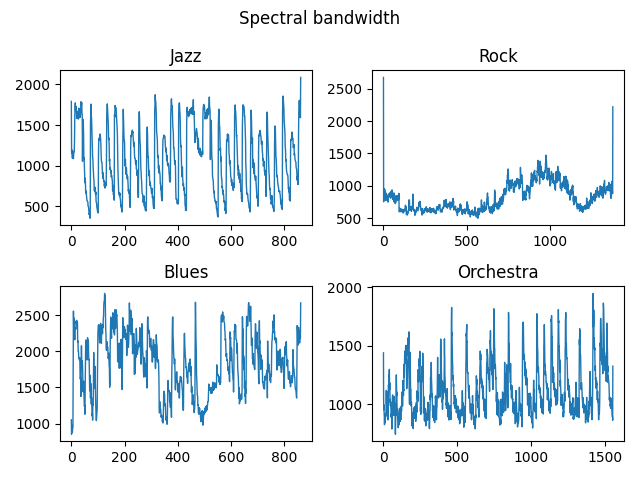
加窗处理：

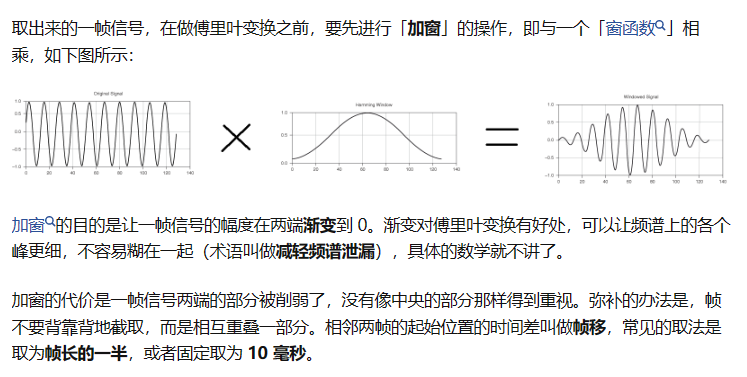
1.1.5 短时傅里叶分析法

由于声信号往往是随时间变化的，在短时间内可以近似看做平稳(对于语音来说是几十毫秒的量级)所以我们希望把长的声音切短，来观察其随时间的变化情况，由此产生STFT分析方式。

FFT与STFT对比
STFT在时域中对信号进行加窗处理 (分)，所以最终结果是有关时域频域的信息，时域的信息是每一帧帧长 (窗函数的长度)

关系:如果窗函数带宽长，则包络中的精细结构较少，疏松，得到窄带语谱图，有较好的频域分辨率，但时域分辨率较差，如果窗函数带宽窄，则包络中的精细结构较多，密集，得到宽带语谱图，有较好的时域分辨率，但频域分辨率较差;

获取不同时刻、不同频率的频谱图（能量分布情况）

代码如下：

import librosa
import numpy as np
from matplotlib import pyplot as plt

# 1.加载信号
wave_path = r"E:\VoiceDev\audio_data\music_piano.wav"
waveform, sample_rate = librosa.load(wave_path, sr=None)

# 2.信号分帧：补零->分帧->加窗
frame_size, hop_size = 1024, 512
if len(waveform) % hop_size != 0:
    frame_num = int((len(waveform) - frame_size) / hop_size) + 1
    pad_num = frame_num * hop_size + frame_size - len(waveform)
    waveform = np.pad(waveform, pad_width=(0, pad_num), mode="wrap")
frame_num = int((len(waveform) - frame_size) / hop_size) + 1
# 分帧 ?
row = np.tile(np.arange(0, frame_size), (frame_num, 1))
column = np.tile(np.arange(0, frame_num * (frame_size - hop_size), (frame_size - hop_size)), (frame_size, 1)).T
index = row + column
waveform_frame = waveform[index]
# 加窗 ?
waveform_frame = waveform_frame * np.hanning(frame_size)

# 3.信号做傅里叶变换np.fft.rfft(waveform_frame,n _fft)
n_fft = 1024
waveform_stft = np.fft.rfft(waveform_frame, n_fft)

# 4.功率谱函数
waveform_pow = np.abs(waveform_stft)**2/n_fft
waveform_db = 20 * np.log10(waveform_pow) # 分贝

# 5.绘制波形
plt.figure(figsize=(10,10))
plt.imshow(waveform_db)
y_ticks = np.arange(0,int(n_fft/2),100)
plt.yticks(ticks=y_ticks,labels=y_ticks*sample_rate/n_fft)
plt.title("Waveform_STFT")
plt.show()

运行结果如下：

得到语谱图

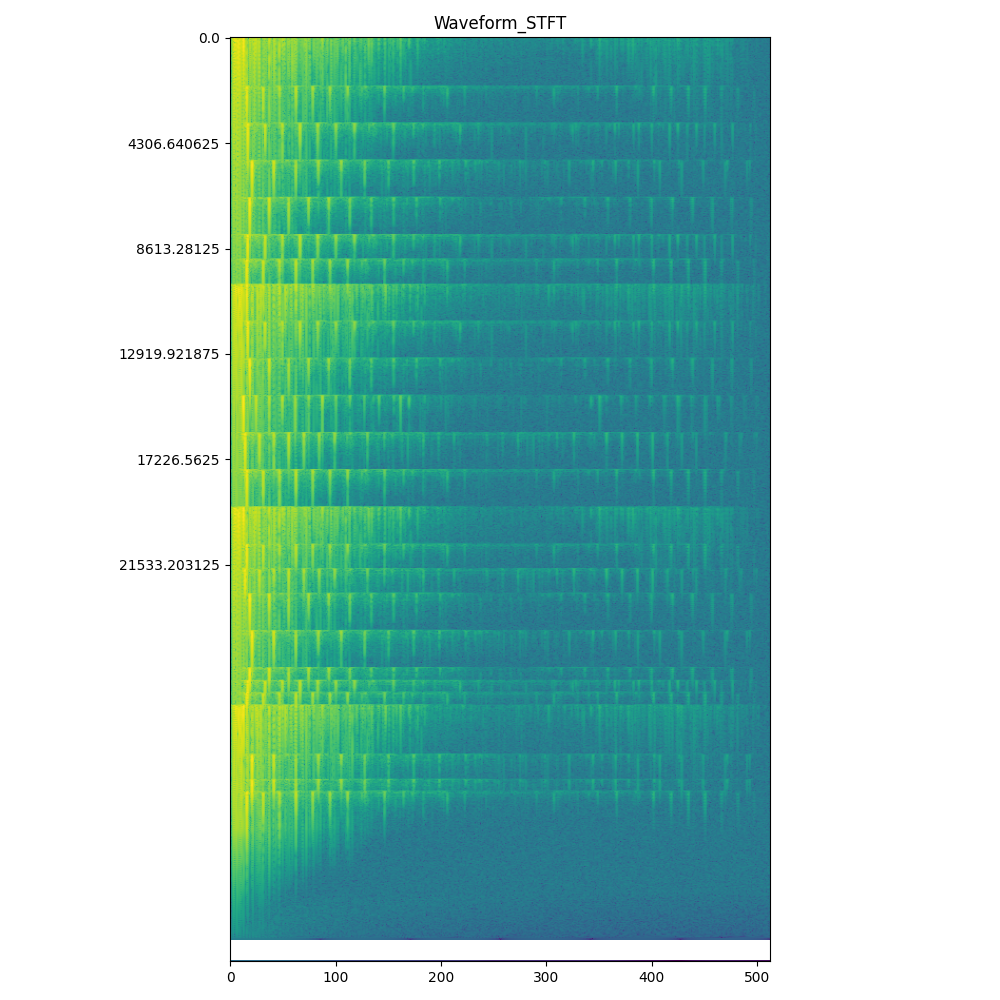
我们也可以使用librosa库提供的函数获取语谱图，代码如下：

# 语谱图
def plot_spectrogram(spectrogram, title="spectrogram(dB)"):
    plt.imshow(librosa.amplitude_to_db(spectrogram))
    plt.title(title)
    plt.xlabel("Frame/s")
    plt.ylabel("Frequency/hz")
    plt.colorbar()
    plt.show()
    
# 设置参数，调用librosa.stft函数
n_fft = 1024
hop_size = 512
waveform_stft = librosa.stft(y=waveform,n_fft=n_fft,hop_length=hop_size)
plot_spectrogram(np.abs(waveform_stft))

1.1.6 小波变换