目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

---

💥1 概述

1.1.算法简介

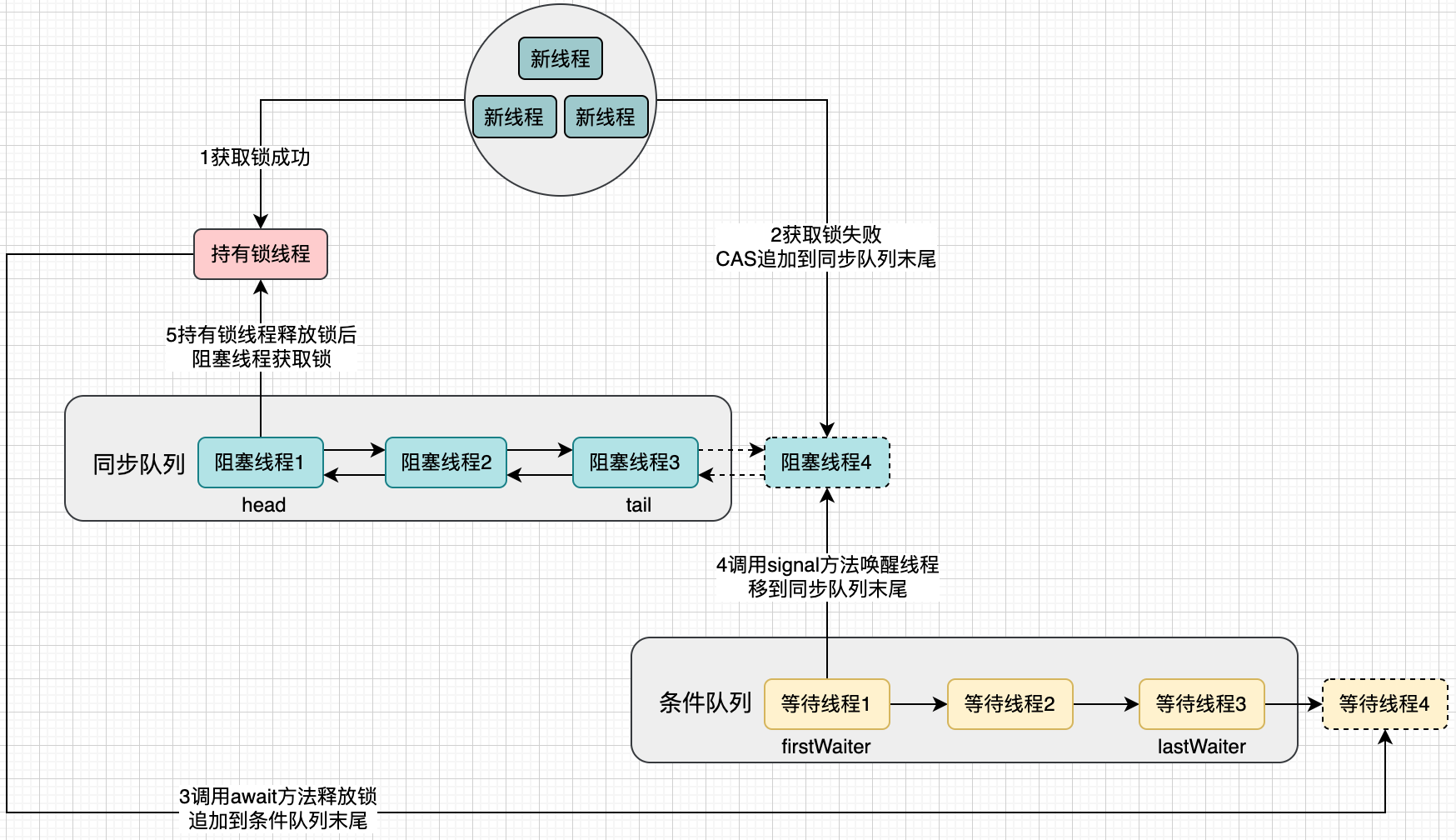
BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)。在模拟过程中收集系统所产生的误差，通过误差反传，然后调整权值大小，通过该不断迭代更新，最后使得模型趋于整体最优化（这是一个循环，我们在训练神经网络的时候是要不断的去重复这个过程的）。

BP神经网络具有以下优点：

1. 非线性映射能力：BP神经网络实质上实现了一个从输入到输出的映射功能，数学理论证明三层的神经网络就能够以任意精度逼近任何非线性连续函数。这使得其特别适合于求解内部机制复杂的问题，即BP神经网络具有较强的非线性映射能力。

2. 自学习和自适应能力：BP神经网络在训练时，能够通过学习自动提取输入、输出数据间的“合理规则”，并自适应地将学习内容记忆于网络的权值中。即BP神经网络具有高度自学习和自适应的能力。

3. 泛化能力：所谓泛化能力是指在设计模式分类器时，即要考虑网络在保证对所需分类对象进行正确分类，还要关心网络在经过训练后，能否对未见过的模式或有噪声污染的模式，进行正确的分类。也即BP神经网络具有将学习成果应用于新知识的能力。

BP神经网络具有以下缺点：

1. 局部极小化问题：从数学角度看，传统的 BP神经网络为一种局部搜索的优化方法，它要解决的是一个复杂非线性化问题，网络的权值是通过沿局部改善的方向逐渐进行调整的，这样会使算法陷入局部极值，权值收敛到局部极小点，从而导致网络训练失败。加上BP神经网络对初始网络权重非常敏感，以不同的权重初始化网络，其往往会收敛于不同的局部极小，这也是每次训练得到不同结果的根本原因。

2. BP 神经网络算法的收敛速度慢：由于BP神经网络算法本质上为梯度下降法，它所要优化的目标函数是非常复杂的，因此，必然会出现“锯齿形现象”，这使得BP算法低效；又由于优化的目标函数很复杂，它必然会在神经元输出接近0或1的情况下，出现一些平坦区，在这些区域内，权值误差改变很小，使训练过程几乎停顿；BP神经网络模型中，为了使网络执行BP算法，不能使用传统的一维搜索法求每次迭代的步长，而必须把步长的更新规则预先赋予网络，这种方法也会引起算法低效。以上种种，导致了BP神经网络算法收敛速度慢的现象。

3. BP 神经网络结构选择不一：BP神经网络结构的选择至今尚无一种统一而完整的理论指导，一般只能由经验选定。网络结构选择过大，训练中效率不高，可能出现过拟合现象，造成网络性能低，容错性下降，若选择过小，则又会造成网络可能不收敛。而网络的结构直接影响网络的逼近能力及推广性质。因此，应用中如何选择合适的网络结构是一个重要的问题。

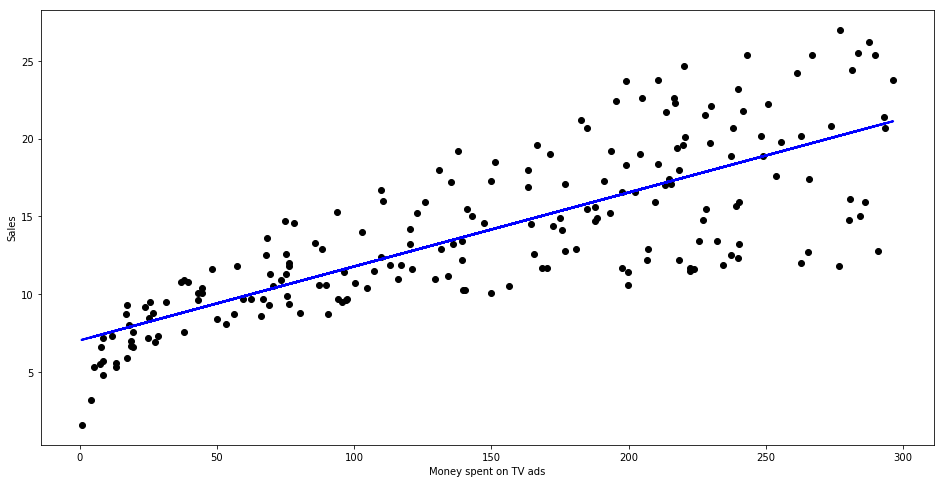
📚2 运行结果

主函数部分代码：

close all;

clear;

clc;

% the fundamental principle of the training is to run a feed-forward update

% and then apply backpropagation. (for each line of sample).

% A total iteration through all ~700 total records = 1 epoch.

rawData = load('rawdata.dt'); % first load the dataset:

maxRecords = size(rawData,1); % we know max number of records in the data is:

trainLimit = 350;

validationLimit=175;

testLimit=174;

% section the different data sets. OR pick randomly? probably better.

%trainingSet = rawData(1:trainLimit, 1:11);

%validationSet = rawData(trainLimit+1:trainLimit+validationLimit, 1:11);

%testSet = rawData(trainLimit+validationLimit+1:trainLimit+validationLimit+testLimit, 1:11);

% test the effect of learning rate.

    

for nHidNeuron = 6:6 % for no hidden neurons.

    acc = figure;

    SetGlobalHidden(nHidNeuron);

    

    maxEpochs = 30; % max Epochs to run.

    epochError = zeros(1, maxEpochs);

    avgTestScoreAtEpoch = zeros(1, maxEpochs);

    accuracyAtEpoch = zeros(1, maxEpochs);

    

    validationError = zeros(1, maxEpochs);

    initialError = 0;

    NN1 = NeuralNetwork(9,nHidNeuron,2); % create network.

    NN1.SetLearnRate(0.02);

    fprintf('== Initial Network ==\n');

    NN1.debugLayer(2);

    % before we run lets start timer.

    tTicker = tic;

    boolValidationBelowThreshold = false;

    

    if nHidNeuron > 4

        validationThreshold = 0.02; % only detect minima once we go lower than this.

    else

        validationThreshold = 0.07; %0.9;

    end

    

    

    for nEpoch = 0:maxEpochs

        sumE = 0;

        sumV = 0;

        randomRecord = 0;

        randomValidation = 0;

        for nRecord = 1:trainLimit

            %randomRecord = rawData(round(RangedRandom(1,trainLimit)),1:11);

            randomRecord = rawData(nRecord,1:11);

            

            if nEpoch > 0           

                % for every record feed forward and back-prop.

                NN1.Update(randomRecord); % forward update

                NN1.BackPropagate(randomRecord); % back-prop

            end

🎉3 参考文献

​[1]刘静. 一种改进的AdaBoost乳腺癌诊断模型[D].佛山科学技术学院,2020.DOI:10.27960/d.cnki.gfskj.2020.000037.

👨‍💻4 Matlab代码