【阿旭机器学习实战】系列文章主要介绍机器学习的各种算法模型及其实战案例，欢迎点赞，关注共同学习交流。

问题描述

你所在的公司在电视上做产品广告, 收集到了电视广告投入x(以百万为单位)与产品销售量y(以亿为单位)的数据. 你作为公司的数据科学家, 希望通过分析这些数据, 了解电视广告投入x(以百万为单位)与产品销售量y的关系.

假设x与y的之间的关系是线性的, 也就是说 y = ax + b. 通过线性回归(Linear Regression), 我们就可以得知 a 和 b 的值. 于是我们在未来做规划的时候, 通过电视广告投入x, 就可以预测产品销售量y, 从而可以提前做好生产和物流, 仓储的规划. 为客户提供更好的服务.

数据处理过程及源码

关注GZH：阿旭算法与机器学习，回复：“ML29”即可获取本文数据集、源码与项目文档，欢迎共同学习交流

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

data = pd.read_csv("./data/Advertising.csv")

data.head()

	TV	sales
0	230.1	22.1
1	44.5	10.4
2	17.2	9.3
3	151.5	18.5
4	180.8	12.9

data.columns

Index(['TV', 'sales'], dtype='object')

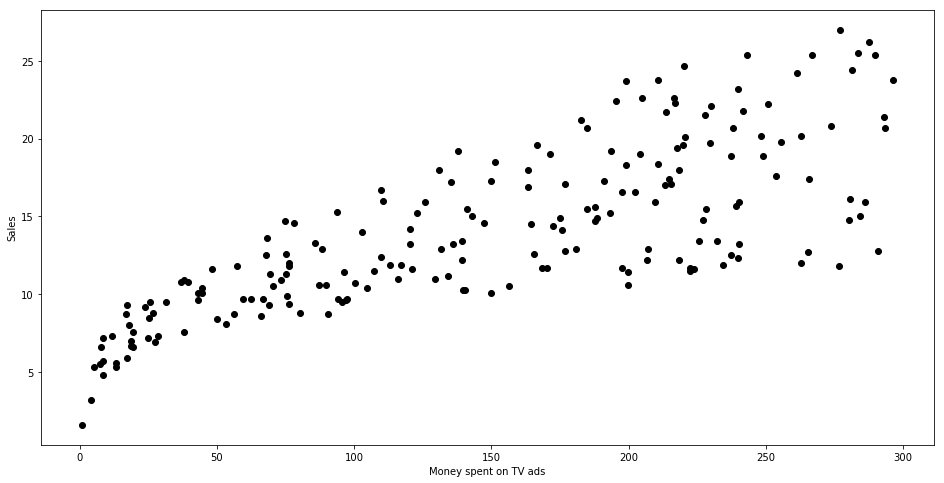
通过数据可视化分析数据

plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'], c ='black')
plt.xlabel("Money spent on TV ads")
plt.ylabel("Sales")
plt.show()

训练线性回归模型

X = data['TV'].values.reshape(-1,1)
y = data['sales'].values.reshape(-1,1)

reg = LinearRegression()
reg.fit(X, y)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
         normalize=False)

print('a = {:.5}'.format(reg.coef_[0][0]))
print('b = {:.5}'.format(reg.intercept_[0]))

print("线性模型为: Y = {:.5}X + {:.5} ".format(reg.coef_[0][0], reg.intercept_[0]))

a = 0.047537
b = 7.0326
线性模型为: Y = 0.047537X + 7.0326 

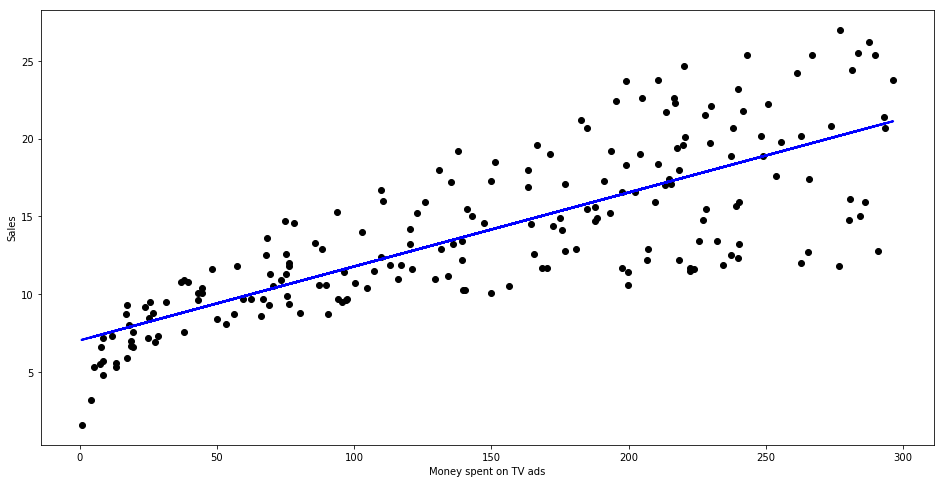
可视化训练好的线性回归模型

predictions = reg.predict(X)

plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'], c ='black')
plt.plot(data['TV'], predictions,c ='blue', linewidth=2)
plt.xlabel("Money spent on TV ads")
plt.ylabel("Sales")
plt.show()

结果预测

# 做预测
假设公司希望在下一个季度投一亿元的电视广告, 那么预期的产品销量会是多少呢?

predictions = reg.predict([[100])
print('投入一亿元的电视广告, 预计的销售量为{:.5}亿'.format( predictions[0][0]) )

投入一亿元的电视广告, 预计的销售量为11.786亿

如果内容对你有帮助，感谢点赞+关注哦！
更多干货内容持续更新中…

关注下方GZH：阿旭算法与机器学习，回复：“ML29”即可获取本文数据集、源码与项目文档，欢迎共同学习交流