【Redis】 数据结构：SDS、跳跃表等底层数据结构详解

参考资料：

带你看Redis数据结构底层系列-SDS

Redis—5种基本数据结构

Redis—跳跃表

图解 Redis 数据结构

Redis 常见数据类型和应用场景

Reids—神奇的HyperLoglog解决统计问题

面试杀手锏：Redis源码之SDS

面试杀手锏：Redis源码之BitMap

底层数据结构引入

在对对象机制（redisObject）有了初步认识之后，我们便可以继续理解如下的底层数据结构部分：

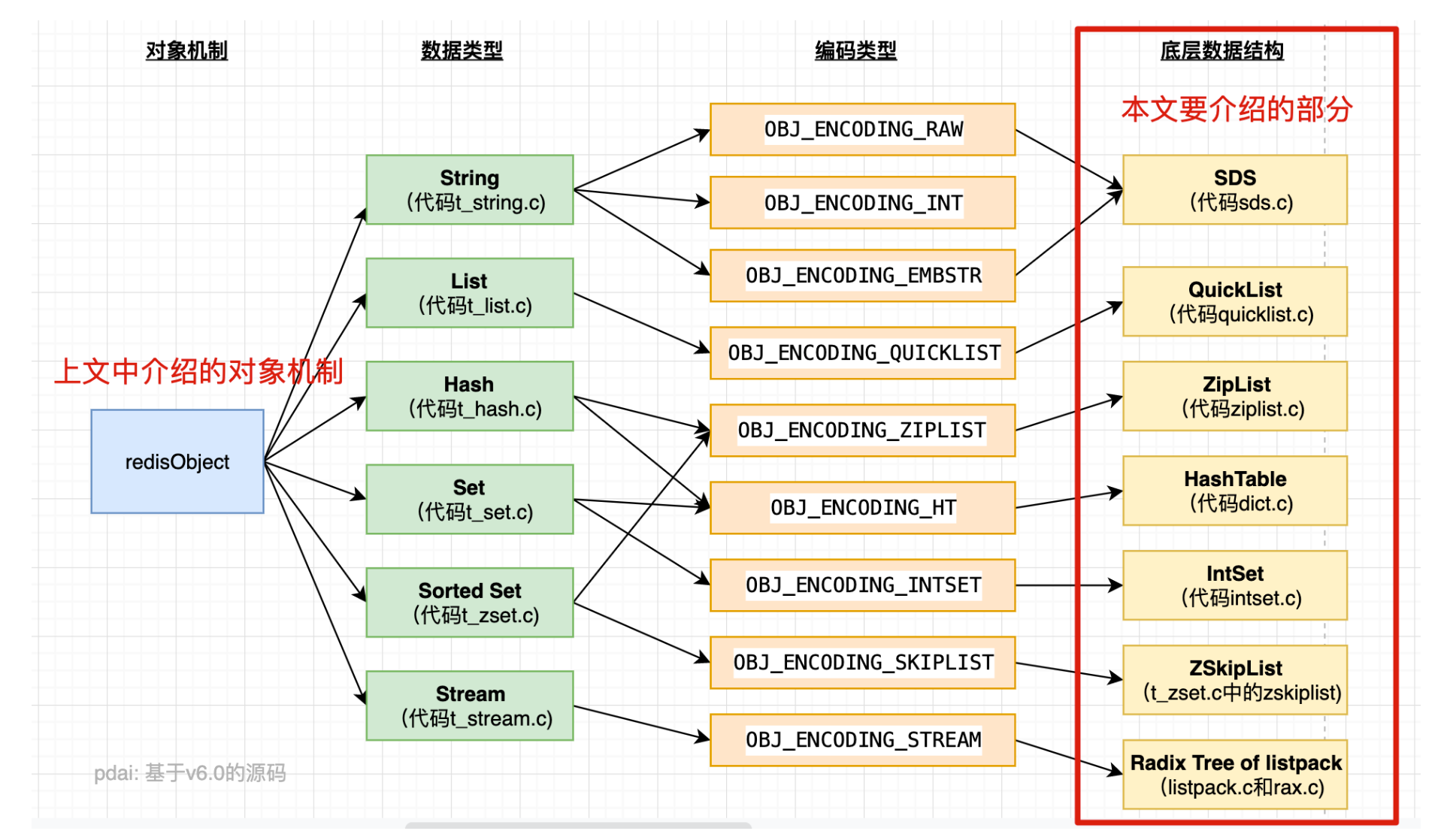
• 简单动态字符串 - sds
• 压缩列表 - ZipList
• 快表 - QuickList
• 字典/哈希表 - Dict
• 整数集 - IntSet
• 跳表 - ZSkipList

Redis数据结构 - 动态字符串 SDS

Redis 是用 C 语言写的，但是对于Redis的字符串，却不是 C 语言中的字符串（即以空字符’\0’结尾的字符数组），它是自己构建了一种名为 简单动态字符串（simple dynamic string,SDS）的抽象类型，并将 SDS 作为 Redis的默认字符串表示。

SDS 概述

这是一种用于存储二进制数据的一种结构, 具有动态扩容的特点. 其实现位于src/sds.h与src/sds.c中。

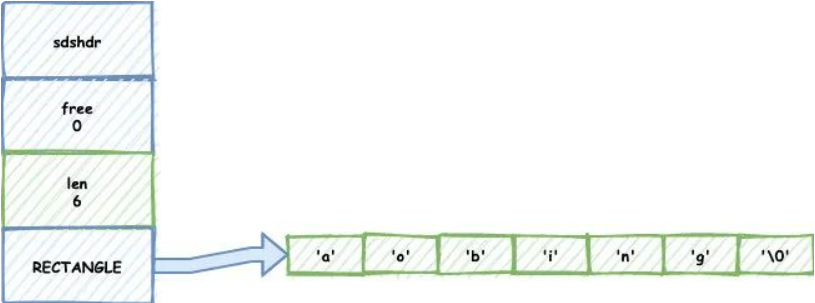
• SDS的总体概览如下图：

其中sdshdr是头部, buf是真实存储用户数据的地方. 另外注意, 从命名上能看出来, 这个数据结构除了能存储二进制数据, 显然是用于设计作为字符串使用的, 所以在buf中, 用户数据后总跟着一个\0. 即图中 "数据" + "\0"是为所谓的buf。

• Redis是C语言实现的，其中SDS是一个结构体，源码如下：

例如，一个包含字符串“name”的sds结构如下：

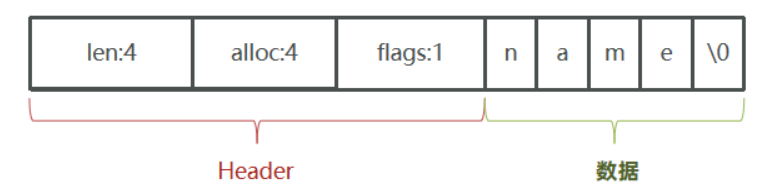
• 如下是6.0源码中sds相关的结构：

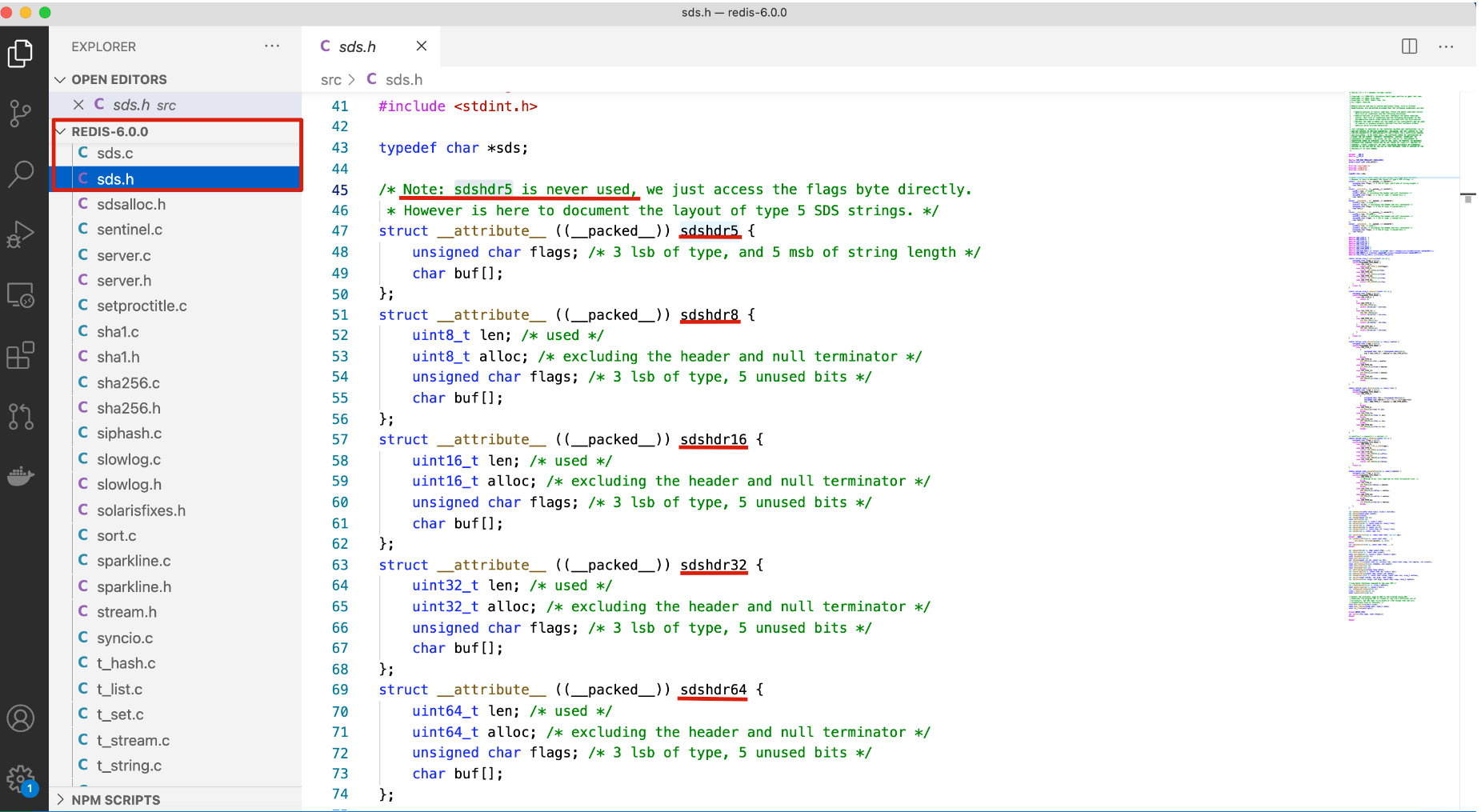
通过上图我们可以看到，SDS有五种不同的头部. 其中sdshdr5实际并未使用到. 所以实际上有四种不同的头部, 分别如下:

其中：

• len 保存了SDS保存字符串的长度
• buf[] 数组用来保存字符串的每个元素
• alloc分别以uint8, uint16, uint32, uint64表示整个SDS, 除过头部与末尾的\0, 剩余的字节数.
• flags 始终为一字节, 以低三位标示着头部的类型, 高5位未使用.

SDS动态扩容

SDS之所以叫做动态字符串，是因为它具备动态扩容的能力，例如一个内容为“hi”的SDS：

假如我们要给SDS追加一段字符串“,Amy”，这里首先会申请新内存空间：

• 如果新字符串小于1M，则新空间为扩展后字符串长度的两倍+1；

• 如果新字符串大于1M，则新空间为扩展后字符串长度+1M+1。称为内存预分配。

  

思考：这种分配策略会浪费内存资源吗？

答：执行过APPEND 命令的字符串会带有额外的预分配空间，这些预分配空间不会被释放，除非该字符串所对应的键被删除，或者等到关闭Redis 之后，再次启动时重新载入的字符串对象将不会有预分配空间。因为执行APPEND 命令的字符串键数量通常并不多，占用内存的体积通常也不大，所以这一般并不算什么问题。另一方面，如果执行APPEND 操作的键很多，而字符串的体积又很大的话，那可能就需要修改Redis 服务器，让它定时释放一些字符串键的预分配空间，从而更有效地使用内存。

为什么使用SDS

• 常数复杂度获取字符串长度

由于 len 属性的存在，我们获取 SDS 字符串的长度只需要读取 len 属性，时间复杂度为 O(1)。而对于 C 语言，获取字符串的长度通常是经过遍历计数来实现的，时间复杂度为 O(n)。通过 strlen key 命令可以获取 key 的字符串长度。

C语言对字符串长度的统计，就完全来自遍历，从头遍历到末尾，直到发现空字符就停止，以此统计出字符串的长度，这样获取长度的时间复杂度来说是0（n），大概就像下面这样：

但是这样的计数方式会留下隐患，所以Redis没有采用C的字符串，我后面会提到。

• 杜绝缓冲区溢出

我们知道在 C 语言中使用 strcat 函数来进行两个字符串的拼接，一旦没有分配足够长度的内存空间，就会造成缓冲区溢出。而对于 SDS 数据类型，在进行字符修改的时候，会首先根据记录的 len 属性检查内存空间是否满足需求，如果不满足，会进行相应的空间扩展，然后在进行修改操作，所以不会出现缓冲区溢出。

字符串拼接是我们经常做的操作，在C和Redis中一样，也是很常见的操作，但是问题就来了，C是不记录字符串长度的，一旦我们调用了拼接的函数，如果没有提前计算好内存，是会产生缓存区溢出的。

比如本来字符串长这样：

你现在需要在后面拼接 ，但是你没计算好内存，结果就可能这样了

• 减少修改字符串的内存重新分配次数

C语言由于不记录字符串的长度，所以如果要修改字符串，必须要重新分配内存（先释放再申请），因为如果没有重新分配，字符串长度增大时会造成内存缓冲区溢出，字符串长度减小时会造成内存泄露。

而对于SDS，由于len属性和alloc属性的存在，对于修改字符串SDS实现了空间预分配和惰性空间释放两种策略：

1、空间预分配：对字符串进行空 间扩展的时候，扩展的内存比实际需要的多，这样可以减少连续执行字符串增长操作所需的内存重分配次数。

比如现在有这样的一个字符：

我们调用了拼接函数，字符串边长了，Redis还会根据算法计算出一个free值给他备用：

我们再继续拼接，你会发现，备用的free用上了，省去了这次的内存重分配：

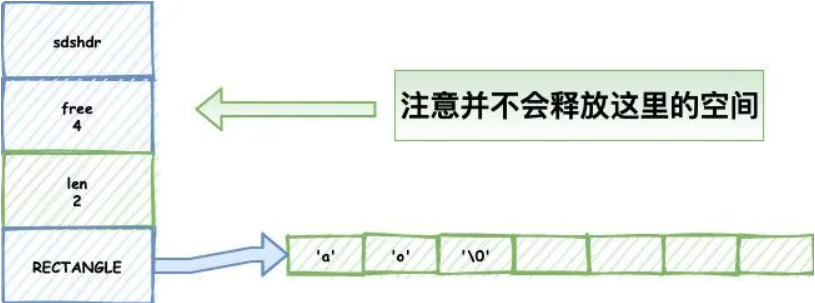
2、惰性空间释放：对字符串进行缩短操作时，程序不立即使用内存重新分配来回收缩短后多余的字节，而是使用 alloc 属性将这些字节的数量记录下来，等待后续使用。（当然SDS也提供了相应的API，当我们有需要时，也可以手动释放这些未使用的空间。）

还是一样的字符串：

当我们调用了删减的函数，并不会马上释放掉free空间：

如果我们需要继续添加这个空间就能用上了，减少了内存的重分配，如果空间不需要了，调用函数删掉就好了：

• 二进制安全

仔细看的仔肯定看到上面我不止一次提到了空字符也就是’\0‘，C语言是判断空字符去判断一个字符的长度的，但是有很多数据结构经常会穿插空字符在中间，比如图片，音频，视频，压缩文件的二进制数据，就比如下面这个单词，他只能识别前面的 不能识别后面的字符，那对于我们开发者而言，这样的结果显然不是我们想要的对不对。

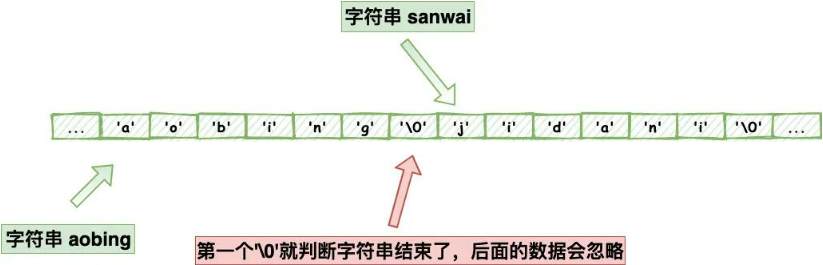
Redis就不存在这个问题了，他不是保存了字符串的长度嘛，他不判断空字符，他就判断长度对不对就好了，所以redis也经常被我们拿来保存各种二进制数据，我反正是用的很high，经常用来保存小文件的二进制。

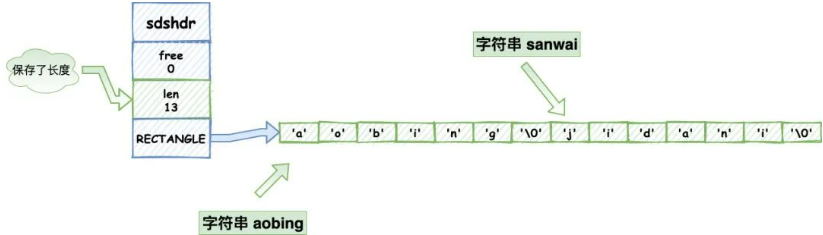
• 兼容部分 C 字符串函数

虽然 SDS 是二进制安全的，但是一样遵从每个字符串都是以空字符串结尾的惯例，这样可以重用 C 语言库<string.h> 中的一部分函数。

小结

redis的字符串表示为sds，而不是C字符串（以\0结尾的char*）， 它是Redis 底层所使用的字符串表示，它被用在几乎所有的Redis 模块中。可以看如下对比：

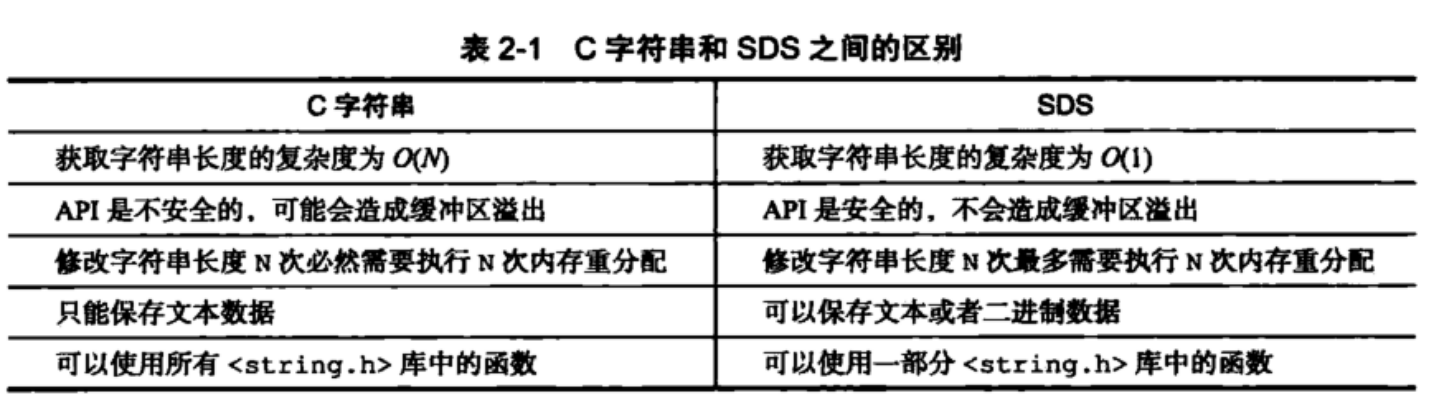
一般来说，SDS 除了保存数据库中的字符串值以外，SDS 还可以作为缓冲区（buffer）：包括 AOF 模块中的AOF缓冲区以及客户端状态中的输入缓冲区。

Redis数据结构 - 整数集 intset

IntSet概述

IntSet是Redis中set集合的一种实现方式，基于整数数组来实现，并且具备长度可变、有序等特征。结构如下：

typedef struct intset {
    uint32_t encoding;
    uint32_t length;
    int8_t contents[];
} intset;

• encoding 表示编码方式，的取值有三个：其中的encoding包含三种模式，表示存储的整数大小不同：

  • 

• length 代表其中存储的整数的个数

• contents 指向实际存储数值的连续内存区域, 就是一个数组；整数集合的每个元素都是 contents 数组的一个数组项（item），各个项在数组中按值得大小从小到大有序排序，且数组中不包含任何重复项。（虽然 intset 结构将 contents 属性声明为 int8_t 类型的数组，但实际上 contents 数组并不保存任何 int8_t 类型的值，contents 数组的真正类型取决于 encoding 属性的值）

内存布局图

其内存布局如下图所示:

我们可以看到，content数组里面每个元素的数据类型是由encoding来决定的，那么如果原来的数据类型是int16, 当我们再插入一个int32类型的数据时怎么办呢？这就是下面要说的intset的升级。

IntSet的升级

为了方便查找，Redis会将intset中所有的整数按照升序依次保存在contents数组中，结构如图：

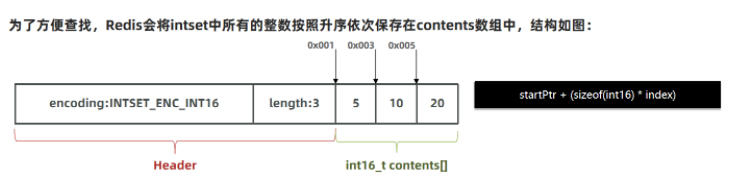
现在，数组中每个数字都在int16_t的范围内，因此采用的编码方式是INTSET_ENC_INT16，每部分占用的字节大小为：

• encoding：4字节
• length：4字节
• contents：2字节 * 3 = 6字节

我们向该其中添加一个数字：50000，这个数字超出了int16_t的范围，intset会自动升级编码方式到合适的大小。

整个过程有三步：

• 根据新元素的类型（比如int32），扩展整数集合底层数组的空间大小，并为新元素分配空间。

• 将底层数组现有的所有元素都转换成与新元素相同的类型， 并将类型转换后的元素放置到正确的位上， 而且在放置元素的过程中， 需要继续维持底层数组的有序性质不变。

• 最后改变encoding的值，length+1。

那么如果我们删除掉刚加入的 50000 时，会不会做一个降级操作呢？

• 不会。主要还是减少开销的权衡。

升级源码如下：

小结

Intset可以看做是特殊的整数数组，具备一些特点：

• Redis会确保Intset中的元素唯一、有序
• 具备类型升级机制，可以节省内存空间
• 底层采用二分查找方式来查询

Redis数据结构 - 字典/哈希表 Dict

Dict概述

我们知道Redis是一个键值型（Key-Value Pair）的数据库，我们可以根据键实现快速的 增删改查。而键与值的映射关系正是通过Dict来实现的。

Dict由三部分组成，分别是：哈希表（DictHashTable）、哈希节点（DictEntry）、字典（Dict）

添加元素过程

当我们向Dict添加键值对时，Redis首先根据key计算出hash值（h），然后利用 h & sizemask来计算元素应该存储到数组中的哪个索引位置。我们存储k1=v1，假设k1的哈希值h =1，则1&3 =1，因此k1=v1要存储到数组角标1位置。

解决哈希冲突

注意这里还有一个指向下一个哈希表节点的指针，我们知道哈希表最大的问题是存在哈希冲突，如何解决哈希冲突，有开放地址法和链地址法。这里采用的便是链地址法，通过next这个指针可以将多个哈希值相同的键值对连接在一起，用来解决哈希冲突。

Dict的扩容

Dict中的HashTable就是数组结合单向链表的实现，当集合中元素较多时，必然导致哈希冲突增多，链表过长，则查询效率会大大降低。
Dict在每次新增键值对时都会检查负载因子 ，满足以下两种情况时会触发哈希表扩容：

• 触发扩容的条件：

1、服务器目前没有执行 BGSAVE 命令或者 BGREWRITEAOF 命令，并且负载因子大于等于1。

2、服务器目前正在执行 BGSAVE 命令或者 BGREWRITEAOF 命令，并且负载因子大于等于5。

ps：负载因子 = 哈希表已保存节点数量 / 哈希表大小。

Dict的rehash

不管是扩容还是收缩，必定会创建新的哈希表，导致哈希表的size和sizemask变化，而key的查询与sizemask有关。因此必须对哈希表中的每一个key重新计算索引，插入新的哈希表，这个过程称为rehash。过程是这样的：

• 当前状态

• 计算新hash表的realeSize，值取决于当前要做的是扩容还是收缩：

  

  • 如果是扩容，则新size为第一个大于等于dict.ht[0].used + 1的2^n
  • 如果是收缩，则新size为第一个大于等于dict.ht[0].used的2^n （不得小于4）

• 按照新的realeSize申请内存空间，创建dictht，并赋值给dict.ht[1]

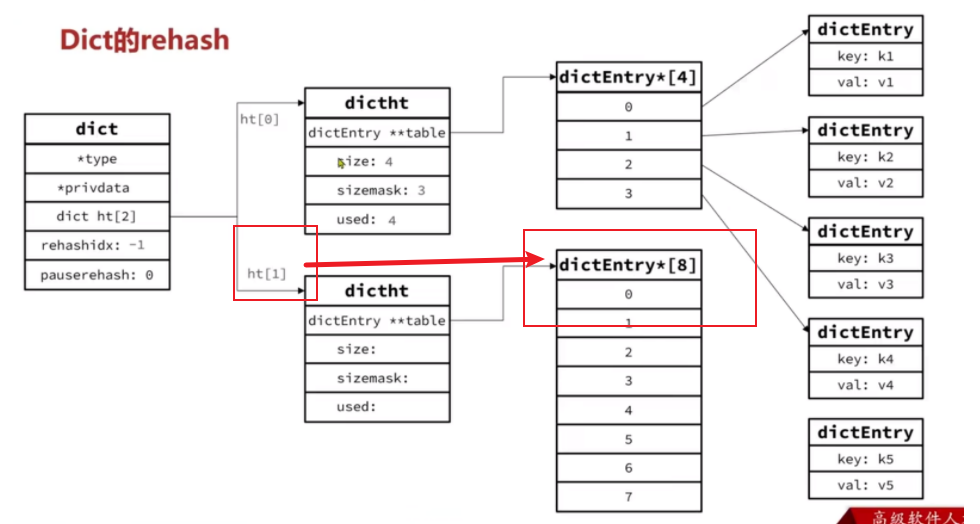
• 设置dict.rehashidx = 0，标示开始rehash

  

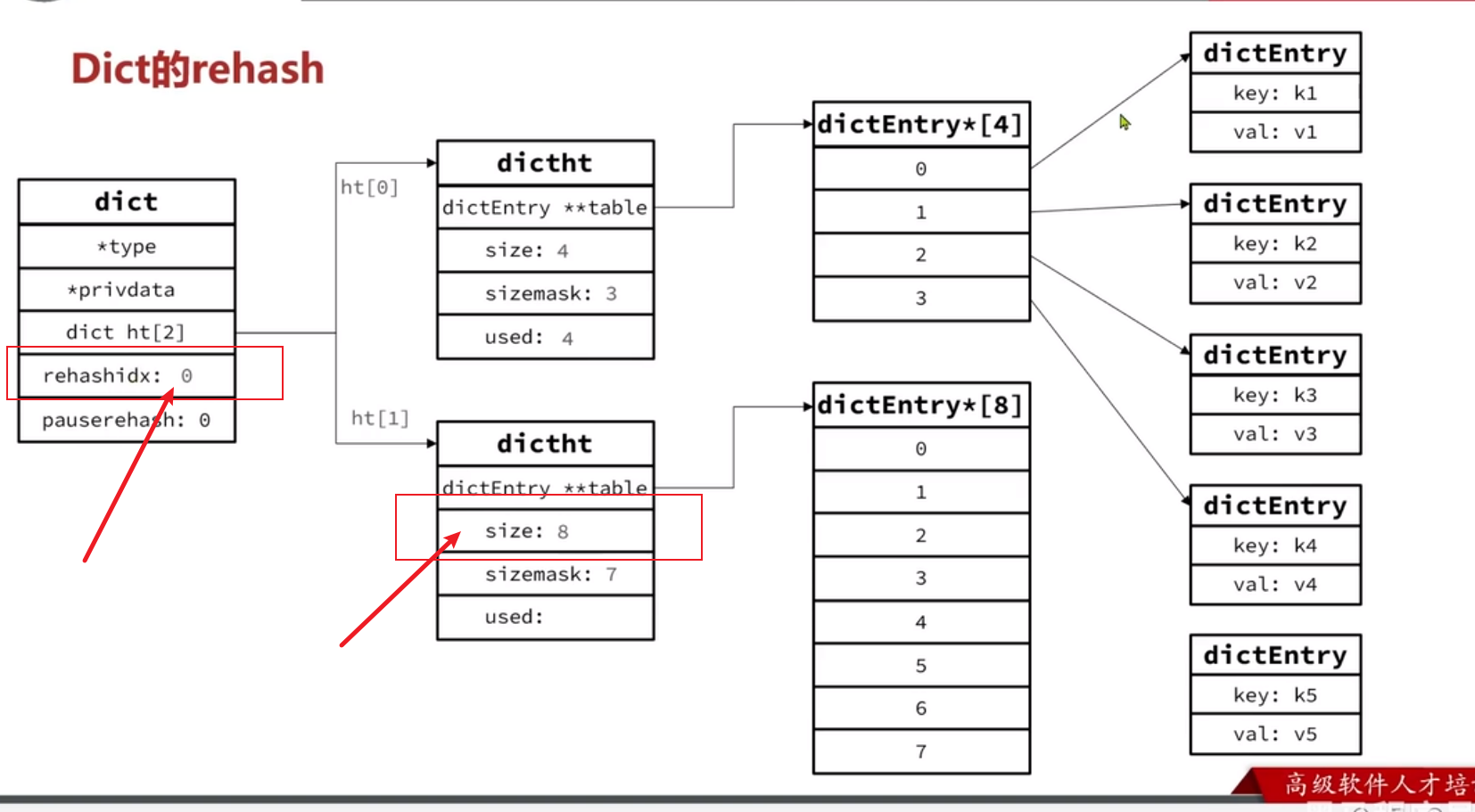
• 将dict.ht[0]中的每一个dictEntry都rehash到dict.ht[1]

• 

• 将dict.ht[1]赋值给dict.ht[0]，给dict.ht[1]初始化为空哈希表，释放原来的dict.ht[0]的内存

  

  

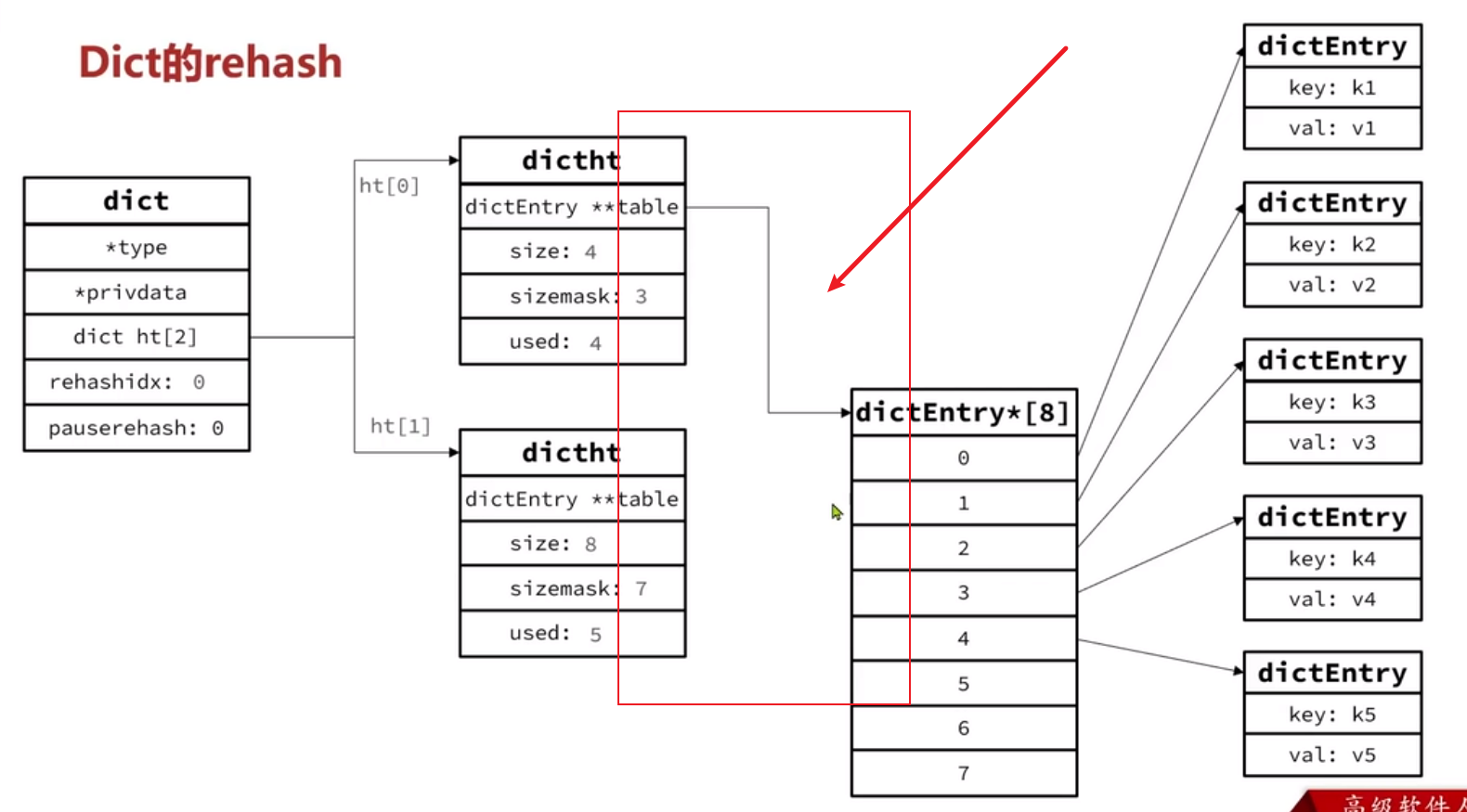
• 将rehashidx赋值为-1，代表rehash结束

  

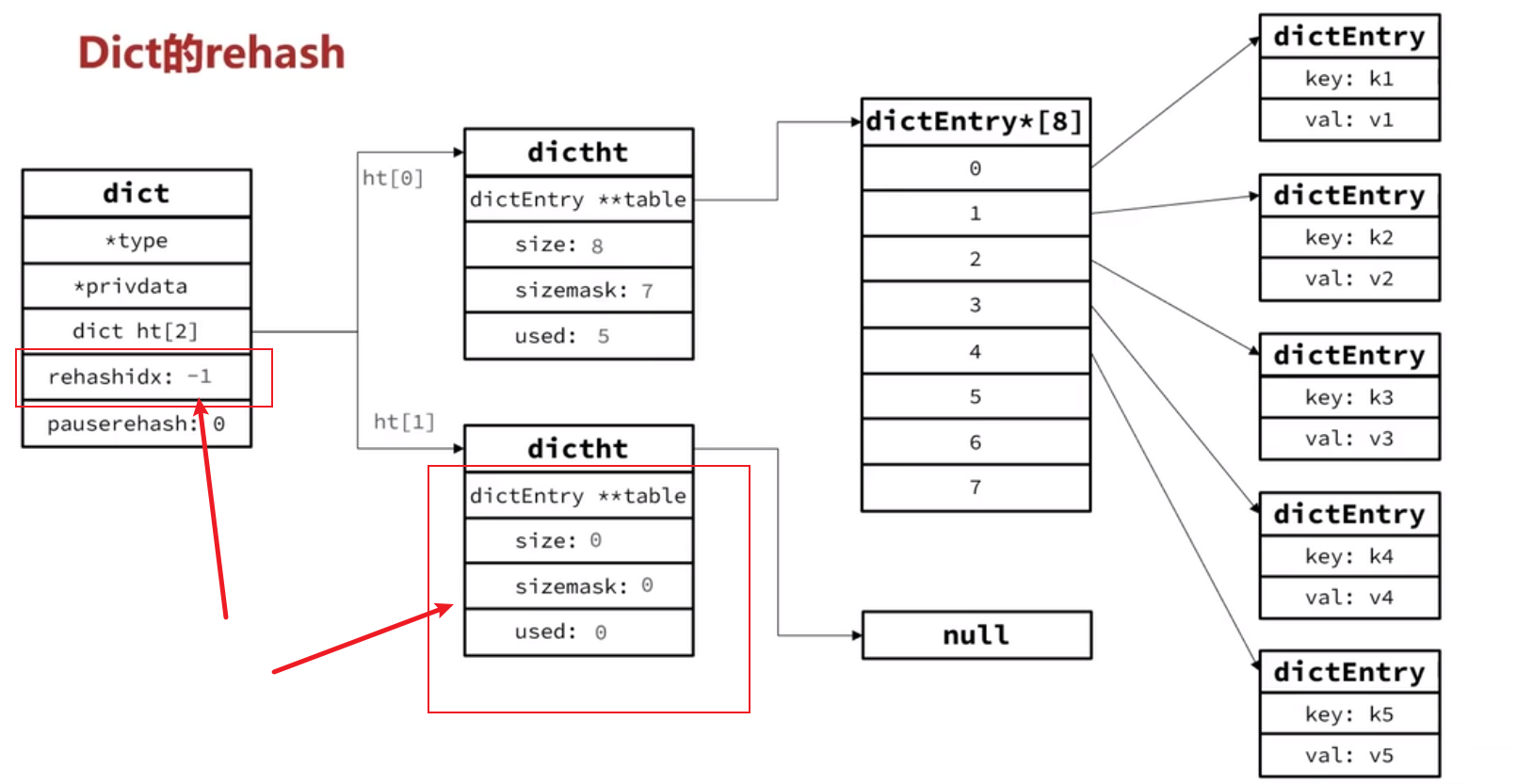
• 在rehash过程中，新增操作，则直接写入ht[1]，查询、修改和删除则会在dict.ht[0]和dict.ht[1]依次查找并执行。这样可以确保ht[0]的数据只减不增，随着rehash最终为空

渐近式 rehash

什么叫渐进式 rehash？也就是说扩容和收缩操作不是一次性、集中式完成的，而是分多次、渐进式完成的。如果保存在Redis中的键值对只有几个几十个，那么 rehash 操作可以瞬间完成，但是如果键值对有几百万，几千万甚至几亿，那么要一次性的进行 rehash，势必会造成Redis一段时间内不能进行别的操作。所以Redis采用渐进式 rehash,这样在进行渐进式rehash期间，字典的删除查找更新等操作可能会在两个哈希表上进行，第一个哈希表没有找到，就会去第二个哈希表上进行查找。但是进行 增加操作，一定是在新的哈希表上进行的。

Redis数据结构 - 压缩列表 ZipList

ZipList概述

ZipList 是一种特殊的“双端链表” ，由一系列特殊编码的连续内存块组成。可以在任意一端进行压入/弹出操作, 并且该操作的时间复杂度为 O(1)。

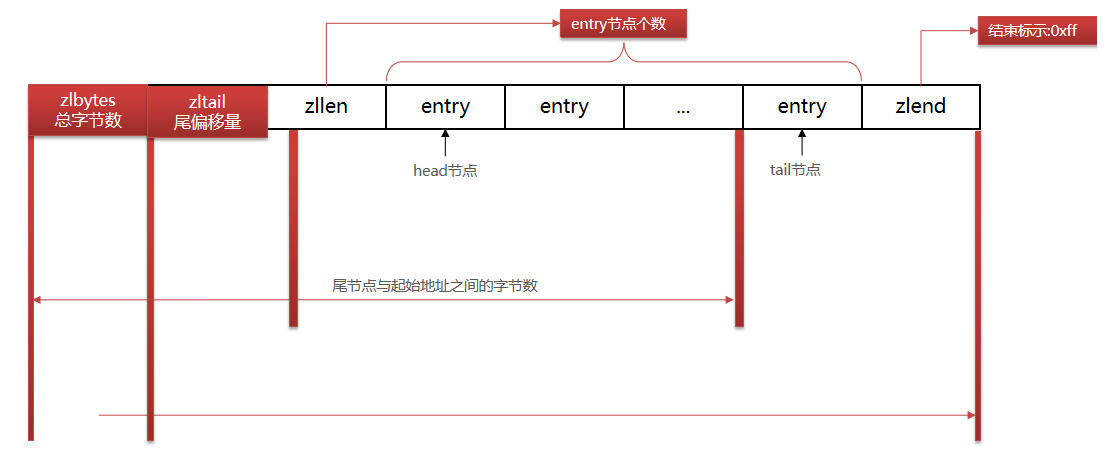
属性	类型	长度	用途
zlbytes	uint32_t	4 字节	记录整个压缩列表占用的内存字节数
zltail	uint32_t	4 字节	记录压缩列表表尾节点距离压缩列表的起始地址有多少字节，通过这个偏移量，可以确定表尾节点的地址。
zllen	uint16_t	2 字节	记录了压缩列表包含的节点数量。 最大值为UINT16_MAX （65534），如果超过这个值，此处会记录为65535，但节点的真实数量需要遍历整个压缩列表才能计算得出。
entry	列表节点	不定	压缩列表包含的各个节点，节点的长度由节点保存的内容决定。
zlend	uint8_t	1 字节	特殊值 0xFF （十进制 255 ），用于标记压缩列表的末端。

ZipListEntry概述

ZipList 中的Entry并不像普通链表那样记录前后节点的指针，因为记录两个指针要占用16个字节，浪费内存。而是采用了下面的结构：

• previous_entry_length：前一节点的长度，占1个或5个字节。

  • 如果前一节点的长度小于254字节，则采用1个字节来保存这个长度值
  • 如果前一节点的长度大于254字节，则采用5个字节来保存这个长度值，第一个字节为0xfe，后四个字节才是真实长度数据

• encoding：编码属性，记录content的数据类型（字符串还是整数）以及长度，占用1个、2个或5个字节

• contents：负责保存节点的数据，可以是字符串或整数

ZipList中所有存储长度的数值均采用小端字节序，即低位字节在前，高位字节在后。例如：数值0x1234，采用小端字节序后实际存储值为：0x3412

Encoding编码

ZipListEntry中的encoding编码分为字符串和整数两种：
字符串：如果encoding是以“00”、“01”或者“10”开头，则证明content是字符串

编码	编码长度	字符串大小
|00pppppp|	1 bytes	<= 63 bytes
|01pppppp|qqqqqqqq|	2 bytes	<= 16383 bytes
|10000000|qqqqqqqq|rrrrrrrr|ssssssss|tttttttt|	5 bytes	<= 4294967295 bytes

例如，我们要保存字符串：“ab”和 “bc”

ZipListEntry中的encoding编码分为字符串和整数两种：

• 整数：如果encoding是以“11”开始，则证明content是整数，且encoding固定只占用1个字节

编码	编码长度	整数类型
11000000	1	int16_t（2 bytes）
11010000	1	int32_t（4 bytes）
11100000	1	int64_t（8 bytes）
11110000	1	24位有符整数(3 bytes)
11111110	1	8位有符整数(1 bytes)
1111xxxx	1	直接在xxxx位置保存数值，范围从0001~1101，减1后结果为实际值

为什么ZipList特别省内存

• ziplist节省内存是相对于普通的list来说的，如果是普通的数组，那么它每个元素占用的内存是一样的且取决于最大的那个元素（很明显它是需要预留空间的）；
• 所以ziplist在设计时就很容易想到要尽量让每个元素按照实际的内容大小存储，所以增加encoding字段，针对不同的encoding来细化存储大小；
• 这时候还需要解决的一个问题是遍历元素时如何定位下一个元素呢？在普通数组中每个元素定长，所以不需要考虑这个问题；但是ziplist中每个data占据的内存不一样，所以为了解决遍历，需要增加记录上一个元素的length，所以增加了prelen字段。

为什么我们去研究ziplist特别节省内存的数据结构？ 在实际应用中，大量存储字符串的优化是需要你对底层的数据结构有一定的理解的，而ziplist在场景优化的时候也被考虑采用的首选。

ZipList的连锁更新问题

ZipList的每个Entry都包含previous_entry_length来记录上一个节点的大小，长度是1个或5个字节：
如果前一节点的长度小于254字节，则采用1个字节来保存这个长度值
如果前一节点的长度大于等于254字节，则采用5个字节来保存这个长度值，第一个字节为0xfe，后四个字节才是真实长度数据
现在，假设我们有N个连续的、长度为250~253字节之间的entry，因此entry的previous_entry_length属性用1个字节即可表示，如图所示：

ZipList这种特殊情况下产生的连续多次空间扩展操作称之为连锁更新（Cascade Update）。新增、删除都可能导致连锁更新的发生。

Ziplist的缺点

• ziplist也不预留内存空间, 并且在移除结点后, 也是立即缩容, 这代表每次写操作都会进行内存分配操作。
• 结点如果扩容, 导致结点占用的内存增长, 并且超过254字节的话, 可能会导致链式反应: 其后一个结点的entry.prevlen需要从一字节扩容至五字节. 最坏情况下, 第一个结点的扩容, 会导致整个ziplist表中的后续所有结点的entry.prevlen字段扩容. 虽然这个内存重分配的操作依然只会发生一次, 但代码中的时间复杂度是o(N)级别, 因为链式扩容只能一步一步的计算. 但这种情况的概率十分的小, 一般情况下链式扩容能连锁反映五六次就很不幸了. 之所以说这是一个蛋疼问题, 是因为, 这样的坏场景下, 其实时间复杂度并不高: 依次计算每个entry新的空间占用, 也就是o(N), 总体占用计算出来后, 只执行一次内存重分配, 与对应的memmove操作, 就可以了。

ZipList总结

ZipList特性：

• 压缩列表的可以看做一种连续内存空间的"双向链表"
• 列表的节点之间不是通过指针连接，而是记录上一节点和本节点长度来寻址，内存占用较低
• 如果列表数据过多，导致链表过长，可能影响查询性能
• 增或删较大数据时有可能发生连续更新问题

Redis数据结构 - 快表 QuickList

quicklist这个结构是Redis在3.2版本后新加的, 之前的版本是list(即linkedlist)， 用于String数据类型中。

QuickList引入

• ZipList虽然节省内存，但申请内存必须是连续空间，如果内存占用较多，申请内存效率很低。怎么办？

​ 答：为了缓解这个问题，我们必须限制ZipList的长度和entry大小。

• 但是我们要存储大量数据，超出了ZipList最佳的上限该怎么办？

​ 答：我们可以创建多个ZipList来分片存储数据。

• 数据拆分后比较分散，不方便管理和查找，这多个ZipList如何建立联系？

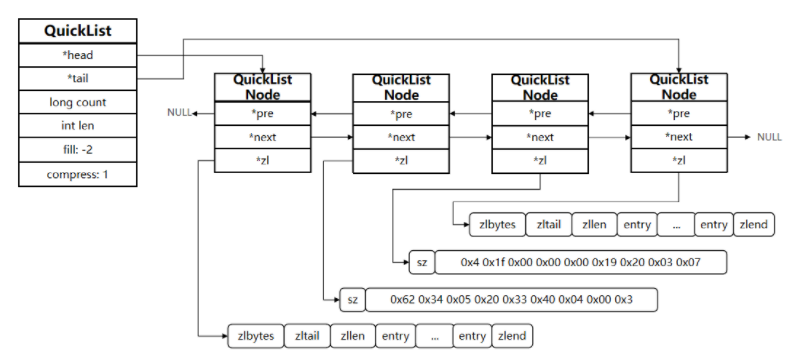
​ 答：Redis在3.2版本引入了新的数据结构QuickList，它是一个双端链表，只不过链表中的每个节点都是一个ZipList。

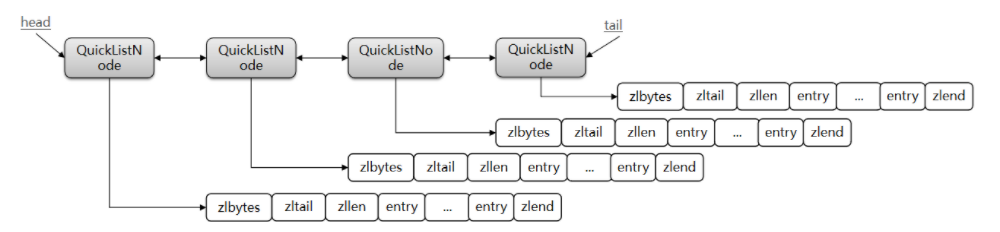
QuickList内存布局图

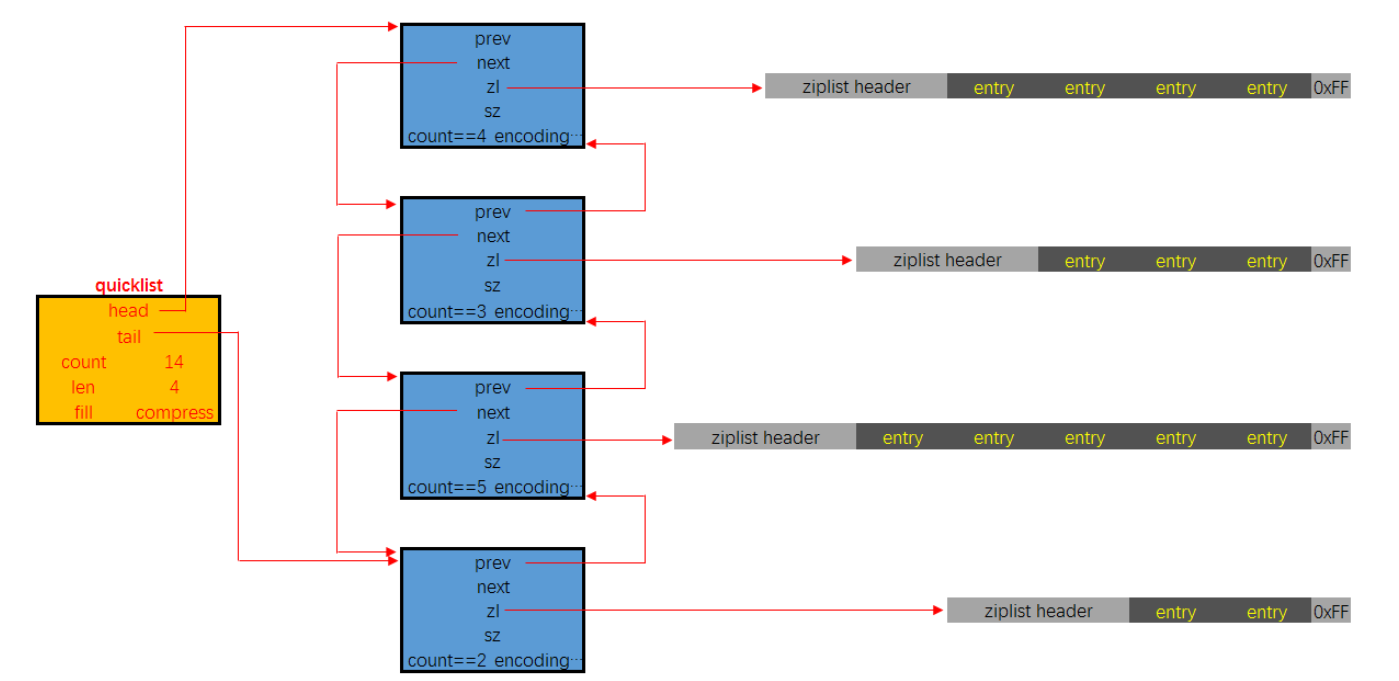
以下是QuickList的和QuickListNode的结构源码：

我们接下来用一段流程图来描述当前的这个结构

QuickList更多额外信息

为了避免QuickList中的每个ZipList中entry过多，Redis提供了一个配置项：list-max-ziplist-size来限制。
如果值为正，则代表ZipList的允许的entry个数的最大值
如果值为负，则代表ZipList的最大内存大小，分5种情况：

• -1：每个ZipList的内存占用不能超过4kb
• -2：每个ZipList的内存占用不能超过8kb
• -3：每个ZipList的内存占用不能超过16kb
• -4：每个ZipList的内存占用不能超过32kb
• -5：每个ZipList的内存占用不能超过64kb

其默认值为 -2：

QuickList总结

QuickList的特点：

• 是一个节点为ZipList的双端链表
• 节点采用ZipList，解决了传统链表的内存占用问题
• 控制了ZipList大小，解决连续内存空间申请效率问题
• 中间节点可以压缩，进一步节省了内存

Redis数据结构 - 跳跃表 SkipList

跳跃表概述

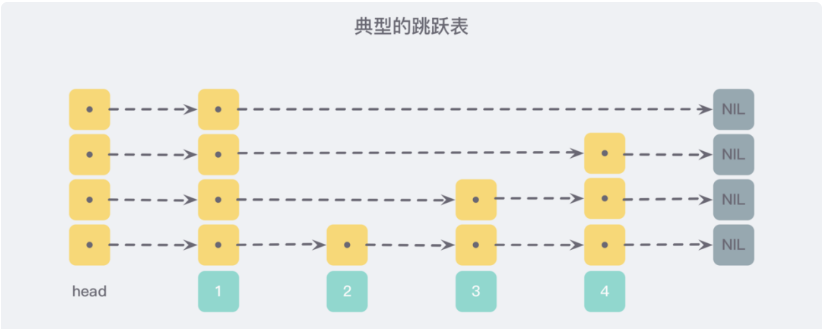
SkipList（跳表）首先是链表，但与传统链表相比有几点差异：
元素按照升序排列存储
节点可能包含多个指针，指针跨度不同。

为什么使用跳跃表

首先，因为 zset 要支持随机的插入和删除，所以它 不宜使用数组来实现，关于排序问题，我们也很容易就想到 红黑树/ 平衡树 这样的树形结构，为什么 Redis 不使用这样一些结构呢？

1. 性能考虑： 在高并发的情况下，树形结构需要执行一些类似于 rebalance 这样的可能涉及整棵树的操作，相对来说跳跃表的变化只涉及局部 (下面详细说)；
2. 实现考虑： 在复杂度与红黑树相同的情况下，跳跃表实现起来更简单，看起来也更加直观；

基于以上的一些考虑，Redis 基于 William Pugh 的论文做出一些改进后采用了 跳跃表 这样的结构。

本质是解决查找问题

我们先来看一个普通的链表结构：

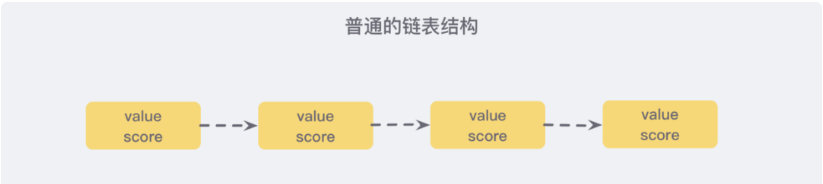
我们需要这个链表按照 score 值进行排序，这也就意味着，当我们需要添加新的元素时，我们需要定位到插入点，这样才可以继续保证链表是有序的，通常我们会使用 二分查找法，但二分查找是有序数组的，链表没办法进行位置定位，我们除了遍历整个找到第一个比给定数据大的节点为止 （时间复杂度 O(n)) 似乎没有更好的办法。

但假如我们每相邻两个节点之间就增加一个指针，让指针指向下一个节点，如下图：

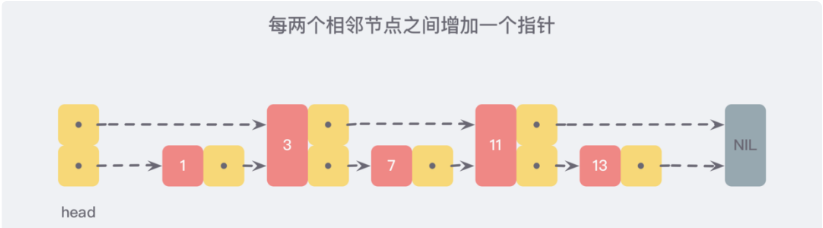
这样所有新增的指针连成了一个新的链表，但它包含的数据却只有原来的一半 （图中的为 3，11）。

现在假设我们想要查找数据时，可以根据这条新的链表查找，如果碰到比待查找数据大的节点时，再回到原来的链表中进行查找，比如，我们想要查找 7，查找的路径则是沿着下图中标注出的红色指针所指向的方向进行的：

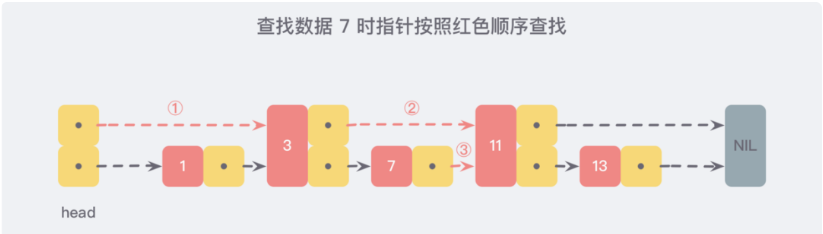
这是一个略微极端的例子，但我们仍然可以看到，通过新增加的指针查找，我们不再需要与链表上的每一个节点逐一进行比较，这样改进之后需要比较的节点数大概只有原来的一半。

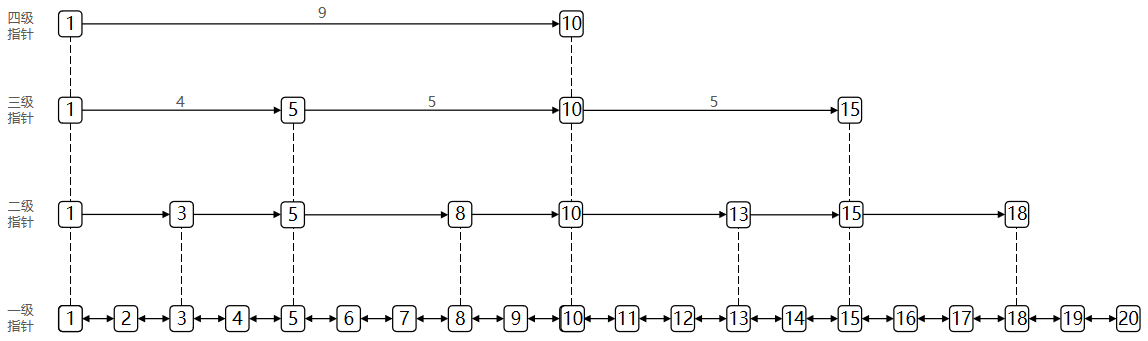
利用同样的方式，我们可以在新产生的链表上，继续为每两个相邻的节点增加一个指针，从而产生第三层链表：

在这个新的三层链表结构中，我们试着 查找 13，那么沿着最上层链表首先比较的是 11，发现 11 比 13 小，于是我们就知道只需要到 11 后面继续查找，从而一下子跳过了 11 前面的所有节点。

可以想象，当链表足够长，这样的多层链表结构可以帮助我们跳过很多下层节点，从而加快查找的效率。

更进一步的跳跃表

跳跃表 skiplist 就是受到这种多层链表结构的启发而设计出来的。按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似于一个二分查找，使得查找的时间复杂度可以降低到 O(logn)。

但是，这种方法在插入数据的时候有很大的问题。新插入一个节点之后，就会打乱上下相邻两层链表上节点个数严格的 2:1 的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点 （也包括新插入的节点） 重新进行调整，这会让时间复杂度重新蜕化成 O(n)。删除数据也有同样的问题。

skiplist 为了避免这一问题，它不要求上下相邻两层链表之间的节点个数有严格的对应关系，而是 为每个节点随机出一个层数(level)。比如，一个节点随机出的层数是 3，那么就把它链入到第 1 层到第 3 层这三层链表中。为了表达清楚，下图展示了如何通过一步步的插入操作从而形成一个 skiplist 的过程：

从上面的创建和插入的过程中可以看出，每一个节点的层数（level）是随机出来的，而且新插入一个节点并不会影响到其他节点的层数，因此，插入操作只需要修改节点前后的指针，而不需要对多个节点都进行调整，这就降低了插入操作的复杂度。

现在我们假设从我们刚才创建的这个结构中查找 23 这个不存在的数，那么查找路径会如下图：

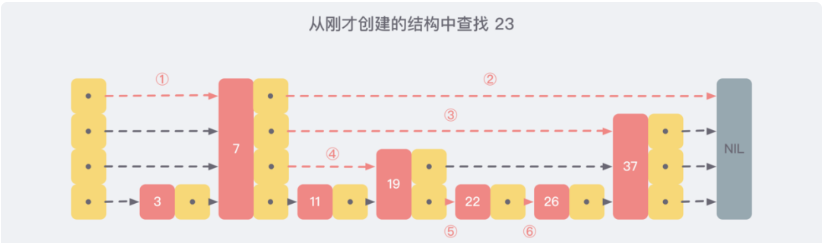
跳跃表的实现

Redis—跳跃表

SkipList的设计

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned int span;
    } level[];
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

其内存布局如下图:

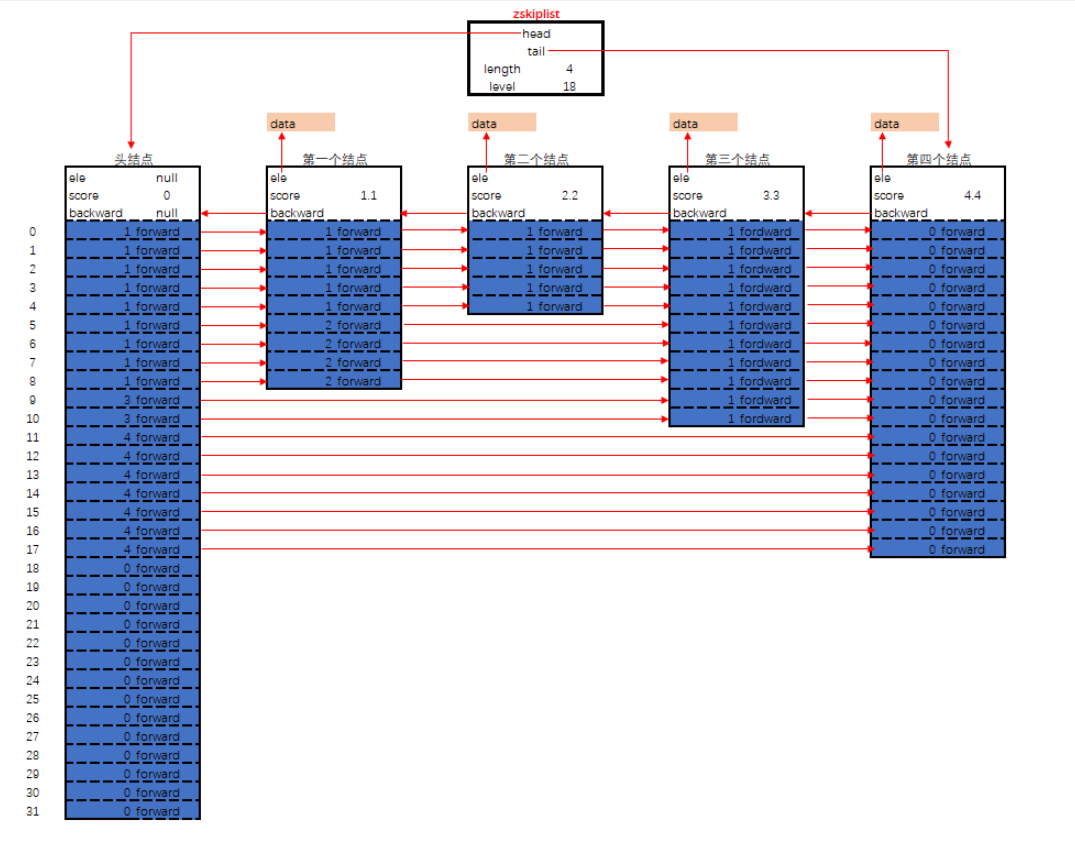
zskiplist的核心设计要点

• 头节点不持有任何数据, 且其level[]的长度为32
• 每个结点
  • ele字段，持有数据，是sds类型
  • score字段, 其标示着结点的得分, 结点之间凭借得分来判断先后顺序, 跳跃表中的结点按结点的得分升序排列.
  • backward指针, 这是原版跳跃表中所没有的. 该指针指向结点的前一个紧邻结点.
  • level字段, 用以记录所有结点(除过头节点外)；每个结点中最多持有32个zskiplistLevel结构. 实际数量在结点创建时, 按幂次定律随机生成(不超过32). 每个zskiplistLevel中有两个字段
    • forward字段指向比自己得分高的某个结点(不一定是紧邻的), 并且, 若当前zskiplistLevel实例在level[]中的索引为X, 则其forward字段指向的结点, 其level[]字段的容量至少是X+1. 这也是上图中, 为什么forward指针总是画的水平的原因.
    • span字段代表forward字段指向的结点, 距离当前结点的距离. 紧邻的两个结点之间的距离定义为1

SkipList总结

SkipList的特点：

• 跳跃表是一个双向链表，每个节点都包含score和ele值
• 节点按照score值排序，score值一样则按照ele字典排序
• 每个节点都可以包含多层指针，层数是1到32之间的随机数
• 不同层指针到下一个节点的跨度不同，层级越高，跨度越大
• 增删改查效率与红黑树基本一致，实现却更简单