1.数理逻辑
2. 集合论
3. 代数系统
4. 图论
图:点+边+边与点的映射函数
连通性与判别
欧拉图与哈密尔顿图
二分图和平面图与欧拉公式
树及生成树
单源点最短路径:Dijkstra算法
对偶图
4. 图论
4.1 图的基本概念
4.1.1 图
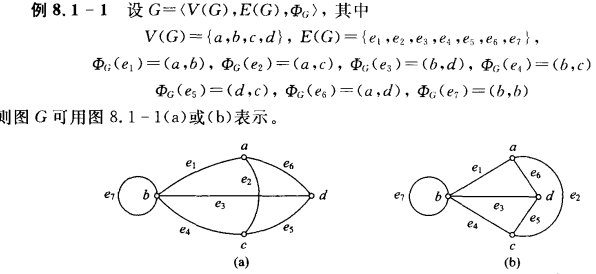
一个图G是一个三重组 < V ( G ) , E ( G ) , Φ G > <V(G),E(G),\Phi_G> <V(G),E(G),ΦG>
- V(G)是一个非空的结点集合
- E(G)是边的集合
- 关联函数 Φ G \Phi_G ΦG :是从边集E与结点偶对间的映射函数
4.1.2 图的分类
按边类型分类
有向图:每一条边都是有向边
- 有向边(弧):边对应的偶对是有序的,用序偶对
<
a
,
b
>
<a,b>
<a,b> 表示
- 有向边的端点:弧的始点与终点
无向图:图中的每一条边都是无向的
- 无向边(棱):偶对无序,用偶对 ( a , b ) (a,b) (a,b) 表示
混合图:图中一些边是有向边,一些边是无向边
- 混合边:两结点间既有有向边,又有无向边,用 [ a , b ] [a,b] [a,b] 表示
结点间的边数
平行边
- 有向图:两结点间(包括结点自身间),若同始点和终点的边多于一条,则这几条边称为平行边
- 无向图:两结点间(包括结点自身间),若多于一条边,则称这几条边为平行边
重数:两结点间互相平行的边的条数称为 [a,b] 的重数。注意有向图需要同始点同终点
多重图:含有平行边的图
线图:不含平行边的图
- 简单图:无自回路的线图
- 平凡图仅有一个结点的简单图
特殊的图
-
零图:全由孤立结点构成的图
孤立结点:不与任何结点邻接的结点
-
含有自回路的图
自回路:关联于同一结点的一条边
-
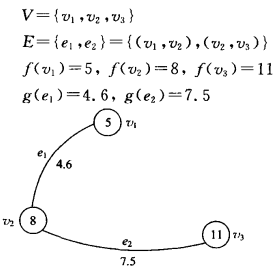
赋权图:边或结点上带有信息,用 三重组或者四重组 表示 < V , E , g > 或 < V , E , f , g > <V,E,g>或<V,E,f,g> <V,E,g>或<V,E,f,g>
- V:结点集合
- E:边的集合
- f:定义在边上的函数
- g:定义在结点上的函数
如:
4.1.3 邻接关系
点的邻接:两结点间由边
边邻接:几条边关联于同一结点,则边邻接
4.1.4 有向图的底图
把有向图总的每条边都看做无向边,得到无向图,称为底图
4.1.5 结点的次数(度)
-
出度(引出次数):有向图中,以结点v为始点的边的条数,记为 d e g + ( v ) deg^+(v) deg+(v)
-
入度(引入次数):有向图中,以结点v为终点的边的条数,记为 d e g − ( v ) deg^-(v) deg−(v)
-
次数(度数):结点v的引出次数和引入次数之和称为结点v的条数,记为 d e g ( v ) deg(v) deg(v)
- 孤立结点v的次数为零
定理
(n,m)图 :n个结点m条边
握手定理:设G是一个(n,m)图,结点集合为 { v 1 , v 2 , . . . , v n } \{v_1,v_2,...,v_n\} {v1,v2,...,vn} ,则
- 度数之和是边数的二倍: ∑ i = 1 n d e g + ( v i ) + ∑ i = 1 n d e g − ( v i ) = 2 m \sum_{i=1}^n deg^+(v_i)+\sum_{i=1}^n deg^-(v_i)=2m ∑i=1ndeg+(vi)+∑i=1ndeg−(vi)=2m
- 在图中,次数为奇数的结点必为偶数个
正则图:各结点次数均相同的无向图,记为 k-正则图
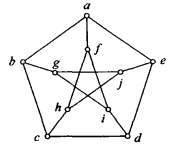
如上图为3-正则图
4.1.6 图间的同构关系
图的同构:设 G = < V , E > G=<V,E> G=<V,E> 和 G ′ = < V ′ , E ′ > G'=<V',E'> G′=<V′,E′> 是两个图,若存在 V到V’ 的双射函数 Φ \Phi Φ ,使对 ∀ a , b ∈ V , [ a , b ] ∈ E \forall a,b\in V,[a,b]\in E ∀a,b∈V,[a,b]∈E 有 [ Φ ( a ) , Φ ( b ) ] ∈ E ′ [\Phi(a),\Phi(b)]\in E' [Φ(a),Φ(b)]∈E′ ,并且 [ a , b ] 与 [ Φ ( a ) , Φ ( b ) ] [a,b]与[\Phi(a),\Phi(b)] [a,b]与[Φ(a),Φ(b)] 有相同的重数
同构的必要条件:
- 结点数相等
- 边数相等
- 度数相同的结点数相等
但不能作为充分条件,如:
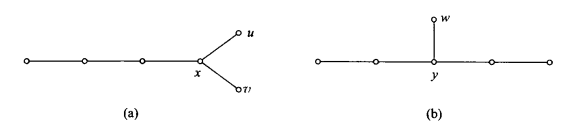
4.1.7 图的运算
设图 G 1 = < V 1 , E 1 > , G 2 = < V 2 , E 2 > , G 2 = < V 3 , E 3 > G_1=<V_1,E_1>,G_2=<V_2,E_2>,G_2=<V_3,E_3> G1=<V1,E1>,G2=<V2,E2>,G2=<V3,E3>
G 1 ∪ G 2 G_1\cup G_2 G1∪G2 : V 3 = V 1 ∪ V 2 , E 3 = E 1 ∪ E 2 V_3=V_1\cup V_2,E_3=E_1\cup E_2 V3=V1∪V2,E3=E1∪E2
G 1 ∩ G 2 G_1\cap G_2 G1∩G2: V 3 = V 1 ∩ V 2 , E 3 = E 1 ∩ E 2 V_3=V_1\cap V_2,E_3=E_1\cap E_2 V3=V1∩V2,E3=E1∩E2
G 1 − G 2 G_1- G_2 G1−G2: E 3 = E 1 − E 2 , V 3 = ( V 1 − V 2 ) ∪ { E 3 中边所关联的顶点 } E_3=E_1- E_2,V_3=(V_1- V_2)\cup \{E_3中边所关联的顶点\} E3=E1−E2,V3=(V1−V2)∪{E3中边所关联的顶点}
G 1 ⊕ G 2 G_1\oplus G_2 G1⊕G2: G 3 = ( G 1 ∪ G 2 ) − ( G 1 ∩ G 2 ) G_3=(G_1\cup G_2)-(G_1\cap G_2) G3=(G1∪G2)−(G1∩G2)
删去图中一个结点v:删去结点v与v关联的所有边
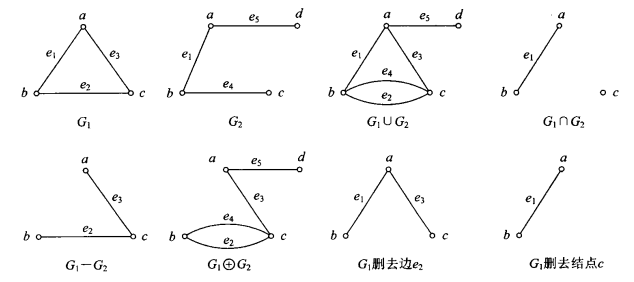
4.1.8 子图
子图
设 G = < V , E > , G ′ = < V ′ , E ′ > G=<V,E>,G'=<V',E'> G=<V,E>,G′=<V′,E′> 是两个图
子图: 如果 V ′ ⊆ V 且 E ′ ⊆ E V'\subseteq V且E'\subseteq E V′⊆V且E′⊆E ,则称G’是G的子图
真子图:如果 G ′ ≠ G G'\neq G G′=G ,则称G’是G的真子图
生成子图: V ′ = V 且 E ′ ⊆ E V'=V且E'\subseteq E V′=V且E′⊆E
由边集E’导出的子图 G [ E ′ ] G[E'] G[E′]:子图G’中没有孤立结点,G’由E’唯一确定
由结点集V’导出的子图 G [ V ′ ] G[V'] G[V′] :子图G’中,对V’中的任意两结点u,v,当 [ u , v ] ∈ E 且 [ u , v ] ∈ E ′ [u,v]\in E且[u,v]\in E' [u,v]∈E且[u,v]∈E′ ,则G’由V’唯一确定
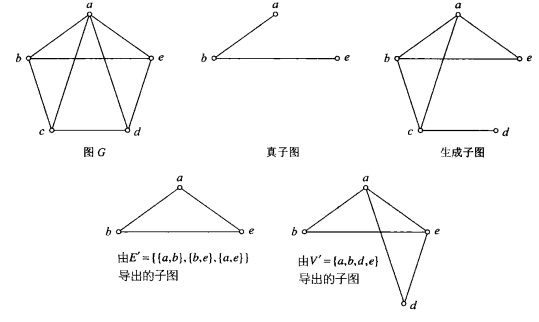
4.1.9 完全图与补图
完全图
- 在n个结点的有向图 G = < V , E > G=<V,E> G=<V,E> 中,如果 E = V × V E=V\times V E=V×V ,则G是有向完全图
- 在n各结点的无向图 G = < V , E > G=<V,E> G=<V,E> 中,如果任何两个不同结点间都有一条边,则称G是无向完全图
补图
设线图 G = < V , E > G=<V,E> G=<V,E> 有n个顶点,线图 H = < V , E ′ > H=<V,E'> H=<V,E′> 也有同样的顶点,而E’是由n个顶点的完全图的边删去E所得,则图H称为G的补图
4.2 图的矩阵表示
设
G
=
<
V
,
E
>
G=<V,E>
G=<V,E> 是一个有向线图。定义一个n阶方阵
A
(
a
i
j
)
A(a_{ij})
A(aij) 为G的邻接矩阵,其中
a
i
j
=
{
1
<
v
i
,
v
j
>
∈
E
0
<
v
i
,
v
j
>
∉
E
a_{ij}=\begin{cases} 1\quad <v_i,v_j>\in E\\ 0\quad <v_i,v_j>\notin E\\ \end{cases}
aij={1<vi,vj>∈E0<vi,vj>∈/E
特殊图的邻接矩阵
零图:零矩阵,元素全为0
每个顶点都有自回路而无其他边:单位矩阵
G的逆图 G ~ \widetilde{G} G :图G的矩阵A的转置矩阵 A T A^T AT
4.2.1 性质
若为有向简单图,则
-
A(G)不一定是对称的
-
对角线为0
-
第i行中值为1的元素数目等于 v i v_i vi 的出度,第j列中值为1的元素数目等于 v j v_j vj 的入度
∑ j = 1 n a i j = d e g + ( v ) ∑ i = 1 n a i j = d e g − ( v ) \sum_{j=1}^na_{ij}=deg^+(v)\quad \sum_{i=1}^na_{ij}=deg^-(v) ∑j=1naij=deg+(v)∑i=1naij=deg−(v)
若G为无向简单图
-
A(G)是对称的
-
对角线为0
-
第i行中值为1的元素数目等于 v i v_i vi 的度,第j列中值为1的元素数目等于 v j v_j vj 的度
∑ j = 1 n a i j = d e g ( v ) ∑ i = 1 n a i j = d e g ( v ) \sum_{j=1}^na_{ij}=deg^(v)\quad \sum_{i=1}^na_{ij}=deg^(v) ∑j=1naij=deg(v)∑i=1naij=deg(v)
4.2.2 矩阵运算的意义
A A T AA^T AAT
令 B = [ b i j ] = A A T B=[b_{ij}]=AA^T B=[bij]=AAT
从结点 v i v_i vi 和 v j v_j vj 两者引出的边,如果能共同终止于一些结点,则这些终止结点的数目就是 v i j v_{ij} vij 的值
对角线上元素的值是各结点的出度
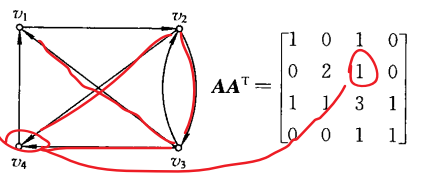
- i=2,j=3, b 23 = 1 b_{23}=1 b23=1 说明从 v 2 v_2 v2 和 v 3 v_3 v3 引出的边能共同终止与同一结点的只有一个
- i=2,j=2, b 22 = 2 b_{22}=2 b22=2,说明 v 2 v_2 v2 的出度为2
A T A A^TA ATA
令 B = [ b i j ] = A T A B=[b_{ij}]=A^TA B=[bij]=ATA
从一些结点引出的边,如果同时终于 v i v_i vi 和 v j v_j vj ,则这些结点的数目为 b i j b_{ij} bij 的值
对角线上元素的值就是结点的入度
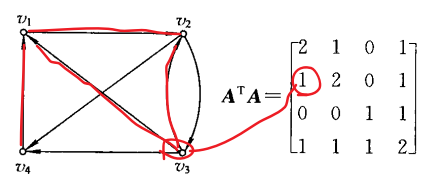
- i=2,j=1, b 21 b_{21} b21 说明以 v 2 v_2 v2 和 v 1 v_1 v1 为终点的边的共同始点只有一个
- i=2,j=2, b 22 b_{22} b22 说明 v 2 v_2 v2 的入度为2
A ( n ) A^{(n)} A(n)
A ( n ) = a i j ( n ) A^{(n)}=a_{ij}^{(n)} A(n)=aij(n) 表示从 v i v_i vi 到 v j v_j vj 的长度为n的不同路径的数目
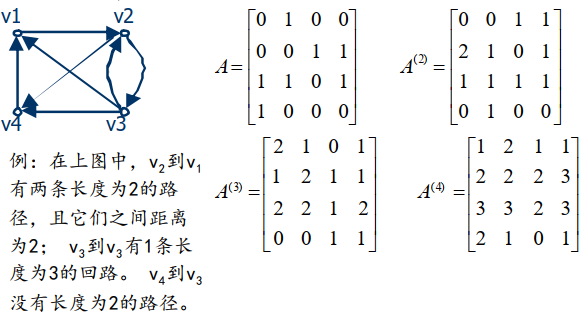
设矩阵 B r = A + A ( 2 ) + . . . + A ( r ) Br=A+A^{(2)}+...+A^{(r)} Br=A+A(2)+...+A(r) , b i j b_{ij} bij 表示从 v i v_i vi 到 v j v_j vj 的长度小于和等于r的不同路径总数
又由于简单有向图中,基本路径长度不超过 n-1,基本回路长度不超过n,则
路径:
B
n
−
1
=
A
+
A
(
2
)
+
.
.
.
+
A
(
n
−
1
)
回路:
B
n
=
A
+
A
(
2
)
+
.
.
.
+
A
n
\begin{aligned} &路径:B_{n-1}=A+A^{(2)}+...+A^{(n-1)}\\ &回路:B_{n}=A+A^{(2)}+...+A^{n} \end{aligned}
路径:Bn−1=A+A(2)+...+A(n−1)回路:Bn=A+A(2)+...+An
b
i
j
b_{ij}
bij 表明了结点间的可达性
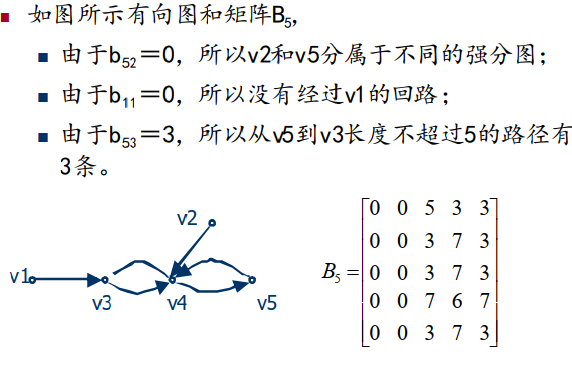
4.3.3 可达矩阵
设 G = < V , E > G=<V,E> G=<V,E> 是一个有向线图, ∣ V ∣ = n \mid V \mid = n ∣V∣=n ,n阶方阵 P i j = ( p i j ) P_{ij}=(p_{ij}) Pij=(pij) ,其中
p
i
j
=
{
1
从
v
i
到
v
j
至少存在一条非零长度的路径
0
从
v
i
到
v
j
不存在一条非零长度的路径
P
=
A
∨
A
(
2
)
∨
.
.
.
∨
A
(
n
)
\begin{aligned} p_{ij}&=\begin{cases} 1\quad从v_i到v_j至少存在一条非零长度的路径\\ 0\quad从v_i到v_j不存在一条非零长度的路径 \end{cases}\\\\ P&=A\vee A^{(2)}\vee ...\vee A^{(n)} \end{aligned}
pijP={1从vi到vj至少存在一条非零长度的路径0从vi到vj不存在一条非零长度的路径=A∨A(2)∨...∨A(n)
则P为可达矩阵
由可达矩阵求强分图
p i j = 1 p_{ij}=1 pij=1 表示从 v i v_i vi 到 v j v_j vj 可达, p j i = p i j T = 1 p_{ji}=p_{ij}^T=1 pji=pijT=1 表示从 v j v_j vj 到 v i v_i vi 可达。仅当 v i v_i vi 与 v j v_j vj 互相可达时,才是连通。
当且仅当 v i v_i vi 和 v j v_j vj 相互可达时, P T ∧ P P^T\wedge P PT∧P 的(i,j) 元素的值为1

4.3 路径与回路
边不重,点不同;简单与基本
从 v 0 到 v n v_0到v_n v0到vn 的路径:图的一个点边交替序列 ( v 0 , e 1 , v 1 , . . . , e n , v n ) (v_0,e_1,v_1,...,e_n,v_n) (v0,e1,v1,...,en,vn) ,
简单路径:同一条边不出现两次的路径
基本路径(链):同一顶点不出现两次
回路:路径始点 v 0 v_0 v0 与 终点 v n v_n vn 重合
简单回路:边不重复的回路
基本回路:通过各顶点的不超过一次的回路
如果是线图,路径P可以用顶点序列表示,称P穿程于顶点序列
路径的长度:路径P所含边的条数。
-
在有n个结点的简单图 G = < V , E > G=<V,E> G=<V,E> 中,如果 v 1 v_1 v1 到 v 2 v_2 v2 有一条路径,则路径长度必不大于 n-1
-
在有n个结点的简单图 G = < V , E > G=<V,E> G=<V,E> 中,如果经 v 1 v_1 v1 有一条简单回路,则经 v 1 v_1 v1 有一条长度不超n的基本回路
4.3.1 连通度与连通图
无向图的连通
在无向图中,连通关系是等价关系,所以可以用连通关系划分无向图
无向图可达
可达:设 G = < V , E > G=<V,E> G=<V,E> 是无向图, v i , v j ∈ V v_i,v_j\in V vi,vj∈V ,如果两点之间存在一条路径,则称 v j 从 v i 可达 v_j从v_i可达 vj从vi可达
无向图连通
连通:在无向图G中,如果任两个结点可达,则称G是连通的
- 连通分图:G的子图G’是连通的,且没有比G’更大的连通图,则G’是G的连通分图
- V上的 等价关系可达 导出的等价类构成的子图
点割
一个无向简单图 G = < V , E > , V ′ ⊂ V G=<V,E>,V'\subset V G=<V,E>,V′⊂V ,如果
(1) ω ( G − V ′ ) > ω ( G ) \omega(G-V') > \omega(G) ω(G−V′)>ω(G) ;删去某些结点后,分图个数大于原图中的分图个数
(2) 不存在 V’的真子集 V’',使得 ω ( G − V ′ ′ ) > ω ( G ) \omega(G-V'')>\omega(G) ω(G−V′′)>ω(G) ;生成分图的是最小删除结点数
,则称V’是图G的点割。
当只删去一个点就形成分图,删除的点称为割点:当 V’={v}时,称 v 为割点
若有生成当前分图有更小的删去点集,则称为泛点割
- 泛点割中包含点割
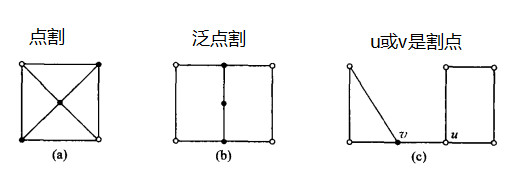
点连通度
G = < V , E > G=<V,E> G=<V,E> 是无向简单连通图。G中含顶点数最小的点割的大小称为G的点连通度。
点连通度 κ 0 ( G ) \kappa_0(G) κ0(G) :使连通图变为不连通图或者平凡图必须删去的顶点数
k-点连通: κ 0 ( G ) ≥ k \kappa_0(G) \ge k κ0(G)≥k ,G至少删去k个点才能变为不连通图
- 完全图 κ 0 ( G ) = n − 1 \kappa_0(G)=n-1 κ0(G)=n−1,平凡图 κ 0 ( G ) = 0 \kappa_0(G)=0 κ0(G)=0
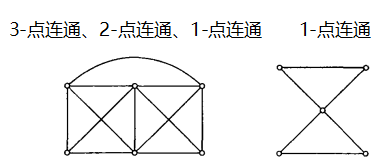
边割集
一个无向简单图 G = < V , E > , E ′ ⊆ E G=<V,E>,E'\subseteq E G=<V,E>,E′⊆E ,如果
(1) ω ( G − E ′ ) > ω ( E ) \omega(G-E') > \omega(E) ω(G−E′)>ω(E) ;删去某些边后,分图个数大于原图中的分图个数
(2) 不存在 E’的真子集 E’',使得 ω ( G − E ′ ′ ) > ω ( E ) \omega(G-E'')>\omega(E) ω(G−E′′)>ω(E) ;生成分图的是最少删除边数
,则称E’是图G的割集。
当只删去一条边就形成分图,删除的点称为割点:当 E’={e}时,称 e 为桥
若有生成当前分图有更小的删去边集,则称为泛割集
- 泛割集中包含割集
连通度
G = < V , E > G=<V,E> G=<V,E> 是无向简单连通图。G中含边数最小的割集的大小称为G的连通度。
连通度 κ 1 ( G ) \kappa_1(G) κ1(G) :使连通图变为不连通图或者平凡图必须删去的边数
k-连通: κ 0 ( G ) ≥ k \kappa_0(G) \ge k κ0(G)≥k ,G至少删去k条边才能变为不连通图
- 平凡图 κ 1 ( G ) = 0 \kappa_1(G)=0 κ1(G)=0
有向图的连通
有向图的可达
可达:设 G = < V , E > G=<V,E> G=<V,E> 是有向图, v i , v j ∈ V v_i,v_j\in V vi,vj∈V ,如果两点之间存在一条路径,则称 v j 从 v i 可达 v_j从v_i可达 vj从vi可达
连通分类
强连通:任两个结点偶对中,两结点互相可达,则称G是强连通的
- 所有顶点都在一条回路上
单向连通:任两个结点偶对中,至少从一个结点到另一个结点是可达的
- 存在一条有向路径,穿程于图的全部结点
弱连通:一个有向图的底图是连通的,则G是弱连通的
分图
强分图:在有向图 G = < V , E > G=<V,E> G=<V,E> 中,G’是G的子图,G’是强连通的,没有比G’更大的强连通图
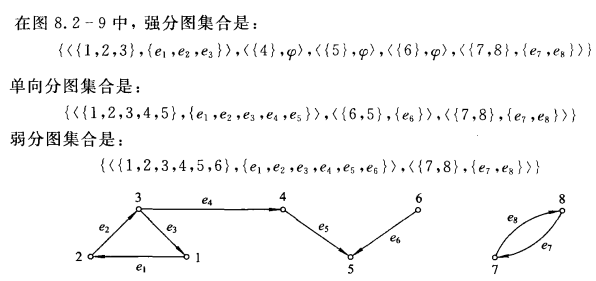
“在同一强分图中”,“在同一弱分图中”,是图的顶点集V上的等价关系,这个等价关系把V划分成若干个等价类,即分图
强连通关系是等价关系,所以可以通过强连通关系划分为强
应用
死锁的检测
- 分配图:结点表示资源,边的始点表示占有,终点表示请求
- 用矩阵方法能够识别包含多于一个结点的强分图,从而检测出死锁状态
4.3.2 最短路径
结点间的距离 d ( v i , v j ) d(v_i,v_j) d(vi,vj) :在图 G = < V , E > G=<V,E> G=<V,E> 中,从结点 v 1 v_1 v1 到 v j v_j vj 最短路径的长度
-
有向图中, d ( v i , v j ) d(v_i,v_j) d(vi,vj) 不一定等于 d ( v j , v i ) d(v_j,v_i) d(vj,vi) ,但满足三角等式
d ( v i , v j ) ≥ 0 d(v_i,v_j)\ge 0 d(vi,vj)≥0
d ( v i , v i ) = 0 d(v_i,v_i)=0 d(vi,vi)=0
d ( v i , v j ) + d ( v j , v k ) ≥ d ( v i , v k ) d(v_i,v_j)+d(v_j,v_k) \ge d(v_i,v_k) d(vi,vj)+d(vj,vk)≥d(vi,vk)
带权图单源点最短路径
设 G = < V , E , W > G=<V,E,W> G=<V,E,W> 是个带权图,W是从E到正实数集合的函数
路径P的长度定义为路径中边的长度之和,记为W§
d
(
u
,
v
)
=
{
m
i
n
{
W
(
P
)
∣
P
为
G
中从
u
到
v
的路径
}
∞
当从
u
到
v
不可达
d(u,v)= \begin{cases} min\{W(P)|P为G中从u到v的路径\}\\ \infty 当从u到v不可达 \end{cases}
d(u,v)={min{W(P)∣P为G中从u到v的路径}∞当从u到v不可达
Dijkstra算法(贪心)
单源点多汇点
(1)将V分成两个子集S,有源点a的集合S与没有源点a的集合T。各结点到源点a的距离向量D(x)是他们之间的直接距离W(a,x)
(2)根据D(x)从集合T中找出与源点距离最短的结点t,以t为中转更新T中剩余结点到a点的距离向量D(x);
- D(x)=min[D(x),D(t)+W(t,x)];原先点a到点x的距离 与 到点t的距离+t与x之间的距离 的最小值
(3)将t并于S,T=T-{t}。若T=∅,则结束,反之执行(2)

Floyd(动态规划)
适用场景:无负权回路求 多源点多汇点间的最短路径
原理
-
在一个图中,最短路径长度不会超过 n-1
-
任意节点i与j的最短路径只有两种可能:
(1) [i,j] 本身最短
(2) 从i经过若干节点到j
故其状态转移方程为
path[i,j]=min{path[i,k]+path[k,j],path[i,j]}
步骤
-
初始状态:
矩阵A:记录各结点间的直接距离
矩阵P:A中不为无穷的点置1
路径计数器k=-1,
A ( k ) [ i ] [ j ] A^{(k)}[i][j] A(k)[i][j] 记录的是经过前k个顶点的最短路径
P ( k ) [ i ] [ j ] P^{(k)}[i][j] P(k)[i][j] 记录经过前k个顶点的最短路径长度
-
k++
判断在已加入前k-1个结点基础上再加上 v k − 1 v_{k-1} vk−1 中转是否使路径变短(除去第k行和第k列和主对角线上的元素,A矩阵中其余元素计算 m i n { A ( k − 1 ) [ i ] [ j ] , A ( k ) [ i ] [ j ] } min\{A^{(k-1)}[i][j],A^{(k)}[i][j]\} min{A(k−1)[i][j],A(k)[i][j]})。
如果取 A ( k ) [ i ] [ j ] A^{(k)}[i][j] A(k)[i][j] ,则相应的令 A ( k ) [ i ] [ j ] = A ( k ) [ i ] [ j ] , P ( k ) = P ( k − 1 ) [ i ] [ j ] + 1 A^{(k)}[i][j]=A^{(k)}[i][j],P^{(k)}=P^{(k-1)}[i][j]+1 A(k)[i][j]=A(k)[i][j],P(k)=P(k−1)[i][j]+1 ,
否则令 A ( k ) [ i ] [ j ] = A ( k − 1 ) [ i ] [ j ] , P ( k ) = P ( k − 1 ) [ i ] [ j ] A^{(k)}[i][j]=A^{(k-1)}[i][j],P^{(k)}=P^{(k-1)}[i][j] A(k)[i][j]=A(k−1)[i][j],P(k)=P(k−1)[i][j]
-
若k=n-1,停止;否则继续第二步
4.3.3 关键路径(动态规划)
单源点到单汇点的最长路径
从源点到汇点,算最长路径有多长
从汇点到源点,哪条路径是最长路径
-
输入e 条弧 ,建立AOE-网存储结构
-
拓扑排序,求得事件的最早开始时间,最后得到活动的最晚结束时间。从源点出发,源点的最早开始时间
ve[0]=0,按拓扑有序求其余各顶点的最早开始时间ve[i]。如果得到的拓扑序列顶点数小于AOE网中的顶点数,则说明网中有环,无关键路径。- 拓扑排序:入度为0的点,若取出该点,删除以该点为始点的边
- 最早开始时间
ve[i]为源点到顶点i的最长距离
-
逆拓扑排序,求得顶点的最晚开始时间。从汇点出发,令汇点的最晚开始时间等于最早开始时间
vl[n-1]=ve[n-1],依次求得各事件的最晚开始时间vl[i]- 逆拓扑排序:出度为0的点,若取出该点,删除以该点为终点的边
- 最晚开始时间
vl[i]为顶点i的所有出边终点的最晚开始时间减去边的权值的最小值
-
根据个顶点的 最早开始时间
ve[i]和最晚开始时间vl[i],求每个边的最早开始时间e[i]和最晚开始时间l[i],满足最早开始时间=最晚开始时间的边为关键路径活动的最早开始时间=活动始点事件的最早开始时间
活动的最晚开始时间=活动终点事件的最晚开始时间-活动时间
4.3.4 欧拉路径与欧拉回路
欧拉:拉——边;哈密尔顿:口多——结点○
无向连通图G
欧拉路径:穿程于图G的每条 边 一次且仅一次的 路径
欧拉回路:穿程于图G的每条 边 一次且仅一次的 回路
欧拉图:具有欧拉回路的图
充要条件
无向连通图
具有欧拉路径:当且仅当G中具有零个或两个奇数度的顶点
欧拉图:当且仅当该图的顶点次数都是偶数
有向连通图
具有欧拉路径:
- 每个顶点出度等于入度
- 路径起点:出度-入度=1,路径终点:入度-出度=1
具有欧拉回路:当且仅当每个顶点的出度等于入度
4.3.5 哈密尔顿图
哈密尔顿路径:在无向图 G = < V , E > G=<V,E> G=<V,E> 中穿程与G的每个结点一次且仅一次的路径
哈密尔顿回路:穿程于G的每个结点一次且仅一次的回路
哈密尔顿图:含有哈密尔顿回路的图
必要条件
删去的结点数大于等于删去结点后生成的分图数
设 G = < V , E > G=<V,E> G=<V,E> 是哈密尔顿图,对V的每个非空真子集S,有 ω ( G − S ) ≤ ∣ S ∣ \omega(G-S)\le \mid S \mid ω(G−S)≤∣S∣ , ω ( G − S ) \omega(G-S) ω(G−S) 表示删去S后形成的连通分图个数

充分条件
设 G = < V , E > G=<V,E> G=<V,E> 是具有 n ≥ 3 n\ge 3 n≥3 个顶点的简单无向图,
-
若在G中每一对顶点的度数之和大于等于n-1
-
每一个 顶点的度数大于等于 n 2 \frac{n}{2} 2n
则在G中存在一条哈密尔顿回路
4.4 二部图和平面图
4.4.1 二部图
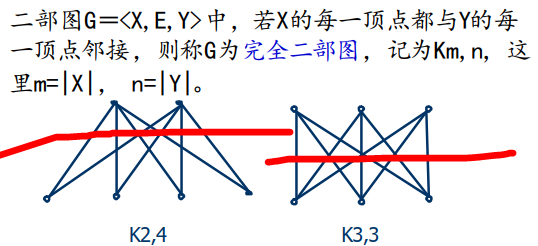
若无向图 G = < V , E > G=<V,E> G=<V,E> 的结点集合V可以划分为两个子集 X和Y ,使G中每一条边e,其一个端点在X中,另一个端点在Y中,则称 G是二部图或偶图
记为 G = < X , E , Y > G=<X,E,Y> G=<X,E,Y> ,X和Y称为 互补结点子集。
- 二部图没有自回路
完全二部图:若 X的每一顶点都与Y的每一顶点邻接,则称G为完全二部图
充要条件
无向图G中的所有回路长度均为偶数
4.4.2 平面图
相关概念
设 G = < V , E > G=<V,E> G=<V,E> 是一个无向图,如果能把G的所有结点和边画在一个平面上,且使得任何两条边除了端点外没有其他交点,则G是一个平面图

面:设G施一个连通平面图,由图中的边所包围的区域,在区域内既不包含图的结点,也不包含图的边,这样的区域为图的一个面
边界:包围面的边构成的回路
面的次数:面的边界回路的长度,记为deg®

一个有限平面图,面的次数之和边数的两倍
充要条件
欧拉公式:一个连通的平面图G,共有n个结点,m条边和k个面,则欧拉公式 n-m+k=2成立
顶点数-边数+面数=2
推论:
-
一个连通简单平面图,共n个结点,m条边,若 n ≥ 3 n\ge 3 n≥3,则 m ≤ 3 n − 6 m\le 3n-6 m≤3n−6
-
一个连通简单平面图,共n个结点,m条边,若每个平面至少四条边组成,则 m ≤ 2 n − 4 m\le 2n-4 m≤2n−4
-
一个连通简单平面图,共n个结点,m条边,若每个平面至少s( s ≥ 3 s\ge 3 s≥3)条边组成,则 m ≤ s ( n − 2 ) s − 2 m\le \frac{s(n-2)}{s-2} m≤s−2s(n−2)
库拉托夫斯基定理
在给定图G的边上,
插入一个新的度为2的结点,使一条边分成两条边
关联于一个度为2的结点的两条边,去掉这个结点,使两条边化为一条边
不会影响图的平面性
对偶图
给定平面图 G = < V , E > G=<V,E> G=<V,E> ,将其嵌入平面后:
- 在图G的每一个面 D i D_i Di 内部作一个且仅做一个结点 v i ∗ v_i^* vi∗
- 经过每两个面 D i D_i Di 与 D j D_j Dj 的每一边界 e k e_k ek 做一条边 e k ∗ e_k^* ek∗ ,使 e k ∗ = ( v i ∗ , v j ∗ ) e_k^*=(v_i^*,v_j^*) ek∗=(vi∗,vj∗) 与 e k e_k ek 相交
- 当且仅当 e k e_k ek 只是一个面 D i D_i Di 的边界时, v i ∗ v_i^* vi∗ 恰好存在一个自回路 e k ∗ e_k* ek∗ 与 e k e_k ek 相交
则称G*是G的一个对偶图
4.5 无向树
连通且无简单回路的无向图称为无向树
树中次数为1的结点称为树叶,次数大于1的结点称为分支点或内部结点
- 任何一棵树至少有两片树叶( n ≥ 2 n\ge 2 n≥2)
一个无向图的各连通分图大都是树时,该无向图称为森林
4.5.1 树的等价定义
- 无简单回路的连通图
- 无简单回路,且边数=结点数-1
- 连通且边数=结点数-1
- 无简单回路,但增加一条新边得到且仅得到一条基本回路
- 连通,但删去一条边后不连通
- 每一对结点之间有且仅有一条基本路径
4.5.2 生成树
相关概念
在无向图G的一个生成子图T是一棵树,则T为G的生成树或支撑树
生成树T中的边称为树枝,图G中不在生成树中的边称为弦,所有的弦的集合称为生成树T的补
-
任何连通无向图至少有一棵生成树
-
无向连通图G有n个结点,m条边,G的生成树有 n-1条边。则要删除m-n+1条边。
连通图G的秩:m-n+1
-
一个连通图可以生成许多树。确定一个回路后,可删除回路中不同的边,进而生成不同的树
-
一条简单回路和任何一棵生成树的补至少有一条公共边
简单回路至少去掉一条边后才不构成回路
-
一个割集和任何生成树至少有一条公共边
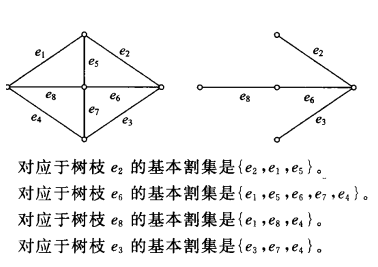
基本割集
生成树T中删去一条枝,将顶点集划分为两个子集(生成两个分图)。从G变为当前分图的边割集称为该枝对应的基本割集
4.5.3 最小生成树
设 G = < V , E , W > G=<V,E,W> G=<V,E,W> 是连通简单无向带权图。
W(T):T的生成树的树权
最小生成树:在G的所有生成树中,树权最小的生成树称为最小生成树
Kruskal(选边)
图中有n个结点
(1) 将边集划分为两个集合,T和E-T,边计数器 i=0
(2) 选择E-T中边权最小的边 $ e_k$ ,若加入 e k e_k ek 后不会使T形成回路,则选择 e k e_k ek 放入T, E − T − { e k } E-T-\{e_k\} E−T−{ek} ,i++;
(3) 若 i < n-1,则执行(2);T即为最小生成树
Prime(选点)
图中有n个结点
(1) 将结点集分为两个集合,T 和 V-T,并选定一个点加入S,点计数器i=1
(2) 在边集E中,找一条最小代价边,他的一个端点在T,另一个端在V-T中。
将该边不在T集的端点加入T集,V-T-{p},i++
(3) 若i < n,执行第二步。
4.6 有向树
有向树定义:
有且仅有一个结点叫树根
除树根外,每一结点的入度都是1
树的每一个结点a,都有从树根到a的一条有向路径
4.6.1 相关概念
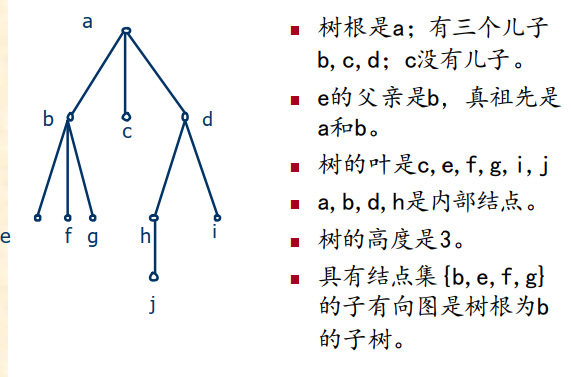
有序树:树中每一结点引出的边都规定次序的树,称为有序树
位置树:如果树中的每一结点的儿子不仅给出次序,还明确他们的位置,称为位置树。二叉树是位置树
有向森林:每个连通分图是有向树
有序森林:所有树都是有序树,且给树指定了次序
4.6.2 性质
-
设T是一棵有向树,根是r,并设a是T的任一结点,则从r到a有唯一的有向路径
-
有向树中的每一有向路径是基本路径
-
有向树没有非零长度的任何回路
-
有向树中,结点树=边数+1
-
有向树的子树是有向树
-
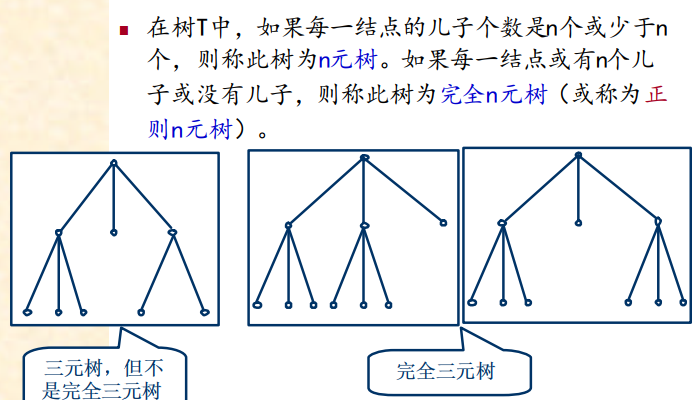
完全n元树,树叶与分支结点数的关系

4.6.3 带权二元树
给定一组权 w 1 , w 2 , . . . , w t w_1,w_2,...,w_t w1,w2,...,wt ,设有一颗完全二元树有t片叶子,每个叶子上带有一个权值,则称该二元树为带权二元树、
带权路径长度:带权二元树中,带权为 w i w_i wi 的树叶,其通路长度为 L ( w i ) L(w_i) L(wi) ,将 W ( T ) = ∑ i = 1 t w i ⋅ L ( w i ) W(T)=\sum_{i=1}^{t} w_i·L(w_i) W(T)=∑i=1twi⋅L(wi) ,称为带权二元树的权。
在所有带权的二元树中,带权路径长度最小的那棵树称为最优树
性质
设T为带权 w 1 ≤ w 2 ≤ … ≤ w t w_1≤ w_2≤ … ≤ w_t w1≤w2≤…≤wt 的最优树, 则
- 带权 w 1 , w 2 w_1,w_2 w1,w2 的树叶 v w 1 , v w 2 v_{w_1},v_{w_2} vw1,vw2 是兄弟;
- 以树叶 v w 1 , v w 2 v_{w_1},v_{w_2} vw1,vw2 为儿子的分枝点,是通路长度最长( 层次最大) 的分枝点
哈夫曼编码
给定一个序列集合,若没有一个序列是另一个序列的前缀,则将该序列集合称为前缀码
任何一棵二元树的树叶可对应一个前缀码
任何一个前缀码都对应一棵二元树