一、题目
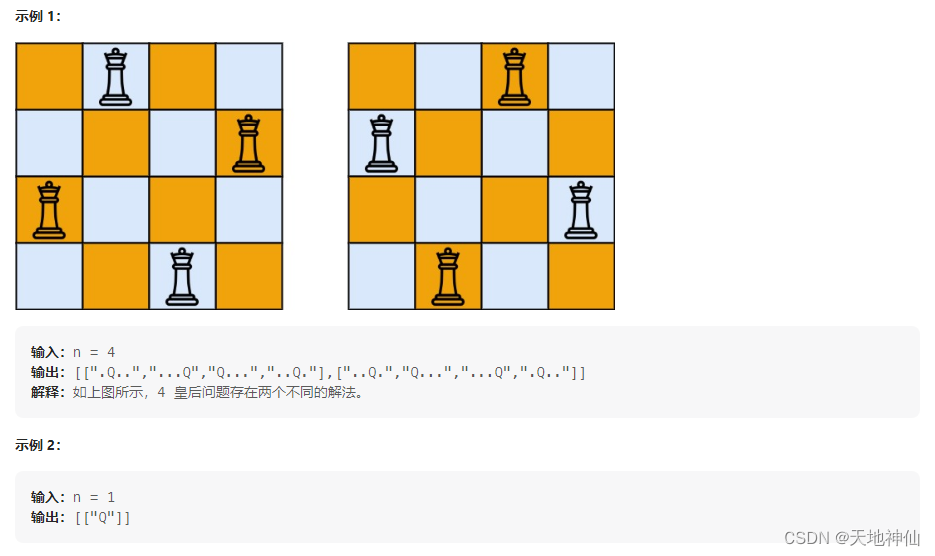
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/n-queens/description/
二、C++解法
我的思路及代码
采用回溯的思想。这里需要一个判断的函数 isValid ,来处理当前位置是否是可选的位置。每一次选择的时候都会前进一行,然后在当前行中,选择可用的列。如果这个列是可用的那么就可以选择此路径,然后继续后面的回溯,如果不可用则继续往下找。本质是一个全排列的问题。由于我们的方式是从一行一行的往下找,那么在 isValid 中,就不必判定左下角和右下角的合理情况,这必然是可选的。
class Solution {
public:
vector<vector<string>> ans;
bool isValid(int &row,int &col,vector<string> &temp){
int rowTemp = row;
int colTemp = col;
//判断列有没有棋子
for(int i=0;i<temp.size();i++){
if(temp[i][col] == 'Q')
return false;
}
//判断左上有没有棋子
for(;rowTemp>=0&&colTemp>=0;rowTemp--,colTemp--){
if(temp[rowTemp][colTemp] == 'Q')
return false;
}
//判断右上有没有棋子
for(rowTemp = row,colTemp = col;rowTemp>=0&&colTemp<temp.size();rowTemp--,colTemp++){
if(temp[rowTemp][colTemp] == 'Q')
return false;
}
return true;
}
void backtrance(vector<string> &temp,int row){
if(row==temp.size()){
ans.push_back(temp);
return;
}
for(int col=0;col<temp.size();col++){
if(isValid(row,col,temp)){
temp[row][col] = 'Q';
backtrance(temp,row+1);
temp[row][col] = '.';
}
}
}
vector<vector<string>> solveNQueens(int n) {
vector<string> temp(n,string(n,'.'));
backtrance(temp,0);
return ans;
}
};
- 时间复杂度:O(N!),其中 N 是皇后数量
- 空间复杂度:O(N),其中 N 是皇后数量。空间复杂度主要取决于递归调用层数、记录每行放置的皇后的列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N
官方参考代码
方法一:基于集合的回溯
采用了集合的方式来存储各个线上皇后的情况,本质还是回溯算法。
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
auto solutions = vector<vector<string>>();
auto queens = vector<int>(n, -1);
auto columns = unordered_set<int>();
auto diagonals1 = unordered_set<int>();
auto diagonals2 = unordered_set<int>();
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
void backtrack(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {
if (row == n) {
vector<string> board = generateBoard(queens, n);
solutions.push_back(board);
} else {
for (int i = 0; i < n; i++) {
if (columns.find(i) != columns.end()) {
continue;
}
int diagonal1 = row - i;
if (diagonals1.find(diagonal1) != diagonals1.end()) {
continue;
}
int diagonal2 = row + i;
if (diagonals2.find(diagonal2) != diagonals2.end()) {
continue;
}
queens[row] = i;
columns.insert(i);
diagonals1.insert(diagonal1);
diagonals2.insert(diagonal2);
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
queens[row] = -1;
columns.erase(i);
diagonals1.erase(diagonal1);
diagonals2.erase(diagonal2);
}
}
}
vector<string> generateBoard(vector<int> &queens, int n) {
auto board = vector<string>();
for (int i = 0; i < n; i++) {
string row = string(n, '.');
row[queens[i]] = 'Q';
board.push_back(row);
}
return board;
}
};
- 时间复杂度:O(N!),其中 N 是皇后数量
- 空间复杂度:O(N),其中 N 是皇后数量。空间复杂度主要取决于递归调用层数、记录每行放置的皇后的列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N