看见统计——第三章 概率分布
参考
- https://github.com/seeingtheory/Seeing-Theory
- 中心极限定理
概率分布描述了随机变量取值的规律。
随机变量Random Variables
🔥 定义:将样本空间中的结果映射到实数的函数
X
X
X 称为随机变量(random variable),记为
X
:
Ω
→
X:\Omega\to
X:Ω→
例如,在抛硬币问题中,样本空间就是 Ω = 正面,背面 \Omega={正面,背面} Ω=正面,背面,随机变量有 X ( 正面 ) = 1 , X ( 背面 ) = 0 X(正面)=1,X(背面)=0 X(正面)=1,X(背面)=0。
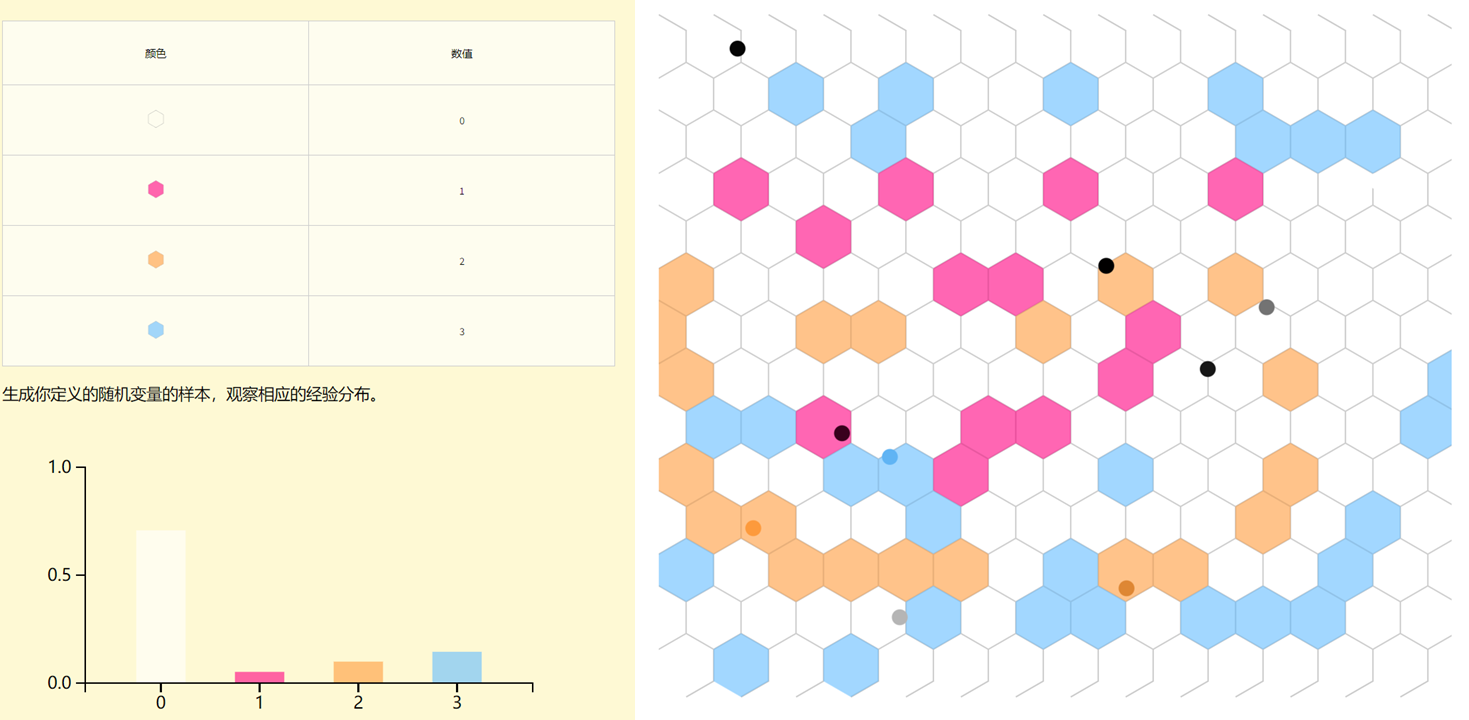
随机变量是一个函数,它用数字来表示一个可能出现的事件。你可以定义你自己的随机变量,然后生成一些样本来观察它的经验分布。
随机变量的独立性
🔥 定义:假设
X
X
X和
Y
Y
Y是定义在某个样本空间
Ω
Ω
Ω上的两个随机变量。对于任意的两个子集
A
A
A 和
B
B
B ,当满足:
P
(
X
∈
A
,
Y
∈
B
)
=
P
(
X
∈
A
)
P
(
Y
∈
B
)
P(X\in A,Y\in B)=P(X\in A)P(Y\in B)
P(X∈A,Y∈B)=P(X∈A)P(Y∈B)
时,我们说
X
X
X 和
Y
Y
Y 是独立的随机变量
再来证明:如果 X X X 和 Y Y Y 是独立的随机变量,那么 E [ X Y ] = E [ X ] E [ Y ] E[XY]=E[X]E[Y] E[XY]=E[X]E[Y]。定义随机变量 Z ( ω ) = X ( ω ) Y ( ω ) Z(\omega)=X(\omega)Y(\omega) Z(ω)=X(ω)Y(ω),根据期望的定义,左式可以写成:
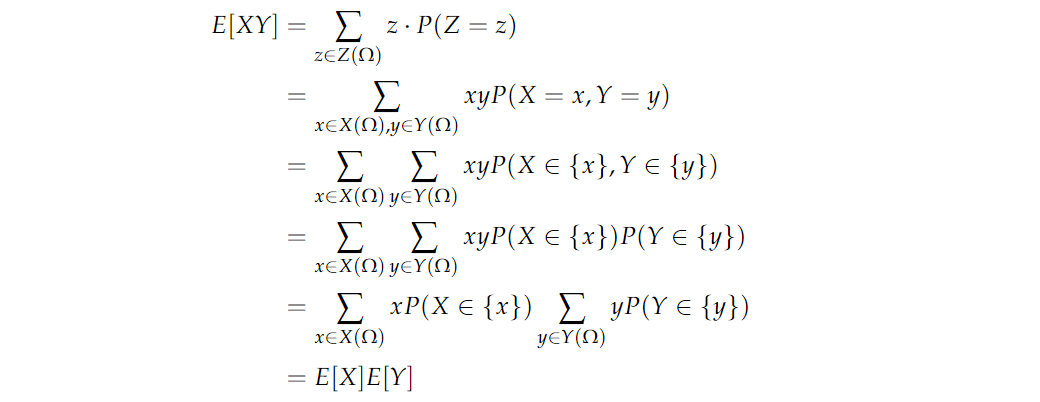
离散型和连续型随机变量Discrete and Continuous
常见的随机变量类型有两种:离散型随机变量和连续型随机变量。
离散型随机变量
一个离散型随机变量可能的取值范围只有有限个或可列个值。离散型随机变量的定义是:如果
X
X
X 是一个随机变量,存在非负函数
f
(
x
)
f(x)
f(x) 和
F
(
x
)
F(x)
F(x),使得:
P
(
X
=
x
)
=
f
(
x
)
P
(
X
<
x
)
=
F
(
x
)
P(X=x) = f(x) \\ P(X < x) = F(x)
P(X=x)=f(x)P(X<x)=F(x)
则称
X
X
X 是一个离散型随机变量。
分布函数 F ( x ) F(x) F(x):Cumulative Distribution Function, 简称CDF。
概率质量函数 f ( x ) f(x) f(x):probability mass function,简写为PMF。是离散随机变量在各特定取值上的概率。
图示中黄色曲线为PMF,橙色曲线为CDF。
例如,我们的掷硬币产生了一个随机变量 X X X ,它只能接受集合 { 0 , 1 } \{0,1\} {0,1}中的值。因此, X X X 是一个离散的随机变量。然而,离散随机变量仍然可以具有无穷多个值,如下所示。
泊松分布Poisson
泊松分布表示了一个事件在固定时间或者空间中发生的次数。泊松分布的参数 λ λ λ 是单位时间(或单位面积)内随机事件的平均发生次数。比方说,我们可以用泊松分布来刻画流星雨或者足球比赛中的进球数。
在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率 λ λ λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布 $P(\lambda) $。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位。(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性。)
设随机变量
X
X
X 服从参数为
λ
λ
λ(
k
∈
N
k\in\N
k∈N) 的泊松分布,即
P
(
X
=
k
)
=
λ
x
e
−
λ
k
!
P(X=k) =\dfrac{\lambda^{x}e^{-\lambda}}{k!}
P(X=k)=k!λxe−λ
描述这种分布的简写是
X
∼
P
o
i
(
λ
)
X∼Poi(λ)
X∼Poi(λ)。因为
k
k
k 可以是
N
\N
N 中的任何数字,所以我们的随机变量
X
X
X 在无穷多个数字上具有正的概率。然而,由于
N
N
N 是可数的,
X
X
X 仍然被认为是离散型随机变量。
| PMF | 期望 | 方差 |
|---|---|---|
| f ( x ; λ ) = λ x e − λ x ! f(x;\lambda) = \dfrac{\lambda^{x}e^{-\lambda}}{x!} f(x;λ)=x!λxe−λ | λ \lambda λ | λ \lambda λ |
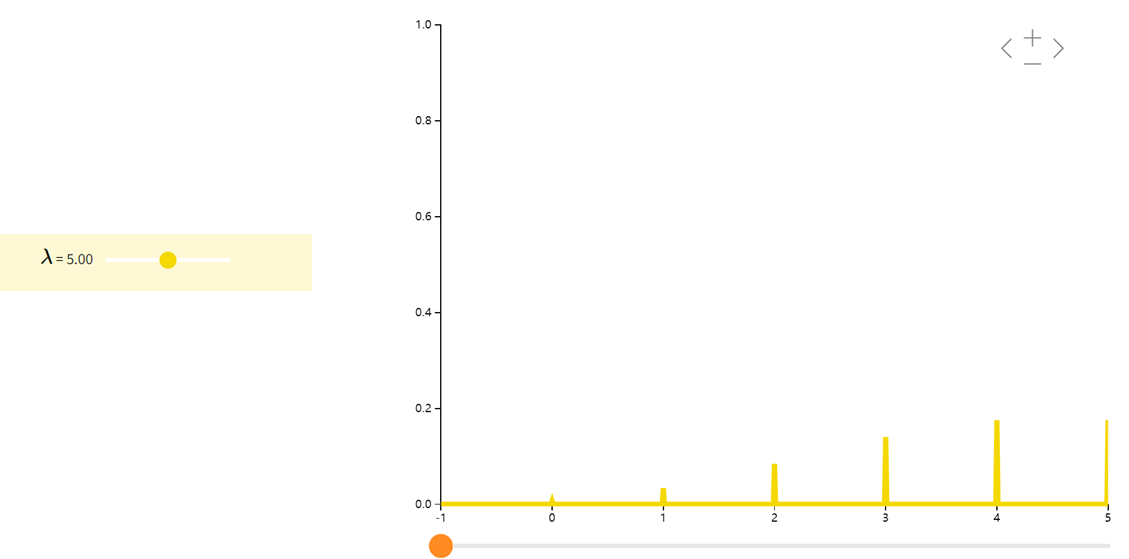
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当 n ≥ 20 , p ≤ 0.05 n\ge20,p\le0.05 n≥20,p≤0.05 时,就可以用泊松公式近似得计算。
伯努利分布Bernoulli
如果一个随机变量
X
X
X 只取值 0 或 1,概率分布是
P
(
X
=
1
)
=
p
,
P
(
X
=
0
)
=
1
−
p
P(X=1)=p,\quad P(X=0)=1-p
P(X=1)=p,P(X=0)=1−p
则称
X
X
X 符合伯努利分布(Bernoulli)。我们常用伯努利分布来模拟只有两种结果的试验,如抛硬币。
| PMF | 期望 | 方差 |
|---|---|---|
| f ( x ; p ) = { p if x = 1 1 − p if x = 0 f(x;p) = \begin{cases} p & \text{if } x = 1 \\ 1-p & \text{if } x = 0 \end{cases} f(x;p)={p1−pif x=1if x=0 | p p p | p ( 1 − p ) p(1-p) p(1−p) |
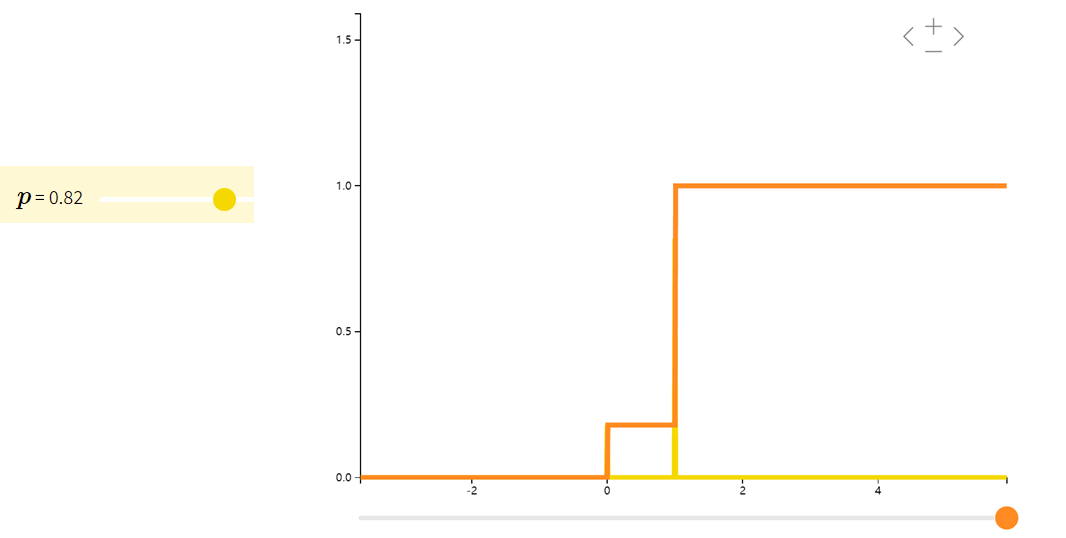
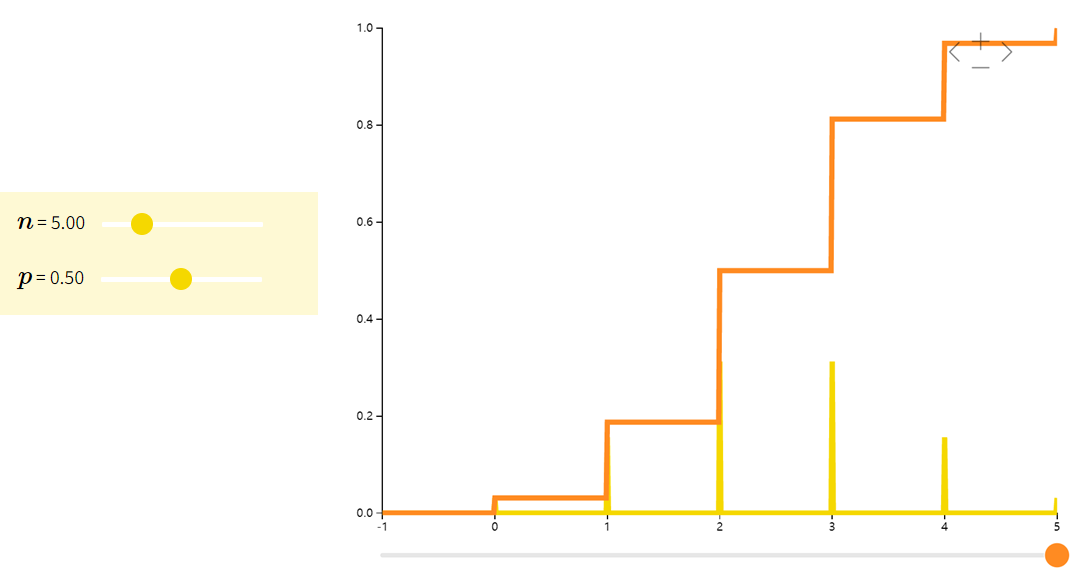
二项分布Binomial
如果随机变量
X
X
X 是
n
n
n 个参数为
p
p
p 的独立伯努利随机变量之和,则称
X
X
X 是二项分布(binomial)。我们常用二项分布来模拟若干独立同分布的伯努利试验中的成功次数。比如说,抛五次硬币,其中正面的次数可以用二项分布来表示:
B
i
n
(
5
,
1
/
2
)
Bin(5,1/2)
Bin(5,1/2)。
| PMF | 期望 | 方差 |
|---|---|---|
| f ( x ; n , p ) = ( n x ) p x ( 1 − p ) n − x f(x; n,p) = \binom{n}{x}p^{x}(1-p)^{n-x} f(x;n,p)=(xn)px(1−p)n−x | n p np np | n p ( 1 − p ) np(1-p) np(1−p) |
例如。 P ( X = 2 ) = C 5 2 ( 1 2 ) 5 = 10 32 = 0.3125 P(X=2)=C_5^2(\frac{1}{2})^5=\frac{10}{32}=0.3125 P(X=2)=C52(21)5=3210=0.3125
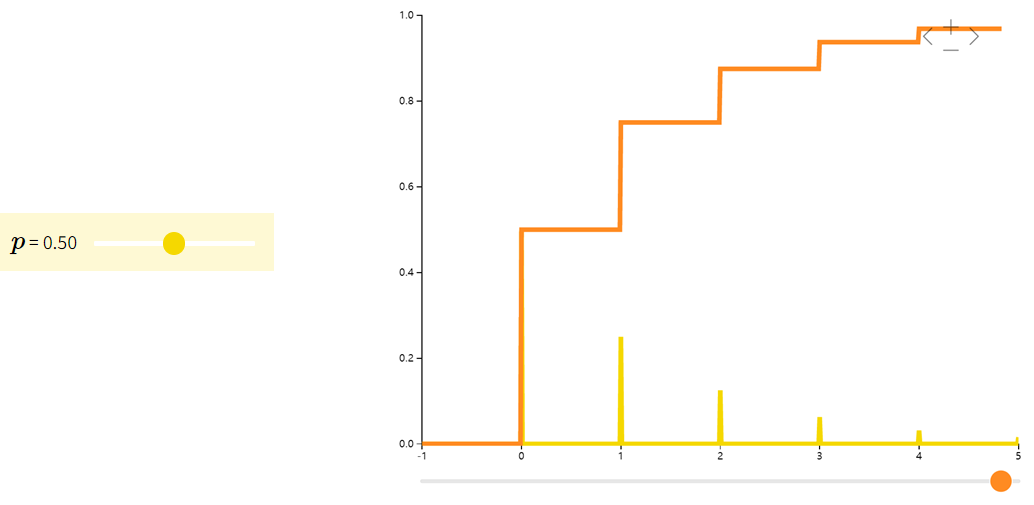
几何分布Geometric
定义:指在伯努利试验中,试验r次才得到第一次成功的机率。即前r-1次都失败,在第r次成功的概率。
示例:射箭第几次能够正中靶心、有放回的情况下第几次能取到期望颜色的小球等等,求这种多次进行的试验下第几次能够达到想要的目的。
| PMF | 期望 | 方差 |
|---|---|---|
| f ( x ; p ) = ( 1 − p ) x p f(x; p) = (1-p)^{x}p f(x;p)=(1−p)xp | 1 p \frac{1}{p} p1 | 1 − p p 2 \frac{1-p}{p^2} p21−p |
连续型随机变量
连续型随机变量可能取值的范围是一个无限不可数集合(如全体实数)。连续型随机变量的定义是:设
X
X
X 为随机变量,存在非负函数
f
(
x
)
f(x)
f(x) 使得:
P
(
a
≤
X
≤
b
)
=
∫
a
b
f
(
x
)
d
x
P
(
X
<
x
)
=
F
(
x
)
P(a\leq X\leq b) =\int^b_a f(x) dx \\P(X< x) = F(x)
P(a≤X≤b)=∫abf(x)dxP(X<x)=F(x)
概率密度函数
f
(
x
)
f(x)
f(x): probability density function,PDF,是一个描述这个连续型随机变量的输出值,在某个确定的取值点附近的可能性的函数。概率密度函数如果满足以下两个性质则有效:
- ∀ x ∈ Ω , f ( x ) ≥ 0 \forall x\in\Omega,f(x)\ge 0 ∀x∈Ω,f(x)≥0
- ∫ − ∞ ∞ f ( x ) d x = 1 \int^{∞}_{-∞}f(x)dx=1 ∫−∞∞f(x)dx=1
均匀分布Uniform
如果随机变量
X
X
X 在其支撑集上所有相同长度的区间上有相同的概率。即如果
b
1
−
a
1
=
b
2
−
a
2
b_1-a_1 = b_2-a_2
b1−a1=b2−a2 则有
P
(
X
∈
[
a
1
,
b
1
]
)
=
P
(
X
∈
[
a
2
,
b
2
]
)
P(X\in [a_1,b_1])=P(X\in [a_2,b_2])
P(X∈[a1,b1])=P(X∈[a2,b2])
那么我们称
X
X
X 服从均匀分布(Uniform)。比方说,我们一般可以假设人在一年中出生的概率是相等的,因此可以用均匀分布来模拟人的出生时间。
| 期望 | 方差 | |
|---|---|---|
| f ( x ; a , b ) = { 1 b − a for x ∈ [ a , b ] 0 otherwise f(x;a,b) = \left\{\begin{array}{ll} \dfrac{1}{b-a} \text{ for } x \in [a,b]\\ 0 \qquad \text{ otherwise } \end{array}\right. f(x;a,b)={b−a1 for x∈[a,b]0 otherwise | a + b 2 \frac{a+b}{2} 2a+b | ( b − a ) 2 12 \frac{(b-a)^2}{12} 12(b−a)2 |
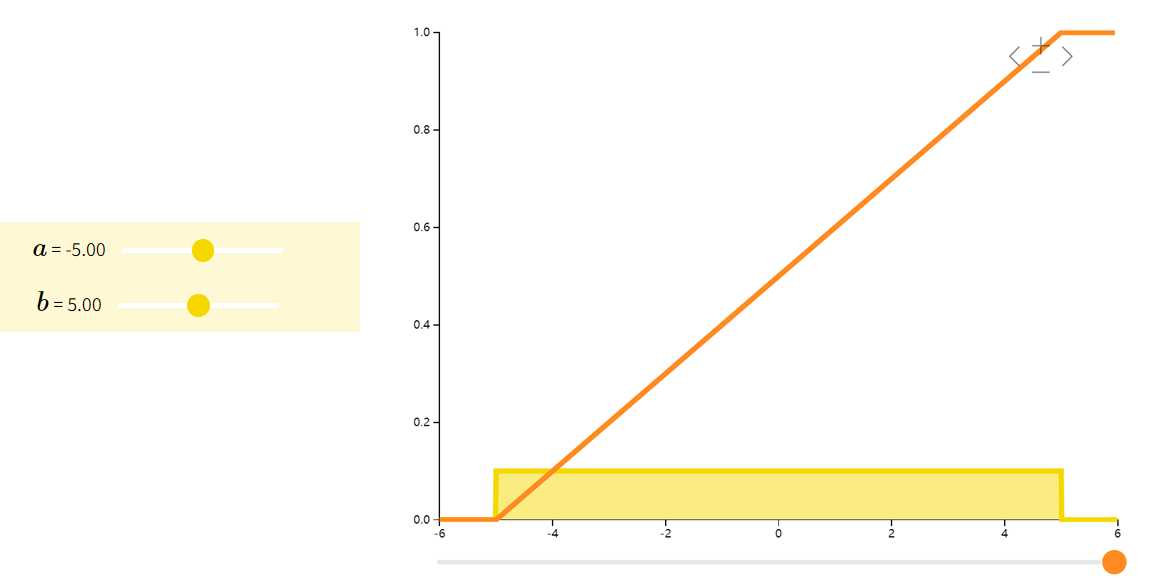
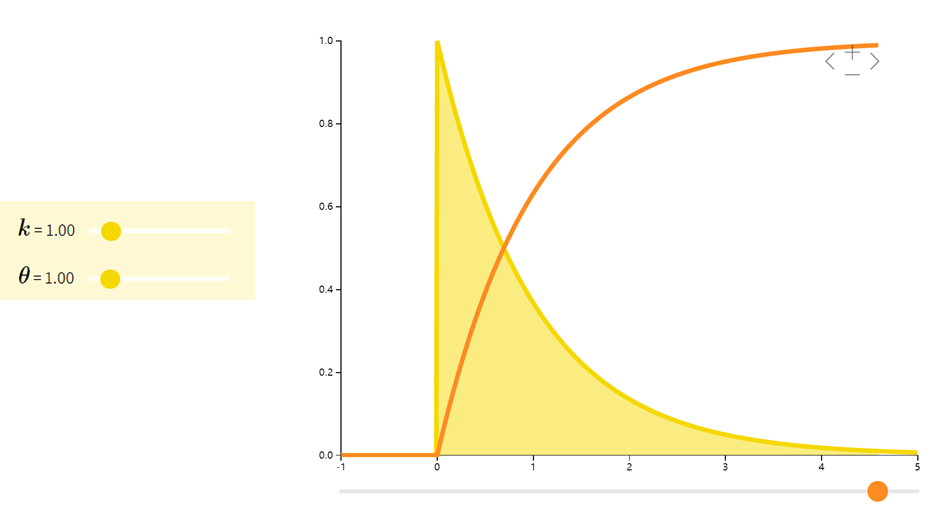
Gamma分布
Gamma分布是一组连续型概率密度。指数分布和卡方分布是Gamma分布的两个特殊情形。
| 期望 | 方差 | |
|---|---|---|
| f ( x ; k , θ ) = 1 Γ ( k ) θ k x k − 1 e − x θ f(x; k,\theta) = \dfrac{1}{\Gamma(k)\theta^{k}}x^{k-1}e^{-\dfrac{x}{\theta}} f(x;k,θ)=Γ(k)θk1xk−1e−θx | k θ k\theta kθ | k θ 2 k\theta^2 kθ2 |
伽玛函数(Gamma函数): Γ ( x ) = ∫ 0 + ∞ t x − 1 e − t d t ( x > 0 ) \Gamma(x)=\int_0^{+∞}t^{x-1} e^{-t}dt(x>0) Γ(x)=∫0+∞tx−1e−tdt(x>0),是阶乘在实数集上的延拓。
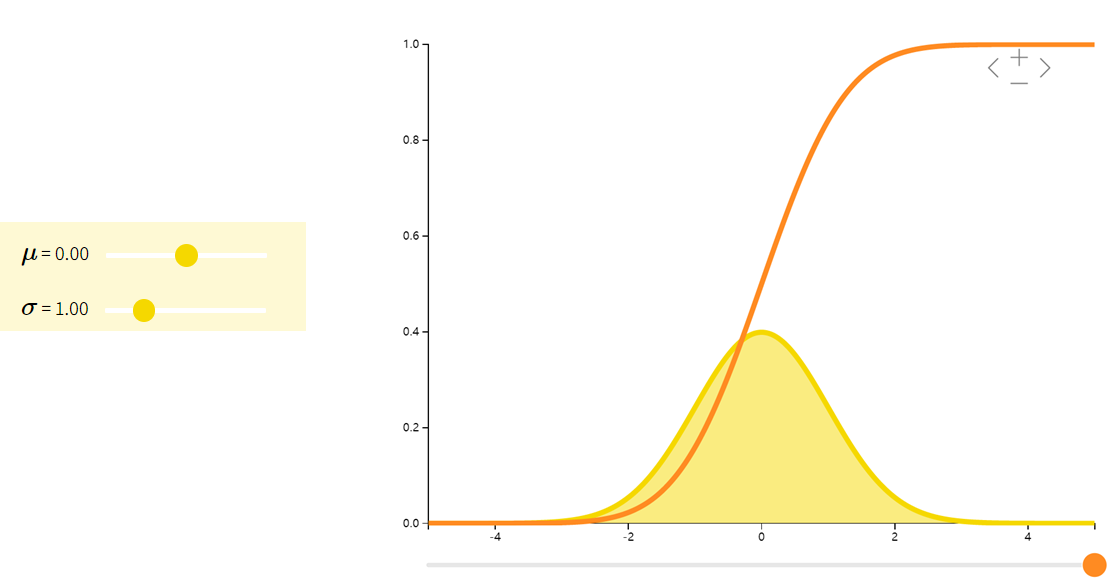
正态分布Normal
正态分布(也称高斯分布)的密度函数是一个钟形曲线。科学中常用正态分布来模拟许多小效应的叠加。比方说,我们知道人的身高是许多微小的基因和环境效应的叠加。因此可以用正态分布来表示人的身高。
| 期望 | 方差 | |
|---|---|---|
| f ( x ; μ , σ 2 ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x;\mu, \sigma^2) = \dfrac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\dfrac{(x-\mu)^{2}}{2\sigma^{2}}} f(x;μ,σ2)=2πσ21e−2σ2(x−μ)2 | μ \mu μ | σ 2 \sigma^2 σ2 |
下面给出正态分布随机变量的一些有用的性质:
如果 X ∼ N ( μ x , σ x 2 ) , Y ∼ N ( μ y , σ y 2 ) X∼N(\mu_x,\sigma_x^2),Y∼N(\mu_y,\sigma_y^2) X∼N(μx,σx2),Y∼N(μy,σy2) 是独立的随机变量。则有:
(a) X + Y ∼ N ( μ x + μ y , σ x 2 + σ y 2 ) X+Y∼N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2) X+Y∼N(μx+μy,σx2+σy2)
(b) a X ∼ N ( a μ x , a 2 σ x 2 ) aX∼N(a\mu_x,a^2\sigma_x^2) aX∼N(aμx,a2σx2)
© X + a ∼ N ( μ x + a , σ x 2 ) X+a∼N(\mu_x+a,\sigma_x^2) X+a∼N(μx+a,σx2)
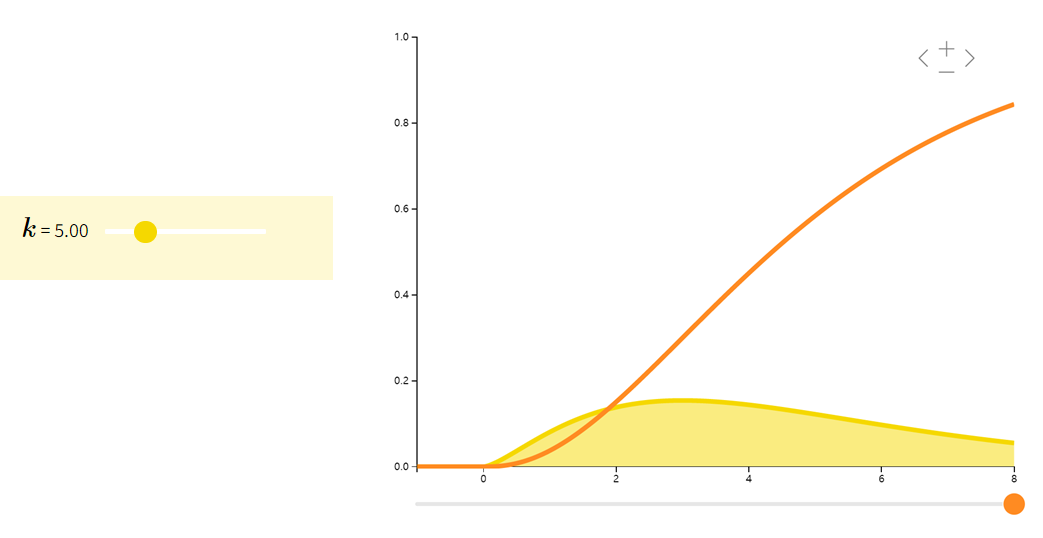
卡方分布Chi Squared
如果随机变量 X X X 是 k k k 个独立的标准正态随机变量的平方和,则称 X X X 为自由度是 k k k 的卡方随机变量: X ∼ χ k 2 X\sim \chi_k^2 X∼χk2。卡方分布常见于假设检验和构造置信区间。
| 期望 | 方差 | |
|---|---|---|
| ∑ i = 1 k Z i 2 Z i ∼ i . i . d . N ( 0 , 1 ) \sum_{i=1}^{k}Z_{i}^{2} \quad Z_{i} \overset{i.i.d.}{\sim} N(0,1) i=1∑kZi2Zi∼i.i.d.N(0,1) | k k k | 2 k 2k 2k |
Student-t 分布
Student-t分布(也称t分布)往往在估计正态总体期望时出现。当我们只有较少的样本和未知的方差时,许多大样本性质并不适用,此时我们则需要用到t分布。
| 期望 | 方差 | |
|---|---|---|
| Z U / k Z ∼ N ( 0 , 1 ) U ∼ χ k \dfrac{Z}{\sqrt{U/k}} \qquad \begin{array}{ll} Z \sim N(0,1)\\ U \sim \chi_{k} \end{array} U/kZZ∼N(0,1)U∼χk | 0 0 0 | k k − 2 \frac{k}{k-2} k−2k |
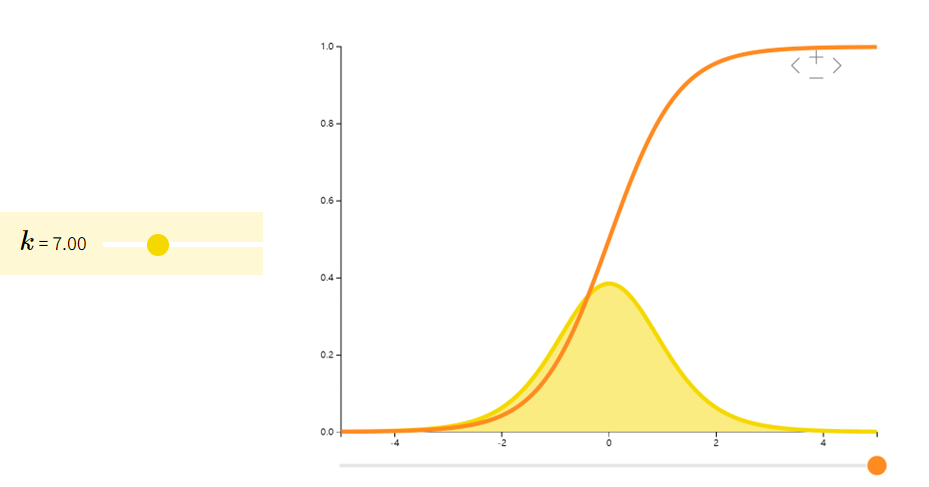
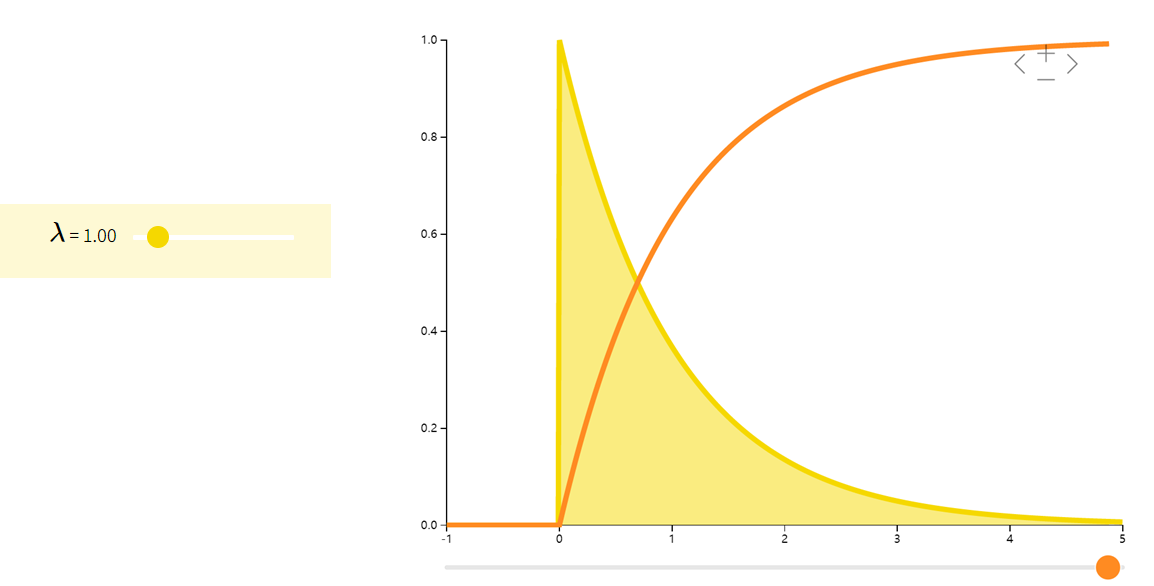
指数分布Exponential
指数分布可以看作是几何分布的连续版本,其常用于描述等待时间。具有无记忆性 P ( X > a + b ∣ X > a ) = P ( X > b ) P(X>a+b|X>a)=P(X>b) P(X>a+b∣X>a)=P(X>b)。
| 期望 | 方差 | |
|---|---|---|
| ( f ( x ; λ ) = { λ e − λ x if x ≥ 0 0 otherwise ( f(x;\lambda) = \begin{cases} \lambda e^{-\lambda x} & \text{if } x \geq 0 \\ 0 & \text{otherwise} \end{cases} (f(x;λ)={λe−λx0if x≥0otherwise | 1 λ \frac{1}{\lambda} λ1 | 1 λ 2 \frac{1}{\lambda^2} λ21 |
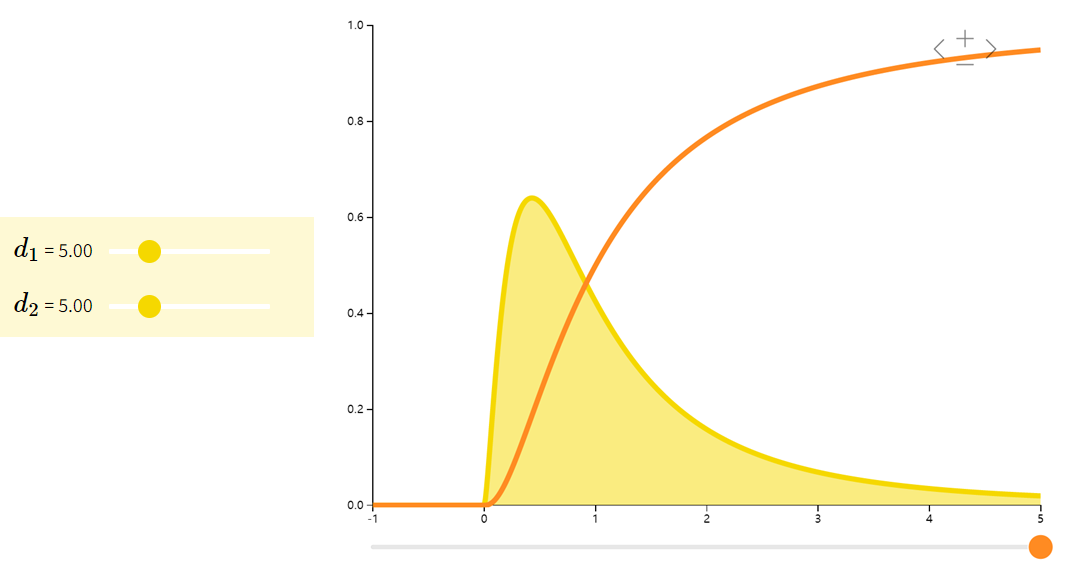
F分布Fisher–Snedecor
它是两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布,是一种非对称分布,且位置不可互换。F分布有着广泛的应用,如在方差分析、回归方程的显著性检验中都有着重要的地位。
| 期望 | 方差 | |
|---|---|---|
| U 1 / d 1 U 2 / d 2 U 1 ∼ χ d 1 U 2 ∼ χ d 2 \dfrac{U_{1}/d_{1}}{U_{2}/d_{2}} \quad \begin{array}{ll} U_{1} \sim \chi_{d_{1}}\\ U_{2} \sim \chi_{d_{2}} \end{array} U2/d2U1/d1U1∼χd1U2∼χd2 | d 2 d 2 − 2 \dfrac{d_{2}}{d_{2}-2} d2−2d2 | 2 d 2 2 ( d 1 + d 2 − 2 ) d 1 ( d 2 − 2 ) 2 ( d 2 − 4 ) \dfrac{2d_{2}^{2}(d_{1} + d_{2} -2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)} d1(d2−2)2(d2−4)2d22(d1+d2−2) |
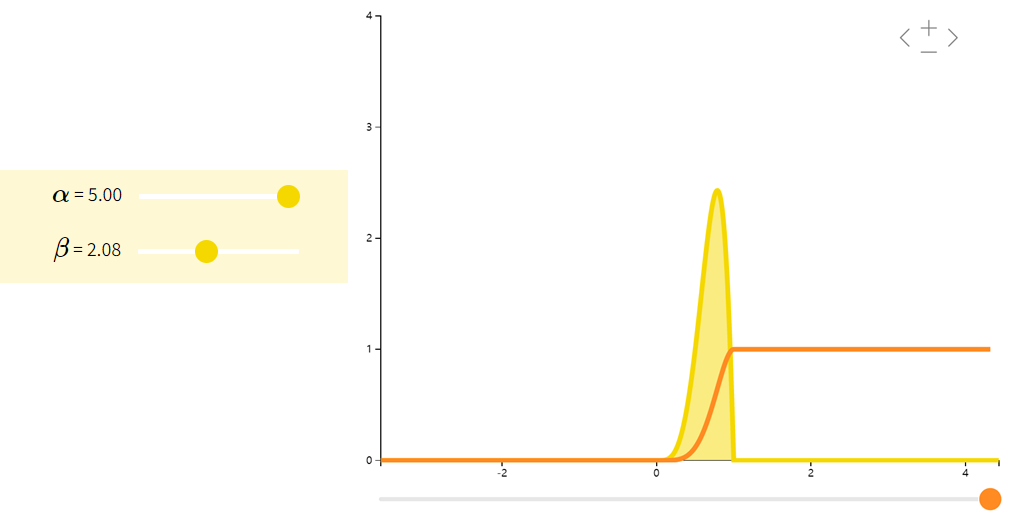
beta分布
Beta分布是一族在 [ 0 , 1 ] [0,1] [0,1]上的连续型概率分布,常用于贝叶斯统计中的共轭先验分布。
| 期望 | 方差 | |
|---|---|---|
| f ( x ; α , β ) = Γ ( α + β ) x α − 1 ( 1 − x ) β − 1 Γ ( α ) Γ ( β ) f(x;\alpha,\beta) = \dfrac{\Gamma(\alpha + \beta)x^{\alpha - 1}(1-x)^{\beta - 1}}{\Gamma(\alpha)\Gamma(\beta)} f(x;α,β)=Γ(α)Γ(β)Γ(α+β)xα−1(1−x)β−1 | α α + β \dfrac{\alpha}{\alpha + \beta} α+βα | α β ( α + β ) 2 ( α + β + 1 ) \dfrac{\alpha\beta}{(\alpha + \beta)^{2}(\alpha + \beta + 1)} (α+β)2(α+β+1)αβ |
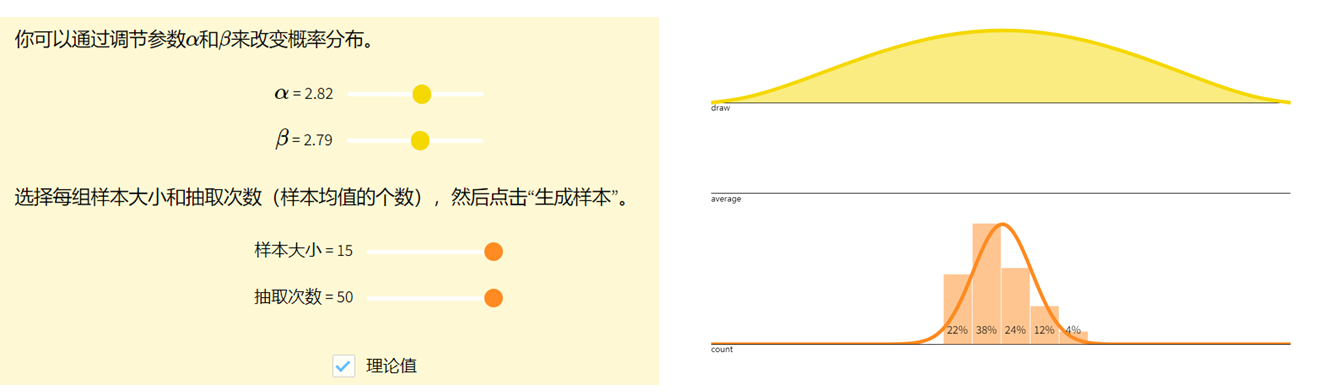
中心极限定理Central Limit Theorem
回到掷骰子的问题。假设你掷了50次骰子,并将平均掷出量记录 X ‾ 1 = 1 50 ∑ k = 1 50 X k \overline{X}_1=\frac{1}{50}\sum_{k=1}^{50}X_k X1=501∑k=150Xk。现在你重复这个实验,将平均掷出量记录为 X ‾ 2 \overline{X}_2 X2。继续这样做,得到一连串的样本平均值 X ‾ 1 , X ‾ 2 , X ‾ 3 ⋯ \overline{X}_1,\overline{X}_2,\overline{X}_3\cdots X1,X2,X3⋯。 如果你画出结果的直方图,你会开始注意到平均值 X ‾ i \overline{X}_i Xi 的分布开始呈现正态。这个近似正态分布的平均值和方差是多少?它们应该与我们下面计算的 X ‾ i \overline{X}_i Xi 的平均值和方差一致。请注意,这些计算并不取决于下标 i i i,因为每个 X ‾ i \overline{X}_i Xi都是由50个独立的公平骰子掷出的样本平均值。因此,我们省略下标 i i i,只是将样本平均值表示 X ‾ = 1 50 ∑ k = 1 50 X k \overline{X}=\frac{1}{50}\sum_{k=1}^{50}X_k X=501∑k=150Xk。
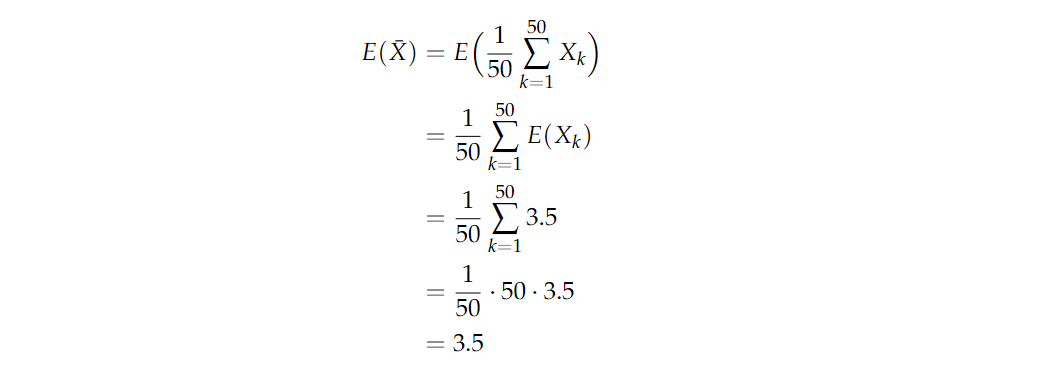
其中掷骰子的期望值为3.5,方差约为2.92。方差计算如下:

所以我们会开始观察到,样本平均数的序列开始类似于期望 μ = 3.5 μ=3.5 μ=3.5 ,方差 σ 2 = 0.0582 σ^2=0.0582 σ2=0.0582的正态分布。这个结果是由中心极限定理得出的,该定理陈述如下。
📏 定理:中心极限定理(Central Limit Theorem):让
X
1
,
X
2
,
X
3
,
⋯
X_1,X_2,X_3,\cdots
X1,X2,X3,⋯是独立同分布的,平均值为
μ
\mu
μ ,方差为
σ
2
\sigma^2
σ2。则有:
X
‾
→
N
(
μ
,
σ
2
n
)
\overline{X}\to N(\mu,\frac{\sigma^2}{n})
X→N(μ,nσ2)
n
→
∞
n→∞
n→∞。
这个定理的意思是,随着样本数量 n n n 的增加,样本均值 X ‾ \overline{X} X 的独立观测值看起来就像是从具有均值 μ μ μ 和方差 σ 2 \sigma^2 σ2 的正态分布中提取出来的然而,这一结果对于 X i X_i Xi 的任何潜在分布都是正确的
📐 推论:中心极限定理的另一种写法为:
X
‾
−
μ
σ
/
n
→
N
(
0
,
1
)
\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\to N(0,1)
σ/nX−μ→N(0,1)
也说明,当n很大时,随机变量
Y
n
=
∑
i
=
1
n
X
i
−
n
μ
n
σ
Y_n = \frac{\sum_{i=1}^nX_i-n\mu}{\sqrt{n}\sigma}
Yn=nσ∑i=1nXi−nμ
近似地服从标准正态分布
N
(
0
,
1
)
N(0,1)
N(0,1)。因此,当n很大时,
∑
i
=
1
n
X
i
=
n
σ
Y
n
+
n
μ
\sum_{i=1}^{n}X_i=\sqrt{n}\sigma Y_n + n\mu
i=1∑nXi=nσYn+nμ
近似地服从正态分布
N
(
n
μ
,
n
σ
2
)
N(nμ,nσ^2)
N(nμ,nσ2)。该定理是中心极限定理最简单又最常用的一种形式,在实际工作中,只要n足够大,便可以把独立同分布的随机变量之和当作正态变量。这种方法在数理统计中用得很普遍,当处理大样本时,它是重要工具。
图示
中心极限定理告诉我们,对于一个(性质比较好的)分布,如果我们有足够大的独立同分布的样本,其样本均值会(近似地)呈正态分布。样本数量越大,其分布与正态越接近。
![[oeasy]python0088_字节_Byte_存储单位_KB_MB_GB_TB](https://img-blog.csdnimg.cn/img_convert/4e15f43aa93478ff245eef53f12c5d3a.jpeg)




![[python入门㊾] - python异常中的断言](https://img-blog.csdnimg.cn/16caf23859fc4edaa7d57b6b747d0432.png)