1.OCR--文本检测算法FCENet

文章目录

- 1.简介
- 2.主要工作
- - 2.1 傅里叶轮廓嵌入(Fourier Contour Embedding)
  - 2.2 `FCE`模型
  - 3.代码实现
- 参考资料

欢迎访问个人网络日志🌹🌹知行空间🌹🌹

论文:Fourier Contour Embedding for Arbitrary-Shaped Text Detection

1.简介

这篇文章是华南理工大学的Yiqin Zhu在2021年04月份发表的有关OCR中做文本检测的工作。一般OCR工作分两步，一步是对文本区域进行检测，先得到文本区域，然后再将检测的文本区域转化成文本。

文本检测的复杂性在于文本区域的步规则性和多样性，常用的在图像空间域做文本检测方法有掩码，像素的笛卡尔或极坐标坐标轮廓点。使用掩码来做需要对图像进行像素级分类后处理时间较长，使用轮廓像素点在处理弯曲文本区域时略显无力。文本检测的方法可粗略的分成基于分割的方法和基于回归的方法。

作者提出的方法在频域对文本区域做检测，使用Fourier Contour Embedding(FCE)方法来表示任意行状的文本轮廓。FCENet模型中使用了骨干网络(backbone)，特征金字塔往略(Feature Pyramid Network)，带傅里叶逆变换(Inverse Fourier Transform,IFT)的后处理，和非极大值抑制。FCENet最大的创新在于其使用神经网络直接对文本轮廓点的傅里叶变换做预测，然后再使用IFT求得最后的文本轮廓。

使用 $k$ 表示傅里叶级数的项数，可以看到随着 $k$ 的增加，引入了更多的高频信号，轮廓刻画的就更准确。

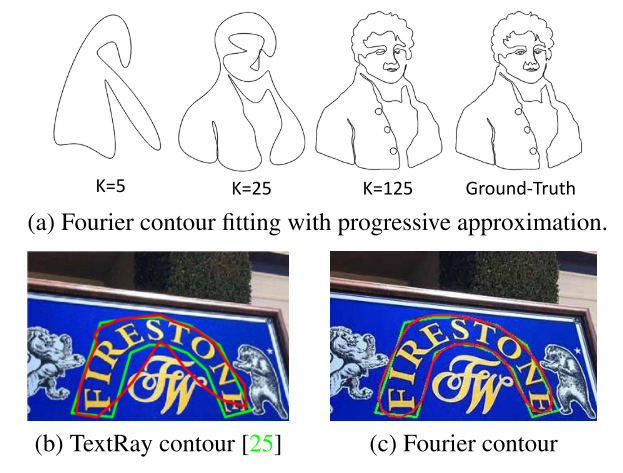
在这里插入图片描述

从上图(a)中可以看到，当 $k = 125$ 时所刻画的轮廓已经十分接近真实的图像了。图(b)和图©中红色轮廓线分别是使用TextRay和FCENet来做文本检测所得到的结果，绿色的是真实的文本轮廓线，可以看到对弯曲的文本，FCENet检测效果更好。

2.主要工作

2.1 傅里叶轮廓嵌入(Fourier Contour Embedding)

对于图像中使用像素坐标点 $(x, y)$ 表示的轮廓，可以使用复数函数 $f:\mathbb{R}\mapsto \mathbb{C}$ 来表示, $f$ 定义成关于实值 $t,t\in[0,1]$ 变化的形式，

$f (t) = x (t) + i y (t)$

其中 $i$ 是复数的虚部单元， $(x (t), y (t))$ 表示 $t$ 时刻轮廓线上的某个空间坐标点， $f$ 表示封闭轮廓时， $f (t) = f (t + 1)$ 。

到这里轮廓线上点的坐标 $(x, y)$ 就被表示成了一系列的复数 $x + i y$ , 我们知道使用傅里叶变换可将函数从时域变换到频率域，因此，同样可以对复数做傅里叶变换和反变换。

若已经知道 $f (t)$ 的傅里叶变换，那么可以通过傅里叶反变换(Inverse Fourier Transformation,IFT)来求 $f (t)$ ,使用傅里叶反变换来表示 $f (t)$ 为：

$\mathbf{c}) = \sum_{k=-\infty}^{+\infty}{\mathbf{c}_ke^{2\pi i k t}}$

其中， $k\in\mathbb{Z}$ 整数表示频率， $c_k$ 是对应频率的傅里叶级数的系数 $c_k$ 是复数，傅里叶级数的每一项 $\mathbf{c}_ke^{2\pi ikt}$ 可以看成以初始方向向量 $\mathbf{c}_k$ 固定频率 $k$ 表示的圆周运动，如此轮廓就可以看成是无数个圆周运动的叠加。

在这里插入图片描述

图像中的轮廓曲线一般很难得到其函数表示 $f$ ,因此可以在轮廓上离散采样 $N$ 个点来表示轮廓(上图中的绿色点)，第 $n$ 个轮廓点可以使用 $f(\frac{n}{N}),n\in[1,...,N]$ 来表示，那么傅里叶系数 $\mathbf{c}_k$ 可写成：

$\mathbf{c}_k=\frac{1}{N}\sum_{n=1}^{N}f(\frac{n}{N})e^{-2\pi ik\frac{n}{N}}$

利用欧拉公式， $\mathbf{c}_k$ 可写成复数形式:

$\mathbf{c}_k = u_k+iv_k$
$u_k,v_k$ 分别表示复数的实部和虚部。

当 $k = 0$ 时， $\mathbf{c}_0=u_0+iv_0=\frac{1}{N}\sum\limits_{n=1}^{N}f(\frac{n}{N})$ ，因此 $c_0$ 表示轮廓的中心。对于任意的轮廓 $f$ ,使用傅里叶变换可将其压缩表示成 $2 (2 K + 1)$ 的向量 $u_{-K},v_{-K},...,u_0,v_0,...,u_K,v_K]$ ,这个向量也被称之为傅里叶签名向量(Fourier Signature Vector)。

傅里叶轮廓嵌入算法(Fourier Contour Embedding）算法分两步，第一步是对轮廓进行采样离散化，譬如在轮廓上均匀采样400个点 $N = 400$ ,可以得到一个包含400个点的轮廓采样点序列 $[f(\frac{1}{N}),...,f(1)]$ ，通过这一步采样，可以使得FCE算法支持更多的数据集合，因为不同数据集标注的文本区域轮廓点的数目并不一样。第二步就是进行傅里叶变换和反变换，求目标值和文本区域的检测框坐标。

采样策略：

采样起始点 $f (0)$ 为，过轮廓中心点 $u_0,v_0)$ 的水平线与轮廓右侧的交点
采样方向，顺时针
匀速，每两个采样点的距离相同

可以通过一段代码来看：

import numpy as np
import matplotlib.pyplot as plt

x = np.array(list(range(10, 210, 10)))
y = np.array([10]*len(x))
x = x[:,None]
y = y[:,None]
pnts = np.concatenate((x,y), axis=-1)

y = np.array(list(range(20, 120, 10)))
x = np.array([200]*len(y))
x[5] = 220
x[6] = 214
x[7] = 207
x[8] = 203

x = x[:,None]
y = y[:,None]
tmp_pnts = np.concatenate((x,y), axis=-1)
pnts = np.vstack((pnts, tmp_pnts))

x = np.array(list(range(190, 0, -10)))
y = np.array([110]*len(x))
x = x[:,None]
y = y[:,None]
tmp_pnts = np.concatenate((x,y), axis=-1)
pnts = np.vstack((pnts, tmp_pnts))

y = np.array(list(range(100, 10, -10)))
x = np.array([10]*len(y))
x = x[:,None]
y = y[:,None]
tmp_pnts = np.concatenate((x,y), axis=-1)
pnts = np.vstack((pnts, tmp_pnts))

pt1 = pnts[:24,:]
pt2 = pnts[24:,:]
pts = np.vstack((pt2, pt1))

complex_pts = pts[:, 0] + pts[:, 1]*1j
ft_pts = np.fft.fft(complex_pts)

approx_ft_pts = np.zeros_like(ft_pts)
# 信号主要由高频和低频组成，中间频率所占很少
approx_ft_pts[:6] = ft_pts[:6] # 低频信号恢复大致轮廓
approx_ft_pts[-5:] = ft_pts[-5:] #高频信号恢复准确轮廓
appox_pts = np.fft.ifft(approx_ft_pts)

# help(plt.plot)
plt.figure(num=1, figsize=(4.5,3), dpi=200)
x = pts[:, 0]
y = pts[:, 1]
plt.plot(x,y,'g-', label='ground truth', linewidth=1 )
x = [e.real for e in appox_pts]
y = [e.imag for e in appox_pts]

plt.plot(x,y,'r-', label='approx truth', linewidth=1 )
plt.legend()
plt.show()

在这里插入图片描述

上图中，绿色的表示实际形状，红色的表示经傅里叶变换和反变换后，只保留 $K = 5$ 个频率的分量而得到的轮廓尺寸，可以看到这能极大的压缩表示轮廓的参数数量,同时还能对轮廓进行较好的近似。

2.2 `FCE`模型

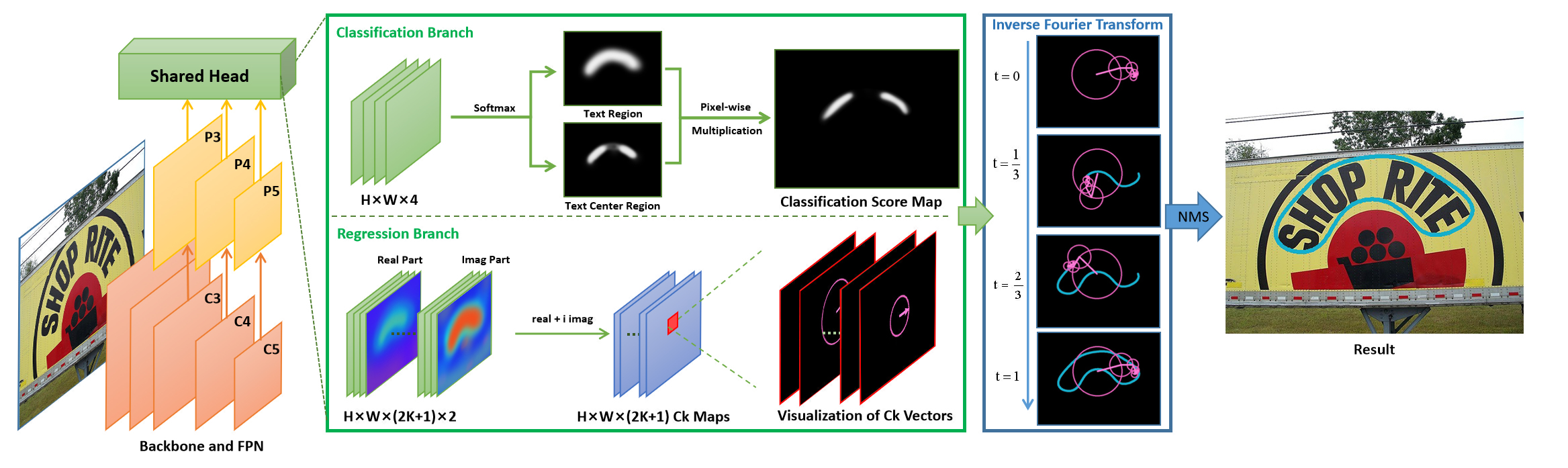
在这里插入图片描述

FCENet的结构同常规的检测模型，其backbone由使用可变形卷积DCN的ResNet50组成，FPN用来提取多尺度的特征，检测头使用以上介绍的傅里叶方法实现。

如上图，检测头由分类和回归两个分支组成，分类分支中，输出的结果通道数是4,前两个通道表示的是每个像素是否是文本区域(Text Region，TR)的概率，后两个通道表示的是每个像素是否是文本中心区域(Text Center Region)的概率，分类分支相当于是分割得到文本区域，然后求文本区域的轮廓中心。

回归分支的通道数 $22$ ，表示的是取傅里叶展开的自由度 $k = 5$ ，取前5个高频和低频及 $k = 0$ 共 $11$ 个复数傅里叶系数，复数使用 $u_k,v_k)$ 来表示，因此总共 $22$ 个变量，通过使用傅里叶逆变换求得最后的检测结果。

3.代码实现

见mmocr: mmocr/models/textdet/postprocessors/fce_postprocessor.py

class FCEPostprocessor(BaseTextDetPostProcessor):
     def __init__(self, **args)：
          ...
     def _get_text_instances_single(self, pred_result: Dict, scale: int):
          """Get text instance predictions from one feature level.

          Args:
               pred_result (dict): A dict with keys of ``cls_res``, ``reg_res``
                    corresponding to the classification result and regression
                    result computed from the input tensor with the same index.
                    They have the shapes of :math:`(1, C_{cls,i}, H_i, W_i)` and
                    :math:`(1, C_{out,i}, H_i, W_i)`.
               scale (int): Scale of current feature map which equals to
                    img_size / feat_size.

          Returns:
               result_polys (list[ndarray]): A list of polygons after postprocess.
               result_scores (list[ndarray]): A list of scores after postprocess.
          """

          cls_pred = pred_result['cls_res']
          tr_pred = cls_pred[0:2].softmax(dim=0).data.cpu().numpy()
          tcl_pred = cls_pred[2:].softmax(dim=0).data.cpu().numpy()

          reg_pred = pred_result['reg_res'].permute(1, 2, 0).data.cpu().numpy()
          x_pred = reg_pred[:, :, :2 * self.fourier_degree + 1]
          y_pred = reg_pred[:, :, 2 * self.fourier_degree + 1:]

          score_pred = (tr_pred[1]**self.alpha) * (tcl_pred[1]**self.beta)
          tr_pred_mask = (score_pred) > self.score_thr
          tr_mask = fill_hole(tr_pred_mask)

          tr_contours, _ = cv2.findContours(
               tr_mask.astype(np.uint8), cv2.RETR_TREE,
               cv2.CHAIN_APPROX_SIMPLE)  # opencv4

          mask = np.zeros_like(tr_mask)

          result_polys = []
          result_scores = []
          for cont in tr_contours:
               deal_map = mask.copy().astype(np.int8)
               cv2.drawContours(deal_map, [cont], -1, 1, -1)

               score_map = score_pred * deal_map
               score_mask = score_map > 0
               xy_text = np.argwhere(score_mask)
               dxy = xy_text[:, 1] + xy_text[:, 0] * 1j

               x, y = x_pred[score_mask], y_pred[score_mask]
               c = x + y * 1j
               c[:, self.fourier_degree] = c[:, self.fourier_degree] + dxy
               c *= scale

               polygons = self._fourier2poly(c, self.num_reconstr_points)
               scores = score_map[score_mask].reshape(-1, 1).tolist()
               polygons, scores = self.poly_nms(polygons, scores, self.nms_thr)
               result_polys += polygons
               result_scores += scores

          result_polys, result_scores = self.poly_nms(result_polys,
                                                       result_scores,
                                                       self.nms_thr)

          if self.text_repr_type == 'quad':
               new_polys = []
               for poly in result_polys:
                    poly = np.array(poly).reshape(-1, 2).astype(np.float32)
                    points = cv2.boxPoints(cv2.minAreaRect(poly))
                    points = np.int0(points)
                    new_polys.append(points.reshape(-1))

               return new_polys, result_scores
          return result_polys, result_scores

     def _fourier2poly(self,
                         fourier_coeff: np.ndarray,
                         num_reconstr_points: int = 50):
          """ Inverse Fourier transform
               Args:
                    fourier_coeff (ndarray): Fourier coefficients shaped (n, 2k+1),
                    with n and k being candidates number and Fourier degree
                    respectively.
                    num_reconstr_points (int): Number of reconstructed polygon
                    points. Defaults to 50.

               Returns:
                    List[ndarray]: The reconstructed polygons.
               """

          a = np.zeros((len(fourier_coeff), num_reconstr_points),
                         dtype='complex')
          k = (len(fourier_coeff[0]) - 1) // 2

          a[:, 0:k + 1] = fourier_coeff[:, k:]
          a[:, -k:] = fourier_coeff[:, :k]

          poly_complex = ifft(a) * num_reconstr_points
          polygon = np.zeros((len(fourier_coeff), num_reconstr_points, 2))
          polygon[:, :, 0] = poly_complex.real
          polygon[:, :, 1] = poly_complex.imag
          return polygon.astype('int32').reshape(
               (len(fourier_coeff), -1)).tolist()