线段树（维护区间信息）

news2024/11/16 0:01:42

一，定义：

可以在logN时间内实现区间修改，单点修改，区间查询等操作的工具

二，思路（修改无乘法时）：

1，建树

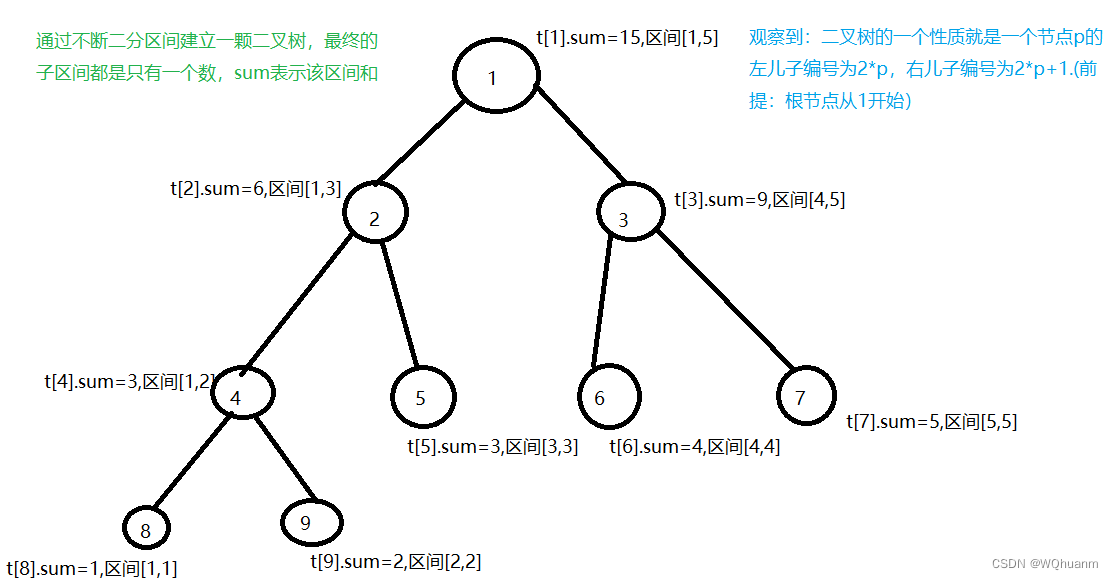
通过把区间不断二分建立一颗二叉树

我们以维护一个数组a={1,2,3,4,5}为例子

int a[N];
struct tree//我们以结构体来存储一颗树
{
	int l, r;//l,r表示该节点的区间
	ll sum, add;//sum表示区间和，add为懒惰标记
} t[N * 4 + 2]; //如果维护n个节点的区间，建立完整的二叉树大概需要4*n个树节点

void build(int l, int r, int p)
{
	t[p].l = l, t[p].r = r; //首先存储节点p的区间
	if (l == r)//如果区间只有一个点
		{
			t[p].sum = a[l];//sum就是这个点的值
			return;
		}
	//否则继续二分遍历
	int mid = l + ((r - l) >> 1);// 移位运算符的优先级小于加减法，所以加上括号,	// 如果写成 (l + r) >> 1 可能会超出 int 范围
	build(l, mid, 2 * p);
	build(mid + 1, r, 2 * p + 1);
	t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后区间和就等于儿子们的区间和之和
}

2，区间修改与懒惰标记

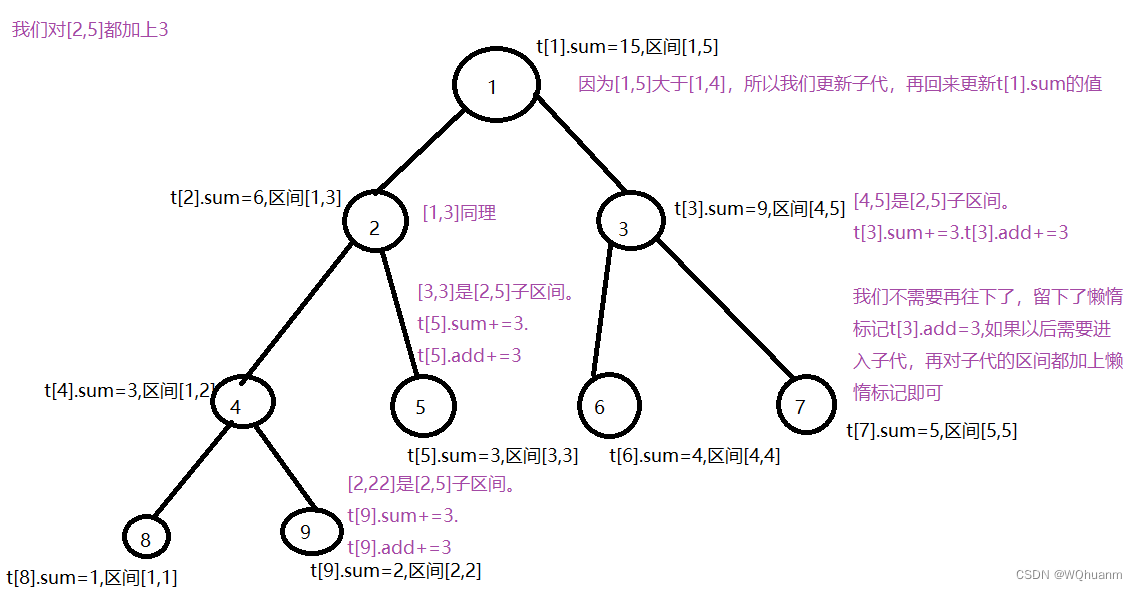
我们思考，如果我们给区间[2,5]都加上3，后面查询的时候只查询过[3,5]。那么请问，我们有没有必要花时间去更新[2,2]有加上3这件事呢。

显然没有必要，所以我们想要偷懒，我可以对你的修改标记一下，只有到我需要用到你时，才去修改他。

方法就是当我们更新一个区间时，我们就对这个区间进行标记（记录其修改的记录），如果后面我们要访问他的子代，我们首先先询问是否这个区间有标记，有则先更新他的子代，才可以去访问子代。

有了懒惰标记，我们每次深入只要深入到当前区间是目标区间子集就可以不用深入了，然后留下懒惰标记即可

void lazy(int p)
{
	if (t[p].l == t[p].r)t[p].add = 0;//如果该区间只有一个点，毫无疑问他没有儿子，直接删除他的懒惰标记
	if (t[p].add)//如果懒惰区间不为0，更新儿子信息
		{
			//对儿子们的区间和更新
			t[2 * p].sum += t[p].add * (t[2 * p].r - t[2 * p].l + 1);
			t[2 * p + 1].sum += t[p].add * (t[2 * p + 1].r - t[2 * p + 1].l + 1);
			//每次更新区间就更新这个区间的懒惰标记，这样儿子访问子代时其懒惰区间才可以正常使用
			t[2 * p].add += t[p].add;
			t[2 * p + 1].add += t[p].add;
			//最后重置p的懒惰标记（他就是为子代存在的，而我们已经更新完子代了）
			t[p].add = 0;
		}
}

void addupdate(int l, int r, int p, ll z)
{
	if (l <= t[p].l && t[p].r <= r)//如果当前p的区间是目标区间的子集，更新其区间值和懒惰标记就可以返回了
		{
			t[p].sum += z * (t[p].r - t[p].l + 1);
			t[p].add += z;
			return;
		}
	//如果不是全部属于目标区间，访问子代前先更新子代，清空自己的懒惰标记
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	if (l <= mid)addupdate(l, r, 2 * p, z);//如果[t[p].l,mid]有一部分属于目标区间，更新[l,mid]
	if (r > mid)addupdate(l, r, 2 * p + 1, z);//[mid+1,t[p].r]同理
	t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后重新更新t[p].sum(因为子代已经更新）
}

3，查询区间（单点值）

和修改的思考差不多，当前区间为目标区间子集就直接访问。否则就更新子代后深入子代

ll ask(int l, int r, int p)
{
	if (l <= t[p].l && t[p].r <= r)return t[p].sum;//属于子集直接返回
	lazy(p);//如果不是全部属于目标区间，访问子代前先更新子代，清空自己的懒惰标记
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	ll ans = 0;//ans累积属于目标区间的和
	if (l <= mid)ans += ask(l, r, 2 * p);
	if (r > mid)ans += ask(l, r, 2 * p + 1);
	return ans;
}

三：模板题1：P3372 【模板】线段树 1

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define int ll
const int N = 1e5 + 10;

int a[N];
struct tree//我们以结构体来存储一颗树
{
	int l, r;//l,r表示该节点的区间
	ll sum, add;//sum表示区间和，add为懒惰标记
} t[N * 4 + 2]; //如果维护n个节点的区间，建立完整的二叉树大概需要4*n个树节点

void build(int l, int r, int p)
{
	t[p].l = l, t[p].r = r; //首先存储节点p的区间
	if (l == r)//如果区间只有一个点
		{
			t[p].sum = a[l];//sum就是这个点的值
			return;
		}
	//否则继续二分遍历
	int mid = l + ((r - l) >> 1);// 移位运算符的优先级小于加减法，所以加上括号,	// 如果写成 (l + r) >> 1 可能会超出 int 范围
	build(l, mid, 2 * p);
	build(mid + 1, r, 2 * p + 1);
	t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后区间和就等于儿子们的区间和之和
}

void lazy(int p)
{
	if (t[p].l == t[p].r)t[p].add = 0;//如果该区间只有一个点，毫无疑问他没有儿子，直接删除他的懒惰标记
	if (t[p].add)//如果懒惰区间不为0，更新儿子信息
		{
			//对儿子们的区间和更新
			t[2 * p].sum += t[p].add * (t[2 * p].r - t[2 * p].l + 1);
			t[2 * p + 1].sum += t[p].add * (t[2 * p + 1].r - t[2 * p + 1].l + 1);
			//每次更新区间就更新这个区间的懒惰标记，这样儿子访问子代时其懒惰区间才可以正常使用
			t[2 * p].add += t[p].add;
			t[2 * p + 1].add += t[p].add;
			//最后重置p的懒惰标记（他就是为子代存在的，而我们已经更新完子代了）
			t[p].add = 0;
		}
}

void addupdate(int l, int r, int p, ll z)
{
	if (l <= t[p].l && t[p].r <= r)//如果当前p的区间是目标区间的子集，更新其区间值和懒惰标记就可以返回了
		{
			t[p].sum += z * (t[p].r - t[p].l + 1);
			t[p].add += z;
			return;
		}
	//如果不是全部属于目标区间，访问子代前先更新子代，清空自己的懒惰标记
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	if (l <= mid)addupdate(l, r, 2 * p, z);//如果[t[p].l,mid]有一部分属于目标区间，更新[l,mid]
	if (r > mid)addupdate(l, r, 2 * p + 1, z);//[mid+1,t[p].r]同理
	t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后重新更新t[p].sum(因为子代已经更新）
}

ll ask(int l, int r, int p)
{
	if (l <= t[p].l && t[p].r <= r)return t[p].sum;//属于子集直接返回
	lazy(p);//如果不是全部属于目标区间，访问子代前先更新子代，清空自己的懒惰标记
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	ll ans = 0;//ans累积属于目标区间的和
	if (l <= mid)ans += ask(l, r, 2 * p);
	if (r > mid)ans += ask(l, r, 2 * p + 1);
	return ans;
}

int32_t main()
{
	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)cin >> a[i];
	build(1, n, 1);//每次都从根节点p=1建树
	int b, l, r, k;
	while (m--)
		{
			cin >> b >> l >> r;
			if (b == 1)
				{
					cin >> k;
					addupdate(l, r, 1, k);//更新，查询也都成根节点p=1开始
				}
			else if (b == 2)
				{
					cout << ask(l, r, 1) << endl;//更新，查询也都成根节点p=1开始
				}
		}
	return 0;
}

 四，思考（如果区间修改同时存在加法和乘法怎么办）

1，我们清楚，乘法就是把当前的区间都*一个值（当然，这个区间是更新过的，因为每次都是更新完这个区间才进入）。

2，我们考虑使用乘法的影响，当我们对当前p的区间乘z时，t[p].sum*=z，那么更新他的懒惰标记

，以子代2*p为例子，他的子代目前是(t[2p]*t[p].mul+t[p].add*size(2p)),我们*z<-->t[2p]*z*t[p].mul*z+t[p].add*z,所以我们一次要更新t[p].mul,t[p].add。

3，我们考虑进入子代前对懒惰标记的处理，我们发现，t[p].add是可以不断用加法与乘法叠加的，而mul一直都是被乘没有加（在进入这一层之前都是这样）。所以我们更新这一层，首先一定要先乘mul在加add。这对t[2*p].sum与t[2*p].add都是一样的，都是先*t[p].mul再加t[p].add

直接上模板题：P3373 【模板】线段树 2

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
#define int ll
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
typedef pair<int, int> pii;

//double 型memset最大127，最小128
//std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
const int INF = 0x3f3f3f3f;         //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 1e5 + 10;

int a[N];
int n, m, mod;
struct tree
{
	int l, r;
	ll sum, add, mul;
} t[4 * N + 2];

void build(int l, int r, int p)
{
	t[p].l = l, t[p].r = r, t[p].mul = 1; //这里多更新了一个mul的初始值是1
	if (l == r)
		{
			t[p].sum = a[l] % mod;
			return;
		}
	int mid = l + ((r - l) >> 1);
	build(l, mid, 2 * p);
	build(mid + 1, r, 2 * p + 1);
	t[p].sum = (t[2 * p].sum + t[2 * p + 1].sum) % mod;
}

void lazy(int p)
{
	if (t[p].l == t[p].r)t[p].add = 0, t[p].mul = 1;
	if (t[p].add || t[p].mul != 1)//只要加法或者乘法有一个存在懒惰标记就更新
		{
			t[2 * p].sum = (t[2 * p].sum * t[p].mul + t[p].add * (t[2 * p].r - t[2 * p].l + 1)) % mod;
			t[2 * p + 1].sum = (t[2 * p + 1].sum * t[p].mul + t[p].add * (t[2 * p + 1].r - t[2 * p + 1].l + 1)) % mod;
			//更新sum与add都是先乘后加
			t[2 * p].add = (t[2 * p].add * t[p].mul + t[p].add) % mod;
			t[2 * p + 1].add = (t[2 * p + 1].add * t[p].mul + t[p].add) % mod;

			t[2 * p].mul = (t[2 * p].mul * t[p].mul) % mod;
			t[2 * p + 1].mul = (t[2 * p + 1].mul * t[p].mul) % mod;
			//重置标记
			t[p].add = 0, t[p].mul = 1;
		}
}

void addupdate(int l, int r, int p, ll z)
{
	if (l <= t[p].l && t[p].r <= r)
		{
			t[p].sum = (t[p].sum + z * (t[p].r - t[p].l + 1)) % mod;
			t[p].add = (t[p].add + z) % mod;
			return;
		}
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	if (l <= mid)addupdate(l, r, 2 * p, z);//只有子代有在目标区间才进入
	if (r > mid)addupdate(l, r, 2 * p + 1, z);
	t[p].sum = (t[2 * p].sum + t[2 * p + 1].sum) % mod;
}

void mulupdate(int l, int r, int p, ll z)
{
	if (l <= t[p].l && t[p].r <= r)
		{
			t[p].sum = (t[p].sum * z) % mod;//乘法需要对p的sum，add,mul都更新
			t[p].add = (t[p].add * z) % mod;
			t[p].mul = (t[p].mul * z) % mod;
			return;
		}
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	if (l <= mid)mulupdate(l, r, 2 * p, z);//只有子代有在目标区间才进入
	if (r > mid)mulupdate(l, r, 2 * p + 1, z);
	t[p].sum = (t[2 * p].sum + t[2 * p + 1].sum) % mod;
}

ll ask(int l, int r, int p)
{
	if (l <= t[p].l && t[p].r <= r)return t[p].sum % mod;
	lazy(p);
	int mid = t[p].l + ((t[p].r - t[p].l) >> 1);
	ll ans = 0;
	if (l <= mid)ans += ask(l, r, 2 * p);
	if (r > mid)ans += ask(l, r, 2 * p + 1);
	return ans % mod;
}

int32_t main()
{
	cin >> n >> m >> mod;
	for (int i = 1; i <= n; ++i)cin >> a[i];
	build(1, n, 1);
	int b, l, r, k;
	while (m--)
		{
			cin >> b >> l >> r;
			if (b == 1)
				{
					cin >> k;
					mulupdate(l, r, 1, k);
				}
			else if (b == 2)
				{
					cin >> k;
					addupdate(l, r, 1, k);
				}
			else if (b == 3)
				{
					cout << ask(l, r, 1) << endl;
				}
		}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/356305.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

流程引擎之compileflow简介

流程引擎之compileflow简介

背景compileflow 是一个非常轻量、高性能、可集成、可扩展的流程引擎。compileflow Process 引擎是淘宝工作流 TBBPM 引擎之一&#xff0c;是专注于纯内存执行&#xff0c;无状态的流程引擎&#xff0c;通过将流程文件转换生成 java 代码编译执行&#xff0c;简洁高效。当前是阿…
阅读更多...
JVM内存布局

JVM内存布局

JVM的主要组成&#xff1a;JVM包含俩个子系统和俩个组件&#xff0c;俩个子系统为Class loader&#xff08;类装载&#xff09;、Execution engine&#xff08;执行引擎&#xff09;&#xff1b;俩个组件为Runtime data area&#xff08;运行时数据区&#xff09;、Native Inte…
阅读更多...
认证全家桶(Cookie、Session、Token、JWT)

认证全家桶(Cookie、Session、Token、JWT)

什么是认证(Authentication) 通俗地讲就是验证当前用户的身份&#xff0c;证明“你是你自己”&#xff08;比如&#xff1a;你每天上下班打卡&#xff0c;都需要通过指纹打卡&#xff0c;当你的指纹和系统里录入的指纹相匹配时&#xff0c;就打卡成功&#xff09;互联网中的认…
阅读更多...
independentsoft.de/MSG .NET Framework Crack

independentsoft.de/MSG .NET Framework Crack

MSG .NET 是用于 .NET Framework / .NET Core 的 Microsoft Outlook .msg 文件 API。API 允许您轻松创建/读取/解析/转换 .msg 文件等。API 不需要在机器上安装 Microsoft Outlook 或任何其他第三方应用程序或库即可工作。 以下示例向您展示了如何打开现有文件并显示消息的某些…
阅读更多...
sklearn学习-线性回归大家族

sklearn学习-线性回归大家族

文章目录一、多元线性回归二、回归类的评估指标三、多重共线性&#xff1a;岭回归和Lasso四、Lasso选取最佳的正则化参数取值总结一、多元线性回归 二、回归类的评估指标 三、多重共线性&#xff1a;岭回归和Lasso 多重共线性 Multicollinearity 与 相关性 Correlation: 多重共…
阅读更多...
达梦8共享存储集群DSC

达梦8共享存储集群DSC

简介&#xff1a; DM 共享存储数据库集群的英文全称 DM Data Shared Cluster&#xff0c;简称 DMDSC。 熟悉Oracle的朋友会知道目前国产数据库只有达梦数据库有共享存储集群架构&#xff0c;Oracle通过私网进行不同节点之间的缓存融合&#xff0c;而达梦通过自己的MAL系统&…
阅读更多...
Java牛客编程刷算法记录--2022-12-7+2023-2-19

Java牛客编程刷算法记录--2022-12-7+2023-2-19

https://www.nowcoder.com/ta/classic-code 牛客上经典必刷题库 https://www.nowcoder.com/practice/e08819cfdeb34985a8de9c4e6562e724?tpId46&tqId29030&rp1&ru/ta/classic-code&qru/ta/classic-code&difficulty&judgeStatus&tags/question-ran…
阅读更多...
Android自动化配置

Android自动化配置

1 搭建APPIUM环境 1.1 安装node.js Appium是使用nodejs实现的&#xff0c;所以node是解释器&#xff0c;需要第一步安装好 node.js的安装包下载地址&#xff1a; https://nodejs.org/en/download/ 注意&#xff1a;node.js的安装包的下载在官网有两种版本&#xff0c;建议大…
阅读更多...
基于FFmpeg实现的无声音屏幕录制

基于FFmpeg实现的无声音屏幕录制

UI自动化测试时&#xff0c;有时需要进行录屏操作&#xff0c;这时我们是不需要声音的&#xff0c;我们可以通过FFmpeg进行简单的录制工作。 以下是在windows10环境下&#xff0c;基于FFmpeg实现的简单录制&#xff1a; Ffmpeg简介&#xff1a; 功能&#xff1a;有非常强大的…
阅读更多...
Spring Cloud Nacos实战（六）- 集群架构说明与持久化配置切换

Spring Cloud Nacos实战（六）- 集群架构说明与持久化配置切换

目录Nacos集群架构说明Nacos支持三种部署模式集群部署说明预备环境Nacos持久化切换配置Nacos持久化配置Nacos默认derby切换MySql测试Nacos集群架构说明 ​ 到目前为止&#xff0c;我们已经对Nacos的一些基本使用和配置已经掌握&#xff0c;但是这些还不够&#xff0c;我们还需…
阅读更多...
算法导论【时间复杂度】—排序算法、图算法、动态规划、字符串匹配等时间复杂度小结

算法导论【时间复杂度】—排序算法、图算法、动态规划、字符串匹配等时间复杂度小结

算法导论【时间复杂度】—排序算法、图算法、DP等小结排序快速排序堆排序计数排序基数排序桶排序SELECT算法RANDOMIZED-SELECTSELECT图算法广度优先搜索深度优先搜索Kruskal算法Prim算法Bellman-Ford算法Dijkstra算法Floyd-Warshall算法Johnson算法Ford-Folkson方法Edmonds-Kar…
阅读更多...
基于Redis实现的分布式锁

基于Redis实现的分布式锁

基于Redis实现的分布式锁什么是分布式锁分布式锁主流的实现方案Redis分布式锁Redis分布式锁的Java代码体现优化一&#xff1a;使用UUID防止误删除优化二&#xff1a;LUA保证删除原子性什么是分布式锁 单体单机部署中可以为一个操作加上锁&#xff0c;这样其他操作就会等待锁释…
阅读更多...
网络安全-FOFA资产收集和FOFA API调用

网络安全-FOFA资产收集和FOFA API调用

网络安全-FOFA资产收集和FOFA API调用 前言 一&#xff0c;我也是初学者记录的笔记 二&#xff0c;可能有错误的地方&#xff0c;请谨慎 三&#xff0c;欢迎各路大神指教 四&#xff0c;任何文章仅作为学习使用 五&#xff0c;学习网络安全知识请勿适用于违法行为 学习网络安全…
阅读更多...
Android OTA升级常见问题的解决方法

Android OTA升级常见问题的解决方法

1.1 多服务器编译 OTA 报错 Android7 以后引入了 jack-server 功能&#xff0c;也导致在公共服务器上 编译 Android7 以上的版本时&#xff0c;会出现 j ack-server 报错问题。 在多用户服务器上 编译 dist 时 会出现编译过程中 会将 port_service 和 port_admin 改为 默认的 …
阅读更多...
Go语言Web入门之浅谈Gin框架

Go语言Web入门之浅谈Gin框架

Gin框架Gin简介第一个Gin示例HelloworldRESTful APIGin返回数据的几种格式Gin 获取参数HTTP重定向Gin路由&路由组Gin框架当中的中间件Gin简介 Gin 是一个用 Go (Golang) 编写的 web 框架。它是一个类似于 martini 但拥有更好性能的 API 框架&#xff0c;由于 httprouter&a…
阅读更多...
MySQl----- 单表查询

MySQl----- 单表查询

表名&#xff1a;worker-- 表中字段均为中文&#xff0c;比如 部门号 工资 职工号 参加工作 等 CREATE TABLE worker ( 部门号 int(11) NOT NULL, 职工号 int(11) NOT NULL, 工作时间 date NOT NULL, 工资 float(8,2) NOT NULL, 政治面貌 varchar…
阅读更多...
【Spark分布式内存计算框架——Spark SQL】11. External DataSource（中）parquet 数据

【Spark分布式内存计算框架——Spark SQL】11. External DataSource（中）parquet 数据

6.3 parquet 数据 SparkSQL模块中默认读取数据文件格式就是parquet列式存储数据&#xff0c;通过参数【spark.sql.sources.default】设置&#xff0c;默认值为【parquet】。 范例演示代码&#xff1a;直接load加载parquet数据和指定parquet格式加载数据 import org.apache.s…
阅读更多...
事物发展的不同阶段会有不同的状态

事物发展的不同阶段会有不同的状态

之前讨论过一个话题&#xff0c;有人问“股票交易稳定盈利很难么&#xff1f;” 我的回答&#xff1a;不难&#xff0c;难在之前。 这几天我又想到经常看到论坛里有人pk观点&#xff0c;最后甩出一句话&#xff1a;“证明你说得对&#xff0c;你先赚一个亿再说。否则&#xf…
阅读更多...
写代码犹如写文章: “大师级程序员把系统当故事来讲，而不是当做程序来写” | 如何架构设计复杂业务系统? 如何写复杂业务代码？...

写代码犹如写文章: “大师级程序员把系统当故事来讲，而不是当做程序来写” | 如何架构设计复杂业务系统? 如何写复杂业务代码？...

“大师级程序员把系统当故事来讲&#xff0c;而不是当做程序来写”写代码犹如写文章好的代码应该如好文章一样表达思想&#xff0c;被人读懂。中心思想: 突出明确程序是开发者用编程语言写成的一本书&#xff0c;首先应该是记录开发者对业务需求分析、系统分析&#xff0c;最终…
阅读更多...
并发编程底层原理

并发编程底层原理

并发编程 文章目录并发编程线程知识点回顾多线程并行和并发什么是并发编程&#xff1f;并发编程的根本原因&#xff1f;Java内存模型&#xff08;JMM&#xff09;并发编程的核心问题-可见性、有序性、原子性可见性有序性原子性并发问题总结volatile关键字volatile的底层原理如何…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023