题目描述
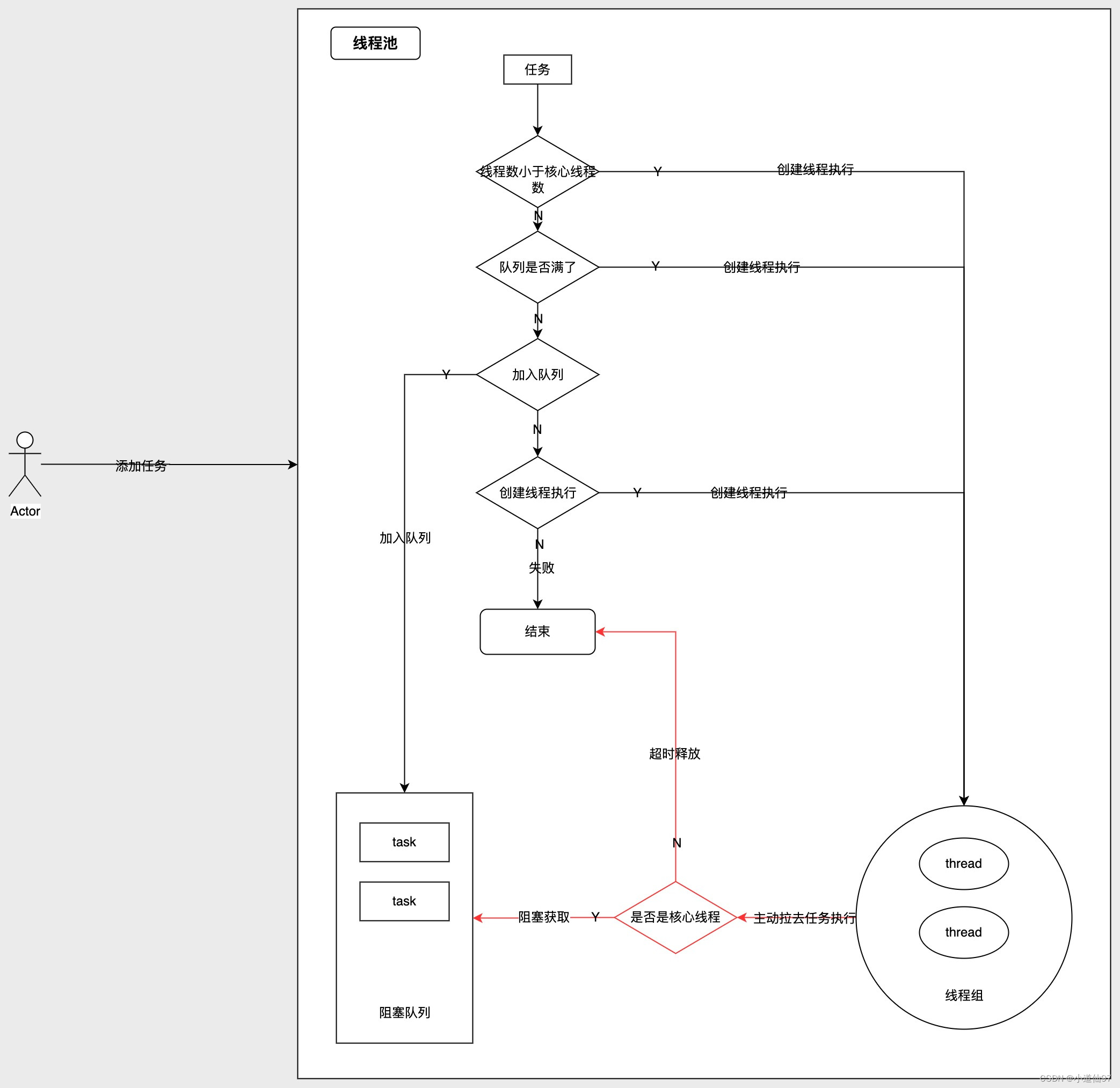
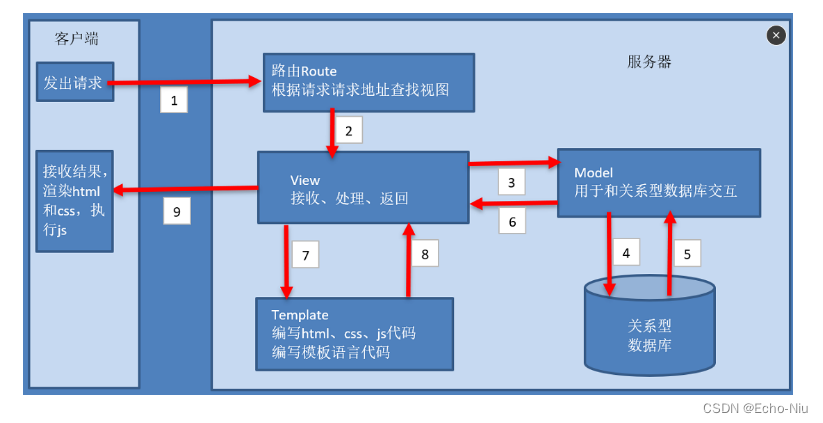
给定一棵包含 N个节点的完全二叉树，树上每个节点都有一个权值，按从 上到下、从左到右的顺序依次是 A_1, A_2, ··· A_N，如下图所示：

现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点 权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入描述
第一行包含一个整数 N（1 ≤N≤ 10^5）N（1≤N≤10^5 ）。
第二行包含 NN 个整数 A_1, A_2, ··· A_N （−10^5 < A_i< 10^5）A 1 ,A 2,⋅⋅⋅AN（−10^5≤Ai≤10^5 ）。

输出描述
输出一个整数代表答案。

输入输出样例
示例
输入

7
1 6 5 4 3 2 1

输出

2

运行限制
最大运行时间：1s
最大运行内存: 256M

所需变量

int n;//用户输入，代表有多少个节点

int temp;//用于接收每次输入的节点信息

int a[20];//代表每层的总数，我直接定义一个20层

int max;//代表每层的最大值

int maxxh;//代表最大的那层的序号

int control;//用于开始判断一共需要多少层

int depth;//代表现在是第几层，来计算现在层数的总和

int sum;//来统计这一层的总和，最后赋值给a数组

我们首先拿到这个题，要判断一下，目前一共有多少层，确定好control，我们才好做下一步动作！部分代码如下：

while(pow(2,control)<=n){
    control++;
  }

现在我们已知他的层数后，我们要每次输入进来，因为我没有用数组存起来，那么每次用temp接收我们就得把他保存起来，当然啦，为什么用temp，是因为为了节省空间开销那么该代码如下：

for(int i = 1;i<=n;i++){
    cin>>temp;
    if(i>=pow(2,depth)){
      a[depth++] = sum;
      sum = 0;
    }
    sum += temp;
  }

上面部分代码的解释就是，每当输入一个temp我们就判断这个数是否属于这一层，如果属于，那么我们就加到sum中，如果是下一层的，那么我们就知道上一层已经结束，那么我们将上一层的总和赋值到a数组中去，然后再将下一层的总和sum赋值为0，重新开始计算下一层的总和！

将上面这些动作做完后，我们就是判断a数组中，那个总和是最大的，这样就可以得到最大的那个数，和最大的那个数的序号，将其赋值给maxxh，最后将maxxh输出出来，整个程序就结束！
该算法本人认为比较优，如果有更好的想法，欢迎q我！

#include <iostream>
#include<math.h>
using namespace std;
int main()
{
  // 请在此输入您的代码
  int n,temp;
  int a[20] = {0},max = 0,maxxh = 0;
  int control = 0,depth = 1;//control代表一共有多少层，depth代表现在在第几层
  int sum = 0;
  cin>>n;
  while(pow(2,control)<=n){
    control++;
  }
  for(int i = 1;i<=n;i++){
    cin>>temp;
    if(i>=pow(2,depth)){
      a[depth++] = sum;
      sum = 0;
    }
    sum += temp;
  }
  a[depth] = sum;
  for(int i = 1;i<=control;i++){
    if(i==1){
      max = a[1];
      maxxh = 1;
    }else{
      if(a[i]>max){
        max = a[i];
        maxxh = i;
      }
    }
  }
  cout<<maxxh<<endl;
  return 0;
}