- 1 有意义数位概念与有意义数位损失
- 1.1 怎么分析误差
- 2 逼近阶 与渐近记法
- 3 误差传播与稳定性
1 有意义数位概念与有意义数位损失
整数的二进制表示使用短除法,网上有很多文章,这里就不再过多赘述了。
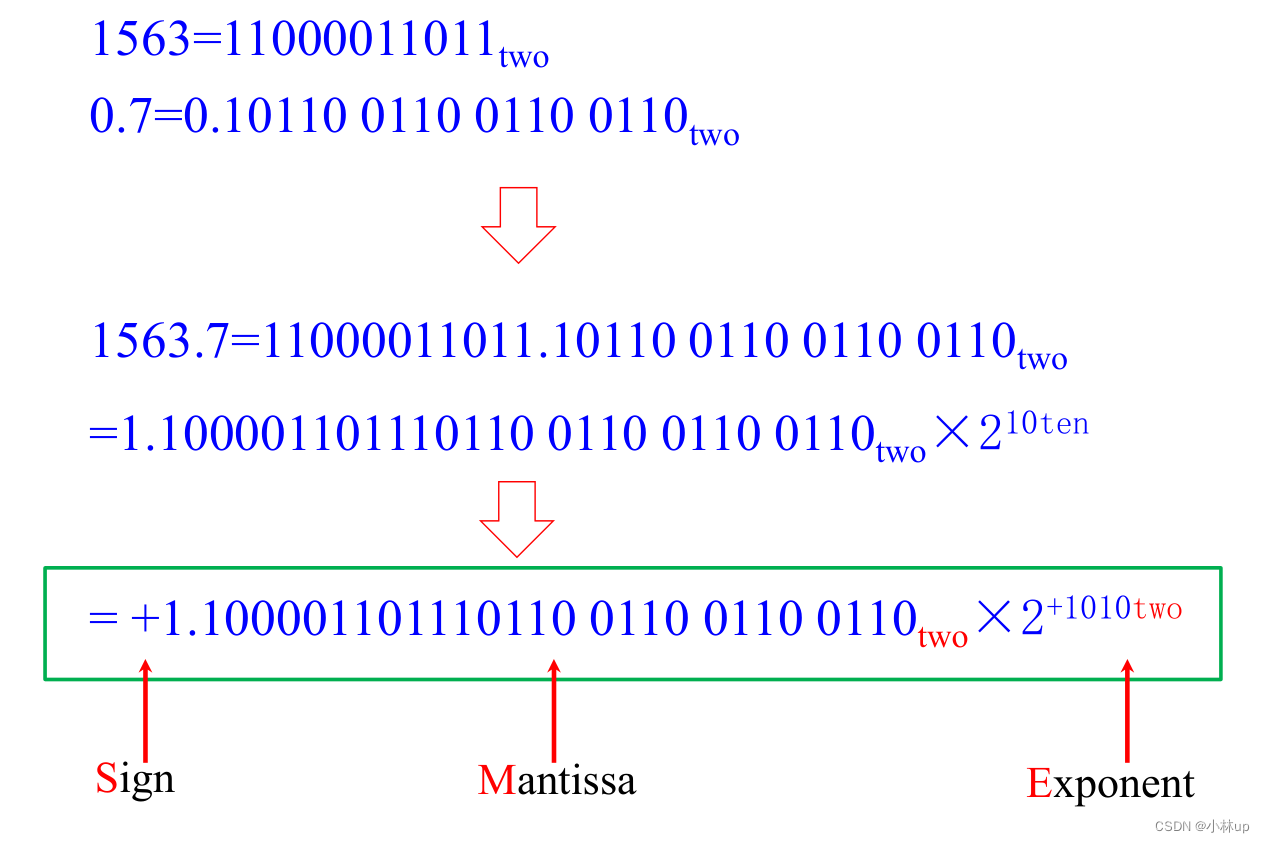
提一嘴小数的二进制表示。下面列举了一个例子。

在表示数位的时候,我们使用一个符号sign,一个尾数mantissa,一个指数exponent。
IEEE-754 double-precision floating-point format给出了数的表示形式。
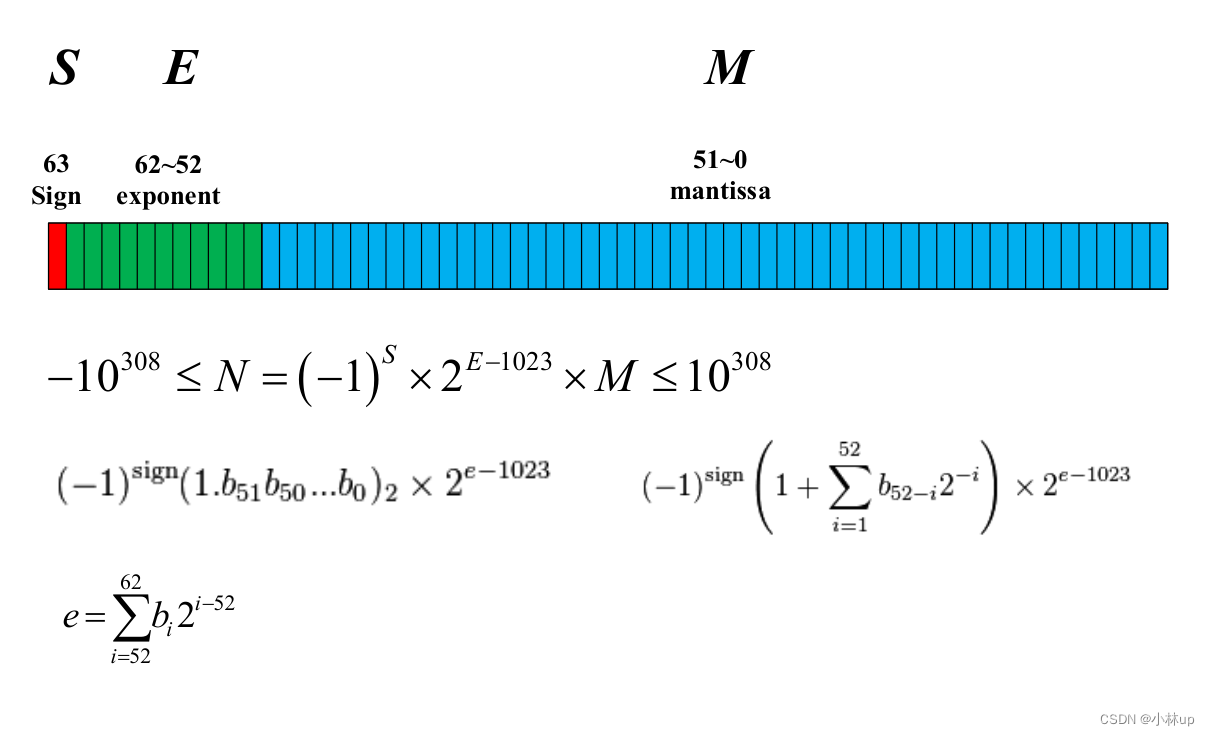
注意这种表示方法是非均匀分布的:

小数在不同的地方可以看到绝对误差是不一样的

然而我们发现相对误差是一样的,除了 0 ≤ x < x ˉ 0 0\le x<\bar{x}_0 0≤x<xˉ0这一段区间。相对误差都是 0.5 × 2 − 53 0.5\times 2^{-53} 0.5×2−53

- 最小正值不是0
- 绝对误差不同
- 相对误差相同,引入机器精度(和尾数长度有关):
m a c h i n e e p s i l o n = 2 − 53 ≈ 1 0 − 16 machine epsilon=2^{-53}\approx {10^{-16}} machineepsilon=2−53≈10−16
所以计算机保存尾数是16位的小数,最大程度低保证了尾数的所有位。
机器数的定义为:尾数的第一个
d
1
=
1
d_1=1
d1=1。
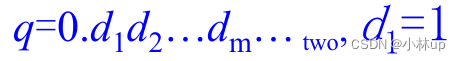
或者写作
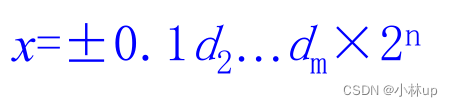
对于计算机来说,尾数的长度m一般是固定的,
- 单精度实数(32位):m=24, n=8。
- 双精度实数(64位):m=53,n=11。
- 但是对于浮点数,二进制小数点的位置一般不是固定的。
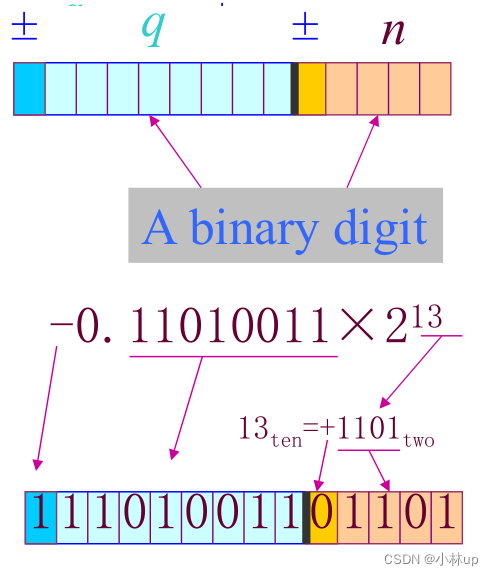
举个例子:
1 10 = 0.0 0011 ‾ two = 0.0 0011 ‾ 001100110011 … t w o \frac{1}{10}=0.0 \overline{0011}_{\text {two }}=0.0 \underline{0011} 001100110011 \ldots_{t w o} 101=0.00011two =0.00011001100110011…two
如果我们规定尾数长度为32位,则 x x x表示为。
x = 0.1100 1100 1100 1100 1100 1100 1100 110 0 t w o × 2 − 3 x=0.1100\,1100\,1100\,1100\,1100\,1100\,1100\,1100_{t w o} \times 2^{-3} x=0.11001100110011001100110011001100two×2−3
于是误差表示为:
e = ∣ 1 10 − x ∣ = 0. 100 ‾ two × 2 − 35 ≈ 2.328306437 × 1 0 − 11 e=\left|\frac{1}{10}-x\right|=0 . \overline{100}_{\text {two }} \times 2^{-35} \approx 2.328306437 \times 10^{-11} e= 101−x =0.100two ×2−35≈2.328306437×10−11
对于24位尾数,8位指数的机器数,表示为:
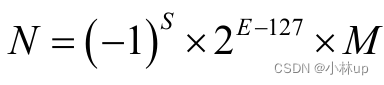
最小分辨率为
2
−
127
2^{-127}
2−127
机器误差举例:

计算精度:
R
=
0.0714
R=0.0714
R=0.0714
机器误差: R m = 0.5 × 2 − 4 ≈ 0.0313 R_{m}=0.5 \times 2^{-4} \approx 0.0313 Rm=0.5×2−4≈0.0313
我们看到 R m < R R_{m}<R Rm<R,这是为什么呢?
1.1 怎么分析误差
x x x是精确数, x ′ x' x′是数值计算的近似数。
定义绝对误差为:
E x = ∣ x − x ′ ∣ \mathrm{E}_{x}=|x-x'| Ex=∣x−x′∣
相对误差为:
R x = ∣ x − x ′ ∣ / ∣ x ∣ \mathrm{R}_{x}=|x-x'| /|x| Rx=∣x−x′∣/∣x∣
有意义的数位 d d d定义为:
R x = ∣ x − x ′ ∣ / ∣ x ∣ < 0.5 × 1 0 1 − d \mathrm{R}_{x}=\left|x-x^{\prime}\right| /|x|<0.5 \times 10^{1-d} Rx=∣x−x′∣/∣x∣<0.5×101−d
例如:
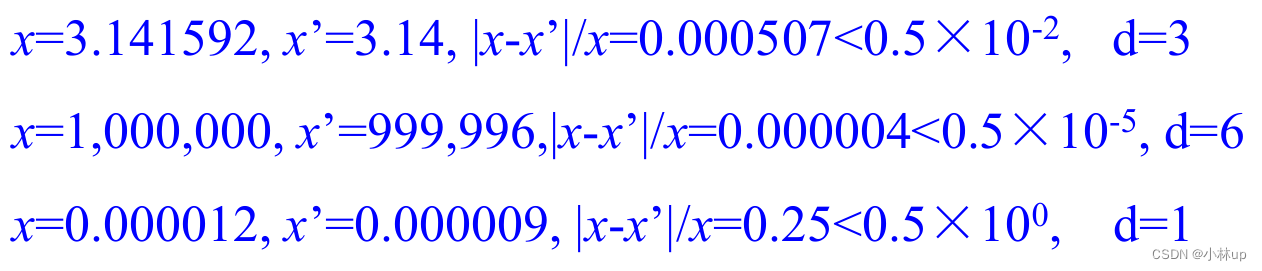
有意义的数位为相对误差定义了一个离散的数字精度等级。它有什么用呢?
好比:
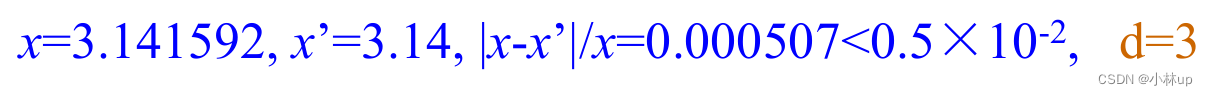
d=3。于是3.141592近似数3.14的前三位都是有效数字:3.14。
而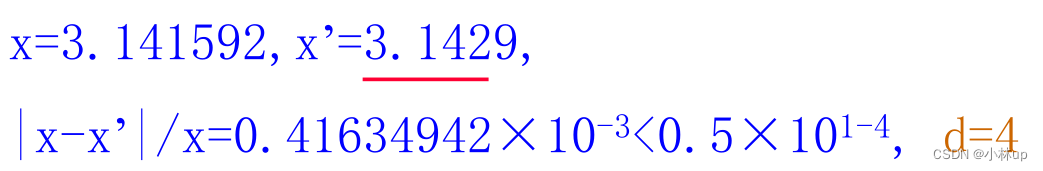
d=4。于是3.141592近似数3.1429的前四位3是有效数字:3.142。
对有意义数位的直观解释:
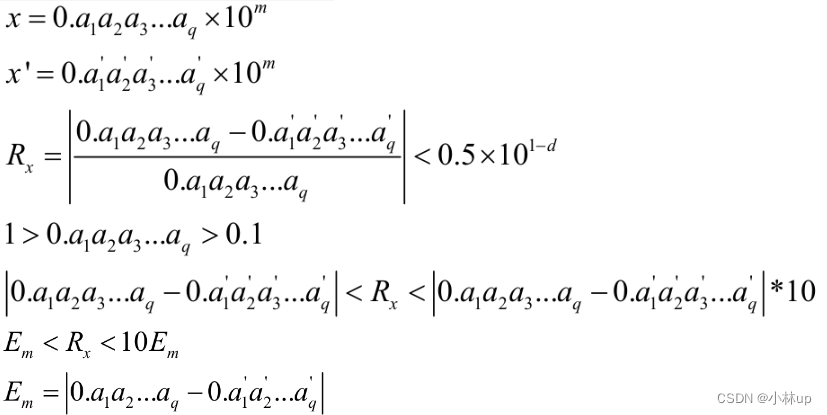
这表明虽然 R x R_x Rx不能反映在数字的表示中,但是可以通过绝对误差 E m E_m Em来反映(注意小数表示的十分位不能是0)。
另外要注意的是有意义的数位是从左往右第一个非零数字开始的:
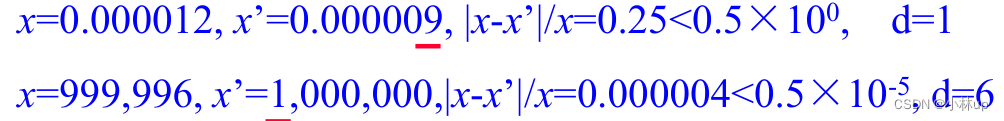
根据上面的表达式我们有:
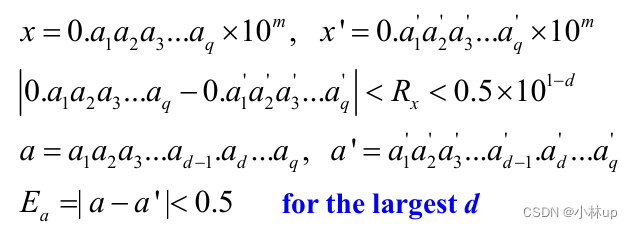
在最后一个式子中 E a = ∣ a − a ′ ∣ < 0.5 E_{a}=\left|a-a^{\prime}\right|<0.5 Ea=∣a−a′∣<0.5我们看到已经和m没有关系了。
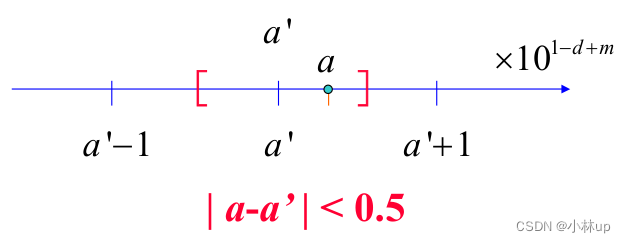
我们把
R
x
R_x
Rx得到的有意义数位记作
d
R
x
d_{R_x}
dRx【相对误差引起】,把
E
m
E_m
Em得到的有意义的数位记作
d
E
m
d_{E_m}
dEm【尾数误差引起】。参见下面的例子我们得到:
d
E
m
=
d
R
x
+
1
d_{E_{m}}=d_{R_{x}}+1
dEm=dRx+1

看一下不同的尾数保留:

根据
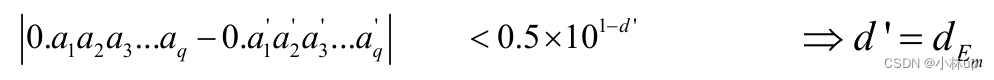
我们让
d
=
d
′
−
1
=
d
E
m
−
1
d=d^{\prime}-1=d_{E_m}-1
d=d′−1=dEm−1作为有效数字,于是有:
∣ 0. a 1 a 2 a 3 … a q − 0. a 1 ′ a 2 ′ a 3 ′ … a q ′ ∣ < 0.5 × 1 0 − d ⇔ E = ∣ x − x ′ ∣ < 0.5 × 1 0 m − d ( 注意 x ′ = ± 0 ⋅ a 1 a 2 … a n × 1 0 m , a 1 ! = 0 ) \begin{array}{l} \left|0 . a_{1} a_{2} a_{3} \ldots a_{q}-0 . a_{1}^{\prime} a_{2}^{\prime} a_{3}^{\prime} \ldots a_{q}^{\prime}\right| \quad<0.5 \times 10^{-d} \\ \Leftrightarrow E=\left|x-x^{\prime}\right|<0.5 \times 10^{m-d}\quad(注意x^{\prime}=\pm 0 \cdot a_{1} a_{2} \ldots a_{n} \times 10^{m}, a_{1} !=0) \end{array} 0.a1a2a3…aq−0.a1′a2′a3′…aq′ <0.5×10−d⇔E=∣x−x′∣<0.5×10m−d(注意x′=±0⋅a1a2…an×10m,a1!=0)
下面来区分一下有意义数位(significant digit)和有效数字(effective digit):

尽管他们的定义不一样,但是一般他们的数值是相等的(用到了 d = d E m − 1 和 d E m = d R x + 1 d=d_{E_{m}}-1和d_{E_{m}}=d_{R_{x}}+1 d=dEm−1和dEm=dRx+1推得: d = d R x d=d_{R_{x}} d=dRx)。

如果我们知道 d d d和 m m m就可以推知 E E E的范围:

如果我们知道
E
E
E和
m
m
m就可以知道近似数
x
′
x'
x′多少位是有用的


误差来源:
- 数学表达式的误差

- 舍入和近似误差

3. 算术误差

2 逼近阶 与渐近记法
大O记号
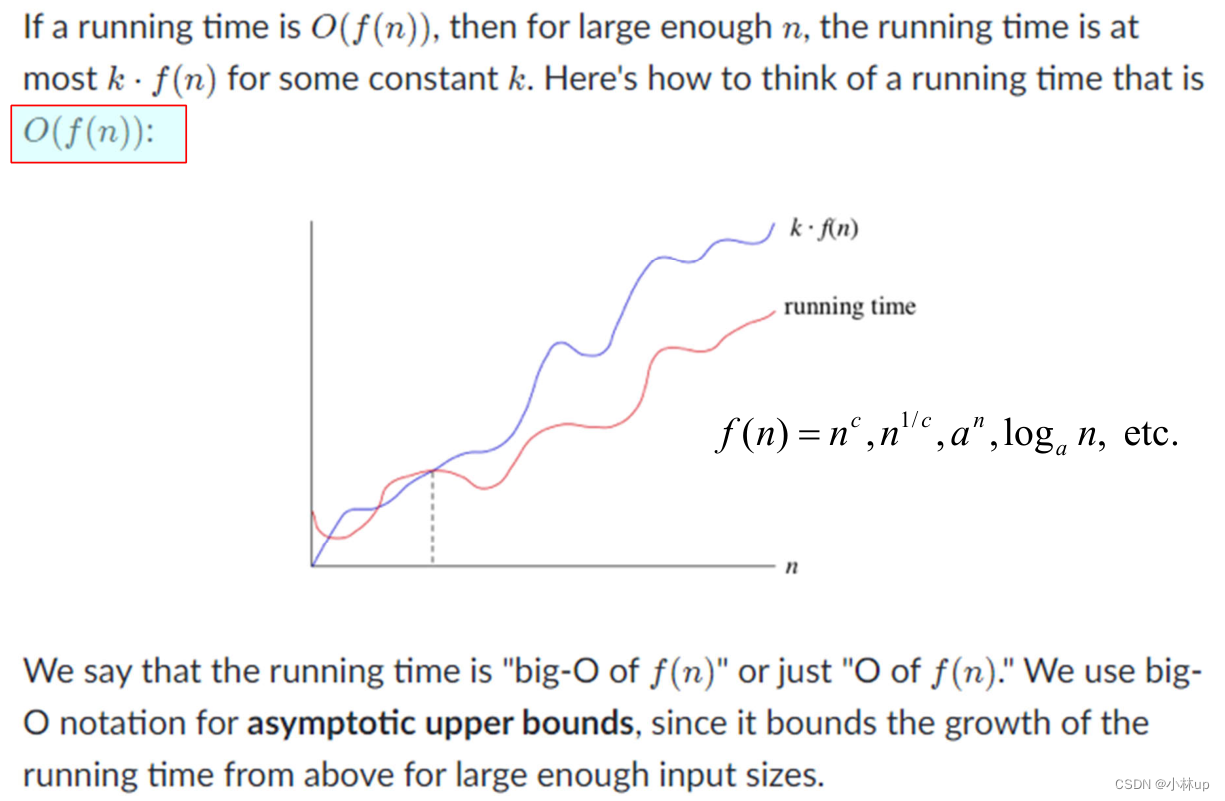

大Θ的记号:
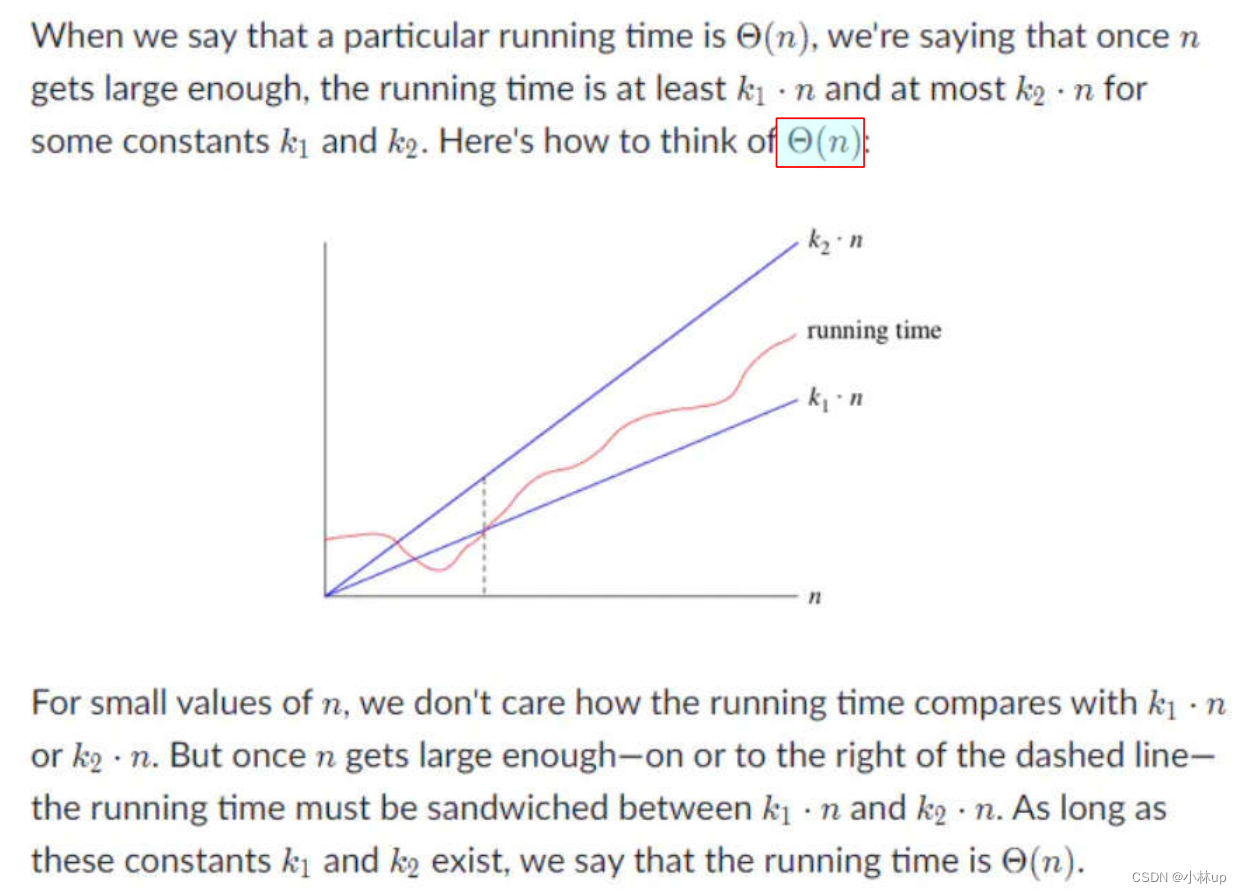
大Ω记号:
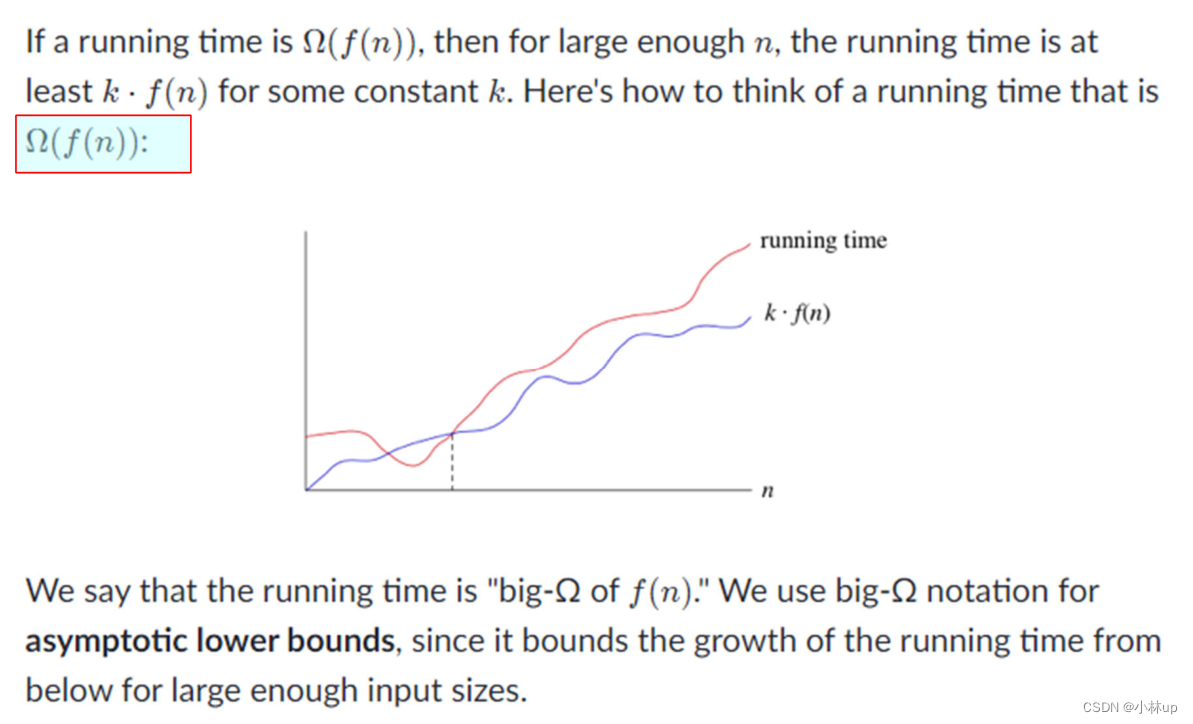
近似阶:

我们有四则运算法则:

3 误差传播与稳定性
四则运算的误差传递:
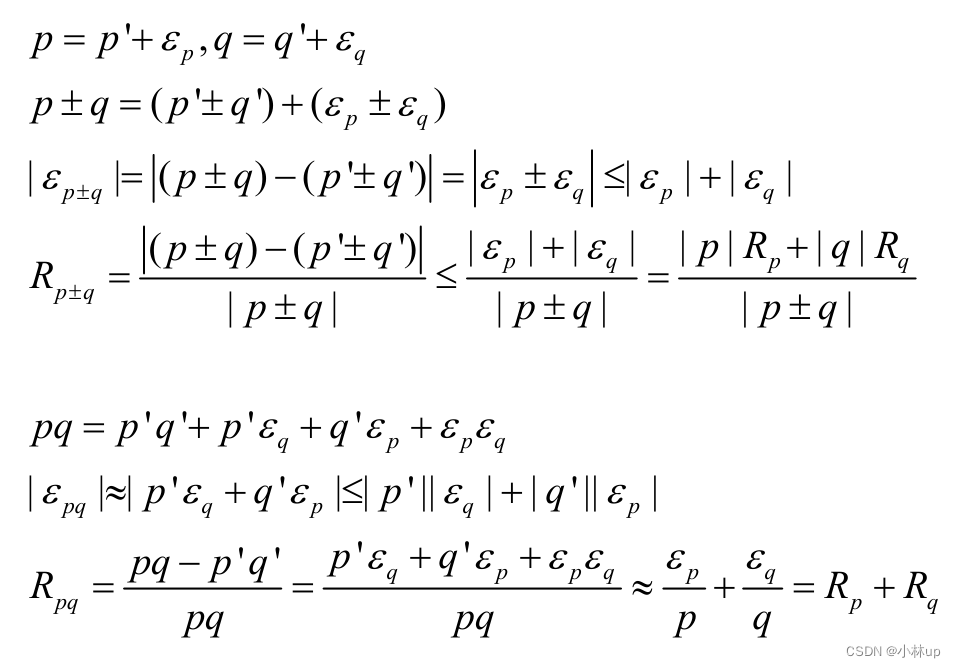
稳定和不稳定性
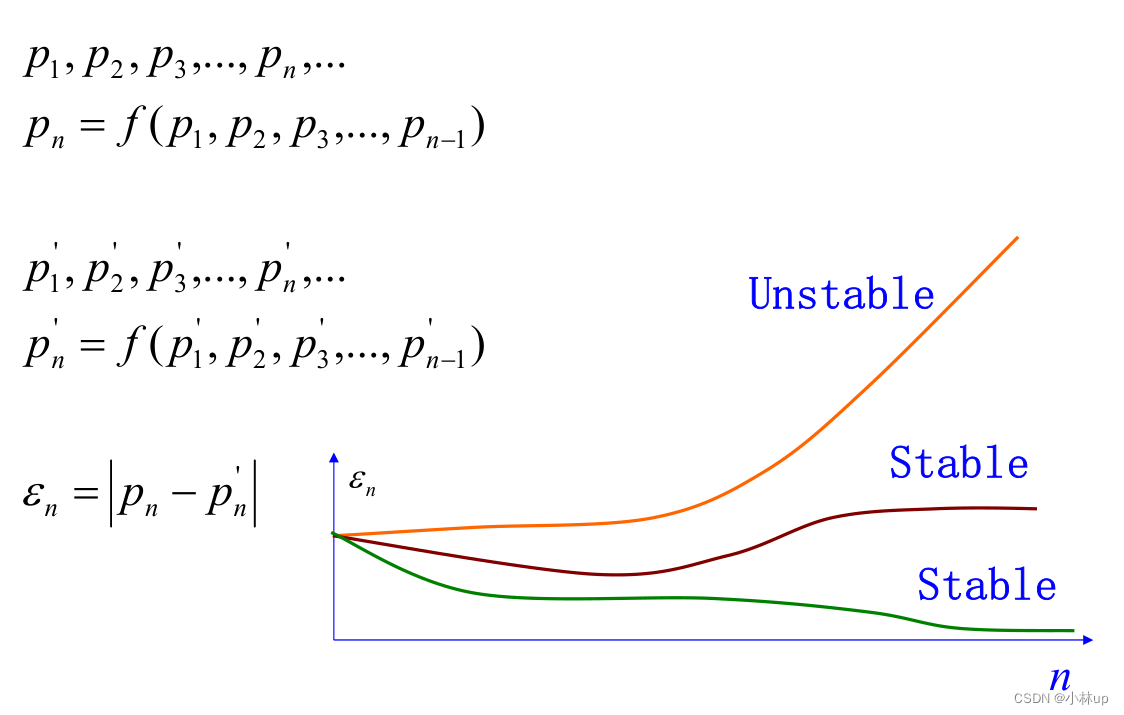
误差的增长,线性和指数
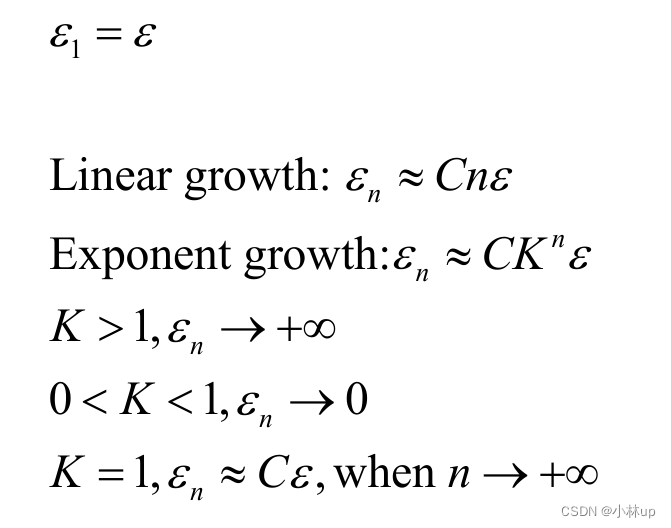


![buu [NPUCTF2020]Classical Cipher 1](https://img-blog.csdnimg.cn/3b5c07fe882942389f81a3ce512be516.png)