原题链接

难度：$middle$

---

题目描述

你会得到一个双链表，其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表，也包含这些特殊的节点。这些子列表可以有一个或多个自己的子列表，以此类推，以生成如下面的示例所示的 多层数据结构 。

给定链表的头节点 head ，将链表 扁平化 ，以便所有节点都出现在单层双链表中。让 $curr$ 是一个带有子列表的节点。子列表中的节点应该出现在 扁平化列表 中的 $curr$ 之后 和 $curr.next$ 之前 。

返回 扁平列表的 $head$ 。列表中的节点必须将其 所有 子指针设置为 $null$ 。

示例 1：

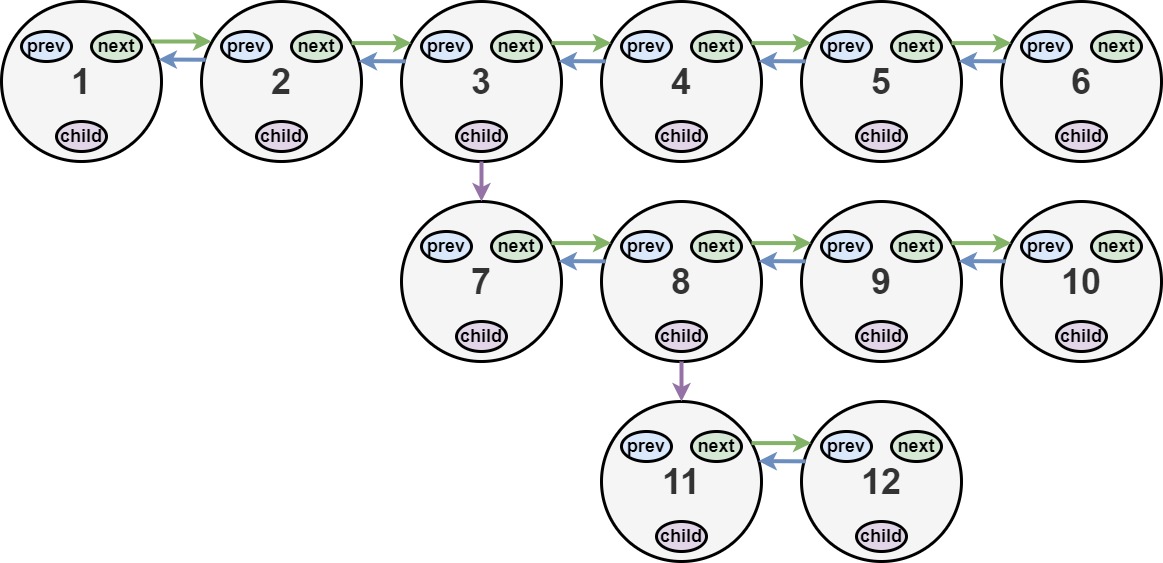
输入：head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
输出：[1,2,3,7,8,11,12,9,10,4,5,6]
解释：输入的多级列表如上图所示。
扁平化后的链表如下图：

示例 2：

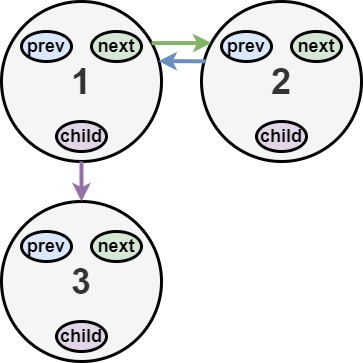
输入：head = [1,2,null,3]
输出：[1,3,2]
解释：输入的多级列表如上图所示。
扁平化后的链表如下图：

示例 3：

输入：head = []
输出：[]
说明：输入中可能存在空列表。

提示：

• 节点数目不超过 $1000$
• $1<=Node.val<=10^5$

如何表示测试用例中的多级链表？

以 示例 1 为例：

1---2---3---4---5---6--NULL
         |
         7---8---9---10--NULL
             |
             11--12--NULL

序列化其中的每一级之后：

[1,2,3,4,5,6,null]
[7,8,9,10,null]
[11,12,null]

为了将每一级都序列化到一起，我们需要每一级中添加值为 null 的元素，以表示没有节点连接到上一级的上级节点。

[1,2,3,4,5,6,null]
[null,null,7,8,9,10,null]
[null,11,12,null]

合并所有序列化结果，并去除末尾的 null 。

[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]

---

算法

(递归) $O(n)$

1. 定义 flat 函数，参数为当前级链表的头结点，返回当前级链表扁平化后的最后一个结点。
2. 在 flat 函数中，从头结点开始遍历，遍历的节点可分为四类：

   • 第一类：既没有孩子节点也没有后驱节点，说明说明已经是该层最后一个节点了，直接返回该节点。

   • 第二类：没有孩子节点，只有后驱节点。更新 head，让 head = head->next。

   • 第三类：既有孩子节点也有后驱节点：

     • 则用临时变量 nxt 记录下当前结点的 child 和 next，然后递归调用 flat(head->child)，用临时变量 tail 记录调用的返回值。
     • 递归结束后，需要修改当前结点 cur 的 child 和 next，以及 child 结点的 prev。修改 tail 的 next。如果 nxt 不为空，则修改 nxt 的 prev 为 tail。
     • 最后移动当前结点 cur 为 head。

   • 第四类：只有孩子节点，没有后驱节点。那么只需要将孩子节点变成后驱节点就可以了

复杂度分析

• 时间复杂度：每个结点仅遍历一次，故时间复杂度为 $O(n)$。

• 空间复杂度 : 递归需要系统栈空间，故空间复杂度为链表的最大级数。

C++ 代码

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
public:
    // flat 函数返回当前级链表扁平化后的最后一个结点
    Node* flat(Node* head) {
        while (head) {
            //既没有孩子节点也没有后驱节点，说明已经是该层最后一个节点了，如6,10,12。直接返回该节点
            if (!head->child && !head->next) return head;
            //如果没有孩子节点，只有后驱节点。如1，2，4，5，7，9，11，更新head
            else if (!head->child) head = head->next;
            //既有孩子节点也有后驱节点
            else if (head->next) {
                //先将孩子链表扁平化并返回末尾节点。
                Node* tail = flat(head->child);
                Node* nxt = head->next;

                tail->next = nxt;
                head->next = head->child;
                //将扁平化的链表插入当前节点的后面，注意是双向链表，并且孩子节点需要变成NULL
                if (tail->next) tail->next->prev = tail;
                if (head->next) head->next->prev = head;
                

                head->child = NULL;
                //更新当前节点
                head = tail->next;
            } else {
                //只有孩子节点，没有后驱节点。那么只需要将孩子节点变成后驱节点就可以了
                head->next = head->child;
                head->next->prev = head;
                head->child = NULL;
                head = head->next;
            }
        }
        return head;
    }
    

    Node* flatten(Node* head) {
        flat(head);
        return head;
    }
};