卷积神经网络（LeNet）

LeNet 的简化版

深层卷积神经网络（AlexNet）

从LeNet（左）到AlexNet（右）

改进：

1. dropOut层 - 不改变期望但是改变方差
2. ReLU层 - 减缓梯度消失
3. MaxPooling
4. 数据集数据增强

使用块的网络（VGG）

从AlexNet到VGG，它们本质上都是块设计。

网络中的网络（NiN)

对比 VGG 和 NiN 及它们的块之间主要架构差异

减少参数

含并行连结的网络（GoogLeNet）

Inception块的架构 GoogLeNet架构

	参数（M）	浮点运算（MFlops）
inception	0.16	128
3 * 3 Conv	0.44	346
5 * 5 Conv	1.22	963

模型小 参数少 结构复杂（代码多）

V2 + BN -> V3 换卷积 -> V4 加入残差

批量规范化（BN）

$\mathrm{BN}(\mathbf{x})=\mathbf{\gamma }\odot \frac{\mathbf{x}-{\hat{\mathbf{\mu }}}_{\mathcal{B}}}{{\hat{\mathbf{\sigma }}}_{\mathcal{B}}}+\mathbf{\beta }.$

因此我们通常包含 拉伸参数（scale）$\mathbf{\gamma }$
和偏移参数（shift）$\mathbf{\beta }$，它们的形状与相同。

请注意，$\mathbf{\gamma }$和$\mathbf{\beta }$是需要与其他模型参数一起学习的参数。

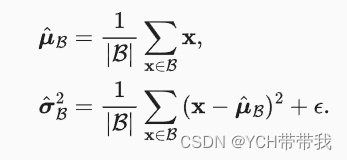
我们在方差估计值中添加一个小的常量$ϵ>0$
，以确保我们永远不会尝试除以零，即使在经验方差估计值可能消失的情况下也是如此。

估计值${\hat{\mathbf{\mu }}}_{\mathcal{B}}$和${\hat{\mathbf{\sigma }}}_{\mathcal{B}}$
通过使用平均值和方差的噪声（noise）估计来抵消缩放问题。 乍看起来，这种噪声是一个问题，而事实上它是有益的。

出现背景：backward时深层训练较快（深层语义），而浅层收敛慢（简单纹理）

思想：让每一层尽量服从同一分布，线性变换，使模型比较稳定

	作用	作用在
全连接	特征维	激活函数前	mean = X.mean(axis=0)
卷积层	通道维	激活函数前	mean = X.mean(axis=(0, 2, 3), keepdims=True)

只能加速收敛不能够增强精度

预测过程中的批量规范化

残差网络（ResNet）

对于非嵌套函数类，较复杂（由较大区域表示）的函数类不能保证更接近“真”函数（$f^*$）。这种现象在嵌套函数类中不会发生。 一个正常块（左图）和一个残差块（右图） 防止网络退化 包含以及不包含1 * 1卷积层的残差块。

稠密连接网络（DenseNet）Dense-全连接

泰勒公式 $f(x)=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\frac{f^{\prime \prime \prime }(0)}{3!}{x}^3+\dots .$

ResNet$f(\mathbf{x})=\mathbf{x}+g(\mathbf{x}).$

ResNet（左）与 DenseNet（右）在跨层连接上的主要区别：使用相加和使用连结

$\mathbf{x}\to \left[\mathbf{x},f_1(\mathbf{x}),f_2([\mathbf{x},f_1(\mathbf{x})]),f_3([\mathbf{x},f_1(\mathbf{x}),f_2([\mathbf{x},f_1(\mathbf{x})])]),\dots \right].$

稠密连接