摘要

剑指 Offer 39. 数组中出现次数超过一半的数字

一、摩尔投票法

核心理念票数正负抵消。此方法时间和空间复杂度分别为 O(N)和 O(1) ，为本题的最佳解法。

摩尔投票法：设输入数组 nums 的众数为 x ，数组长度为 n 。

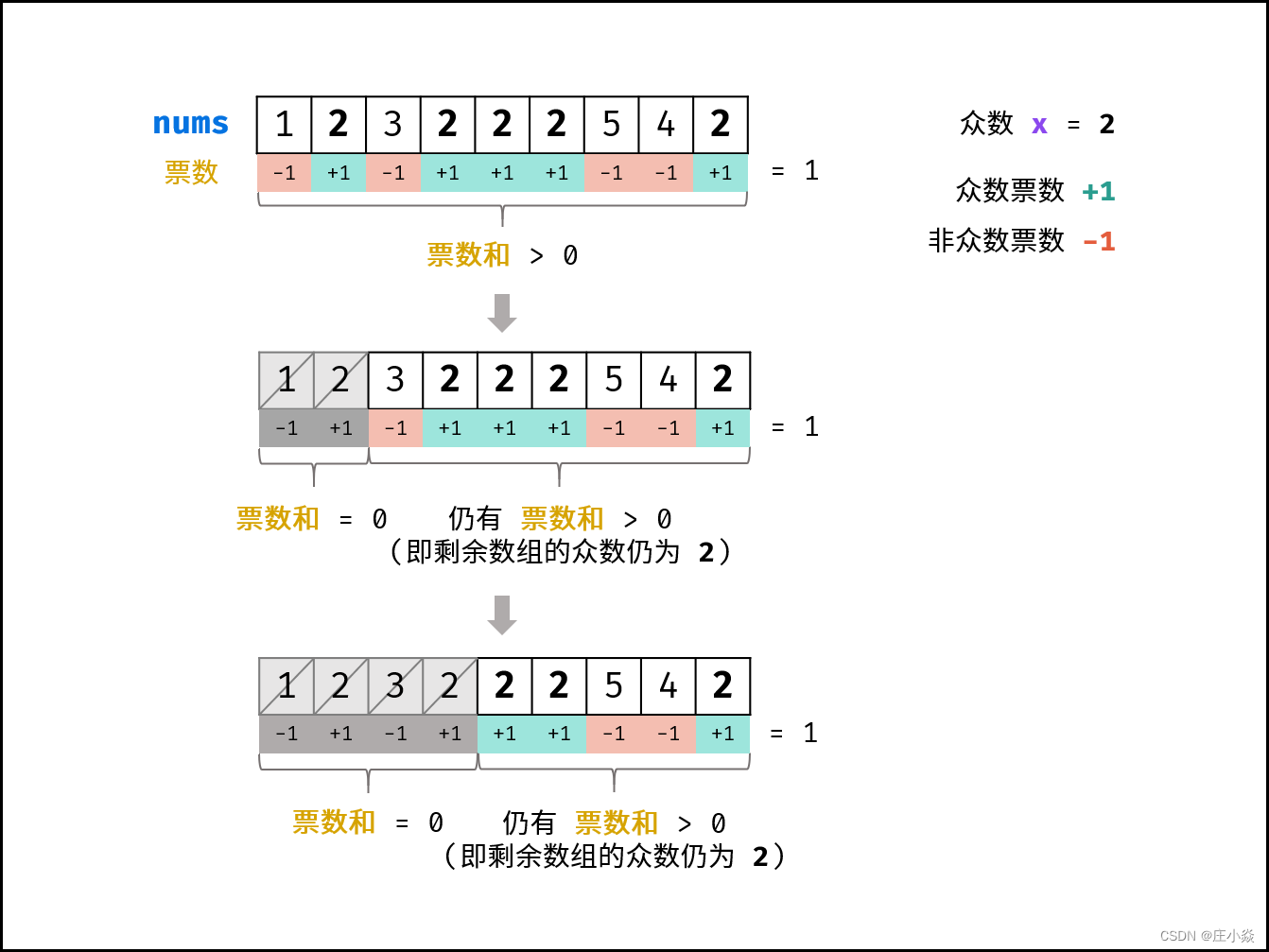
若记众数的票数为 +1 ，非众数的票数为 −1 ，则一定有所有数字的票数和 >0。
若数组的前 a个数字的票数和 =0，则数组剩余 (n−a)个数字的票数和一定仍>0 ，即后 (n−a)个数字的众数仍为 x 。

算法流程:

初始化：票数统计 votes = 0 ，众数 x；
循环：遍历数组 nums 中的每个数字 num ；
当票数 votes 等于 0 ，则假设当前数字 num 是众数；
当 num = x 时，票数 votes 自增 1 ；当 num != x 时，票数 votes 自减 1 ；
返回值：返回 x 即可；

class Solution {
    public int majorityElement(int[] nums) {
        int x = 0, votes = 0;
        for(int num : nums){
            if(votes == 0){
                x = num;
            }
            votes += num == x ? 1 : -1;
        }
        return x;
    }
}

复杂度分析：

时间复杂度 O(N) ： N为数组nums长度。
空间复杂度 O(1) ： votes 变量使用常数大小的额外空间

二、Hashmap解析

我们知道出现次数最多的元素大于n/2次，所以可以用哈希表来快速统计每个元素出现的次数。

我们使用哈希映射（HashMap）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后，我们遍历哈希映射中的所有键值对，返回值最大的键。我们同样也可以在遍历数组 nums 时候使用打擂台的方法，维护最大的值，这样省去了最后对哈希映射的遍历。

class Solution {
    private Map<Integer, Integer> countNums(int[] nums) {
        Map<Integer, Integer> counts = new HashMap<Integer, Integer>();
        for (int num : nums) {
            if (!counts.containsKey(num)) {
                counts.put(num, 1);
            } else {
                counts.put(num, counts.get(num) + 1);
            }
        }
        return counts;
    }

    public int majorityElement(int[] nums) {
        Map<Integer, Integer> counts = countNums(nums);

        Map.Entry<Integer, Integer> majorityEntry = null;
        for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
            if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()) {
                majorityEntry = entry;
            }
        }

        return majorityEntry.getKey();
    }
}

复杂度分析