1.股票买卖
一、贪心

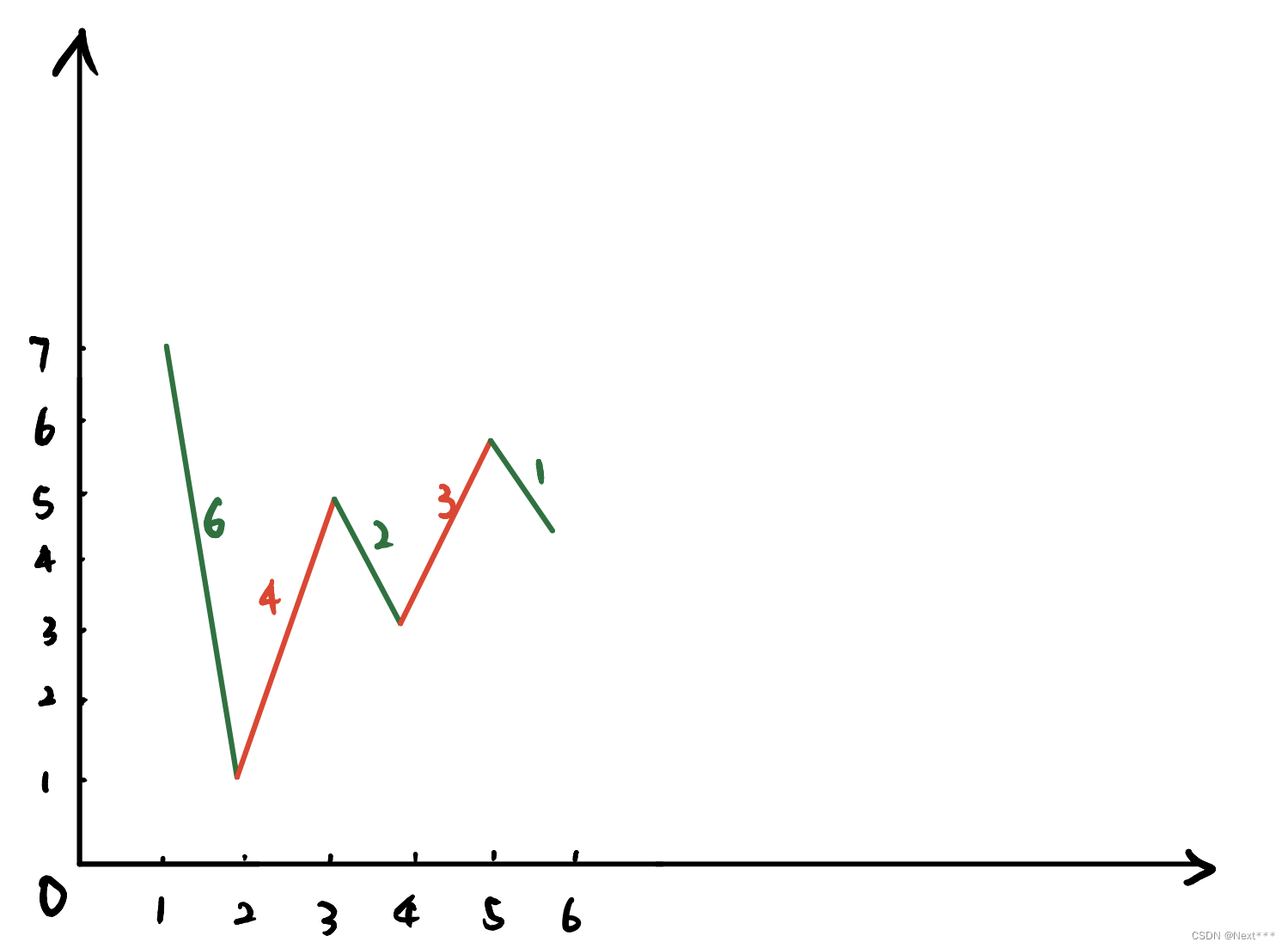
考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案
if (w[i] > w[i - 1])
res += w[i] - w[i - 1];
接下来证明该贪心思路得出的方案即是最优解。
(1)证明贪心解 ≥ 最优解:
由于贪心解都是取区间长度为 1 的解,因此假设存在于最优解中的某个区间 [i,j] 的长度 >1
那么会出现一下三种情况:
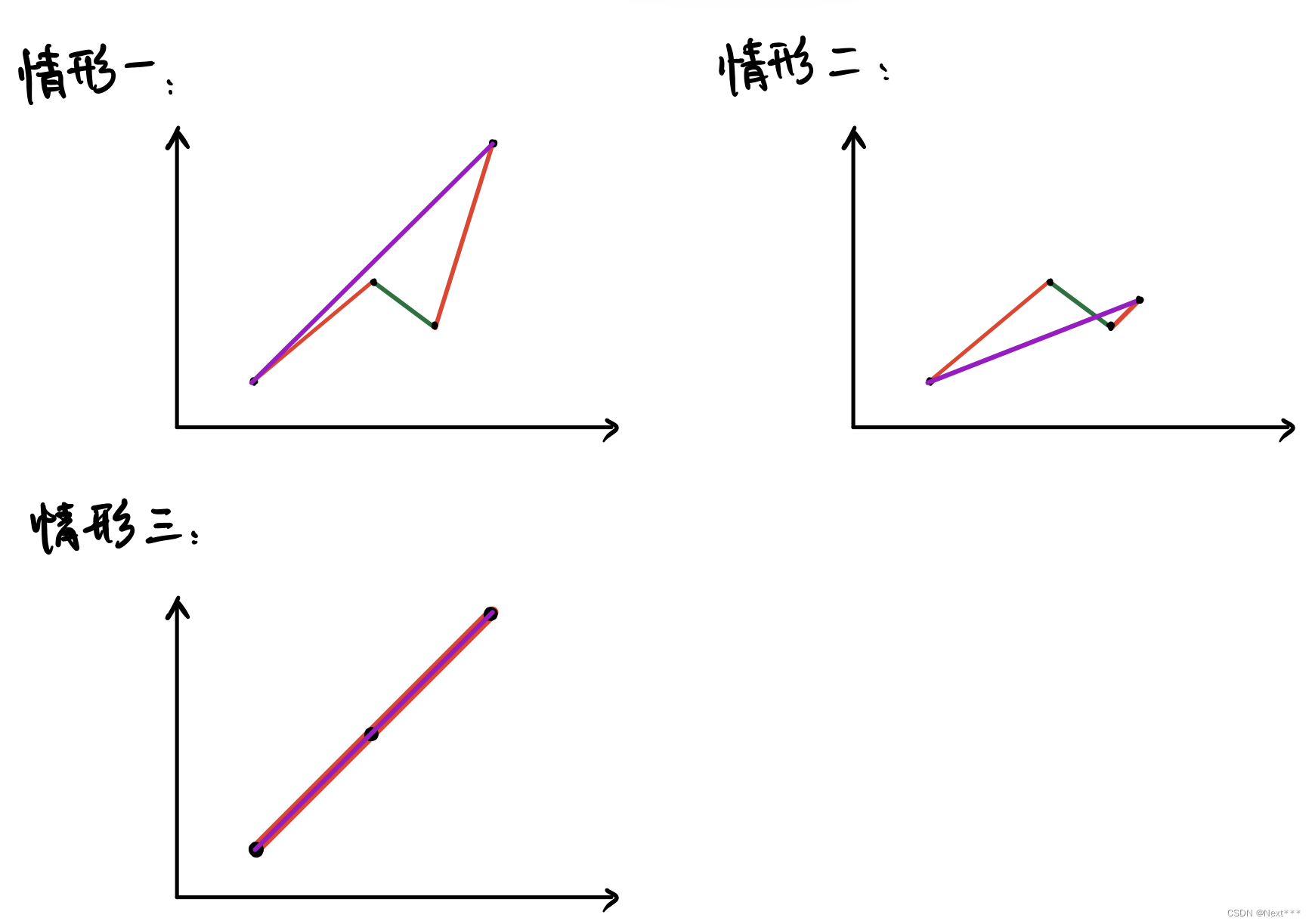
对应三种情形:最优解选取的区间最终点位于上方、下方、相等。
对于情形一:显然 最优解 < 贪心解
对于情形二:显然 最优解 <贪心解
对于情形三:毫无疑问,这就是存在于贪心解中的情形,因此 贪心解 = 最优解
得证
(2)证明贪心解 ≤最优解:
这部分无需证明,因为贪心解即是合法解,所以他的方案必定大于等于最优解
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int w[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
int res = 0;
for (int i = 2; i <= n + 1; ++i) {
if (w[i] - w[i - 1] > 0) res += w[i] - w[i - 1];
}
printf("%d\n", res);
return 0;
}
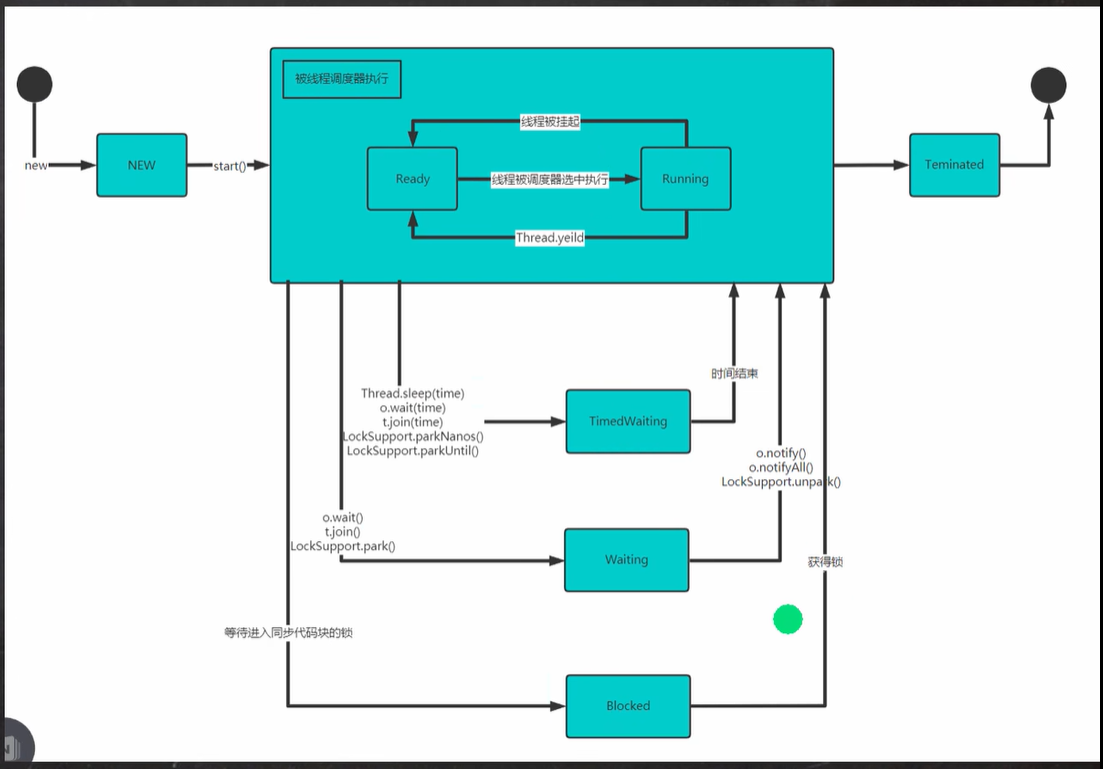
二、闫氏DP分析法
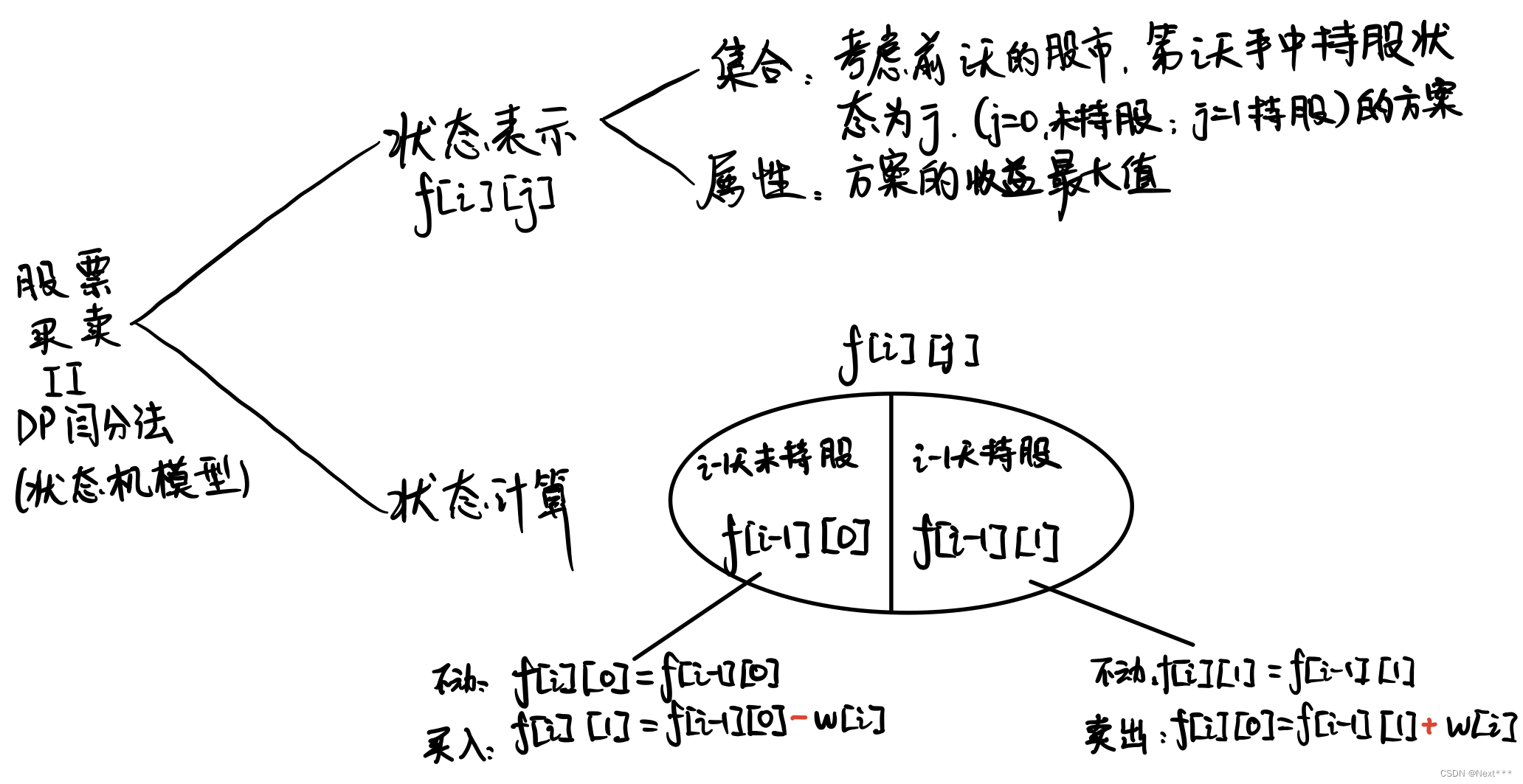
具体的状态机模型分析如下图:
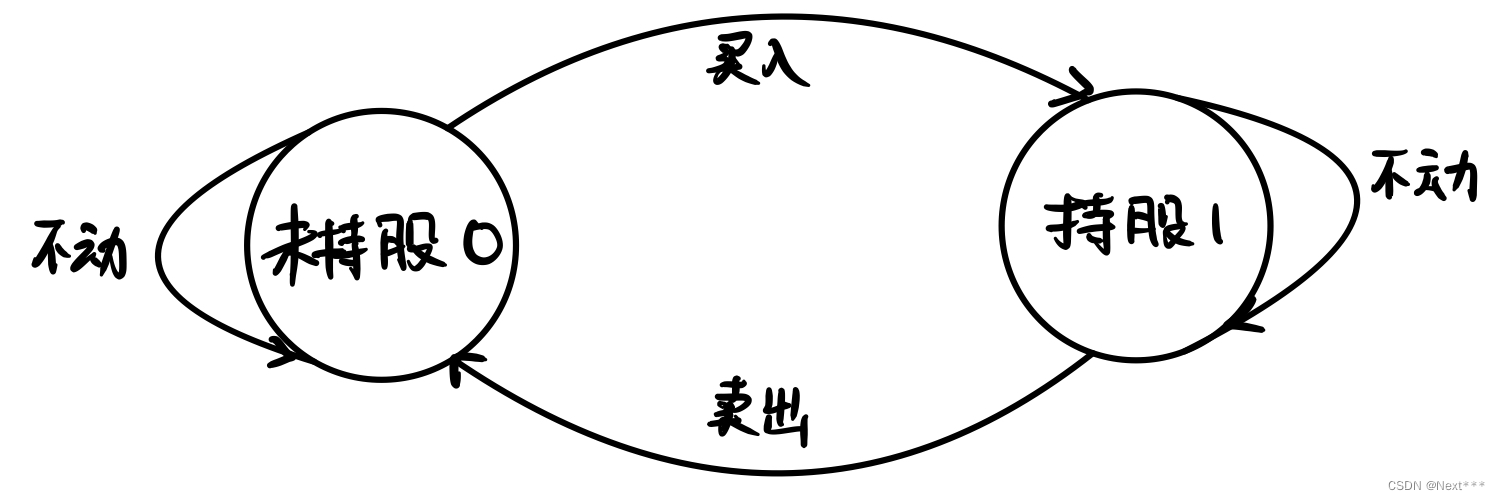
一共只2有种状态:
1. 当前处于未持股状态0:
对应可以进行的转换:
0->0 (不买入,继续观望,那么就什么都不发生)
0->1 (买入股票,那么收益就要减去当前市场的股票价格)
2. 当前处于持股状态1:
对应可以进行的转换:
1->1 (不卖出,继续观望,那么就什么都不发生)
1->0 (卖出股票,那么收益就要加上当前市场的股票价格)
#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][2];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
f[0][1] = -INF;
for (int i = 1; i <= n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
}
printf("%d\n", f[n][0]);
return 0;
}
2.货舱选址
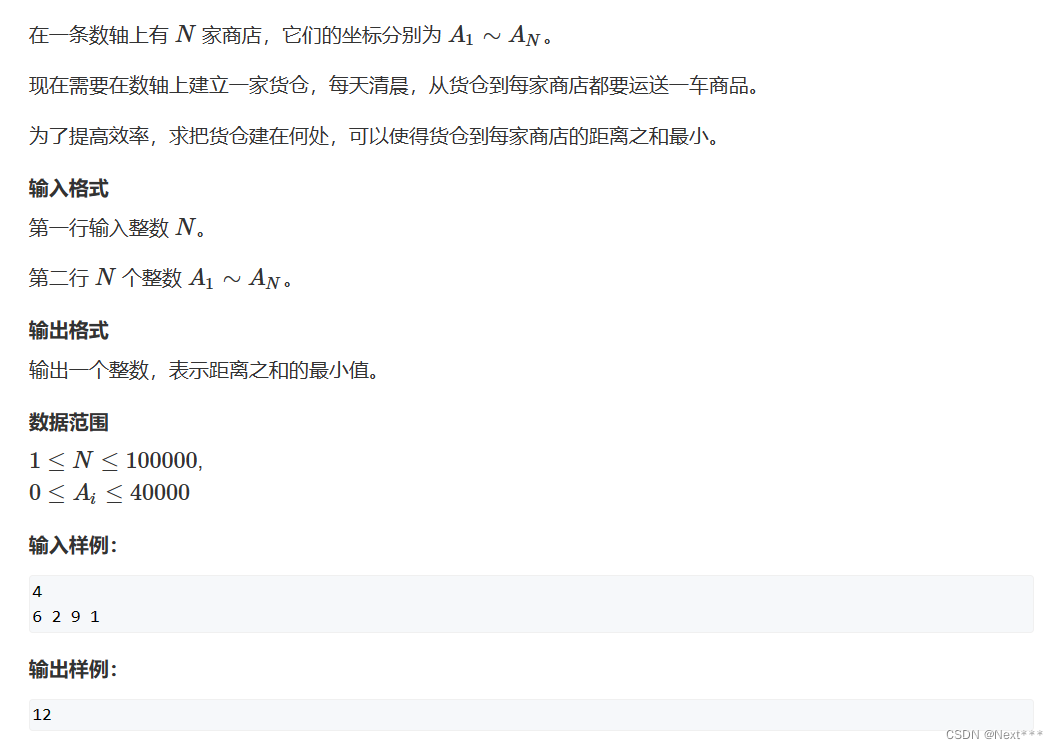
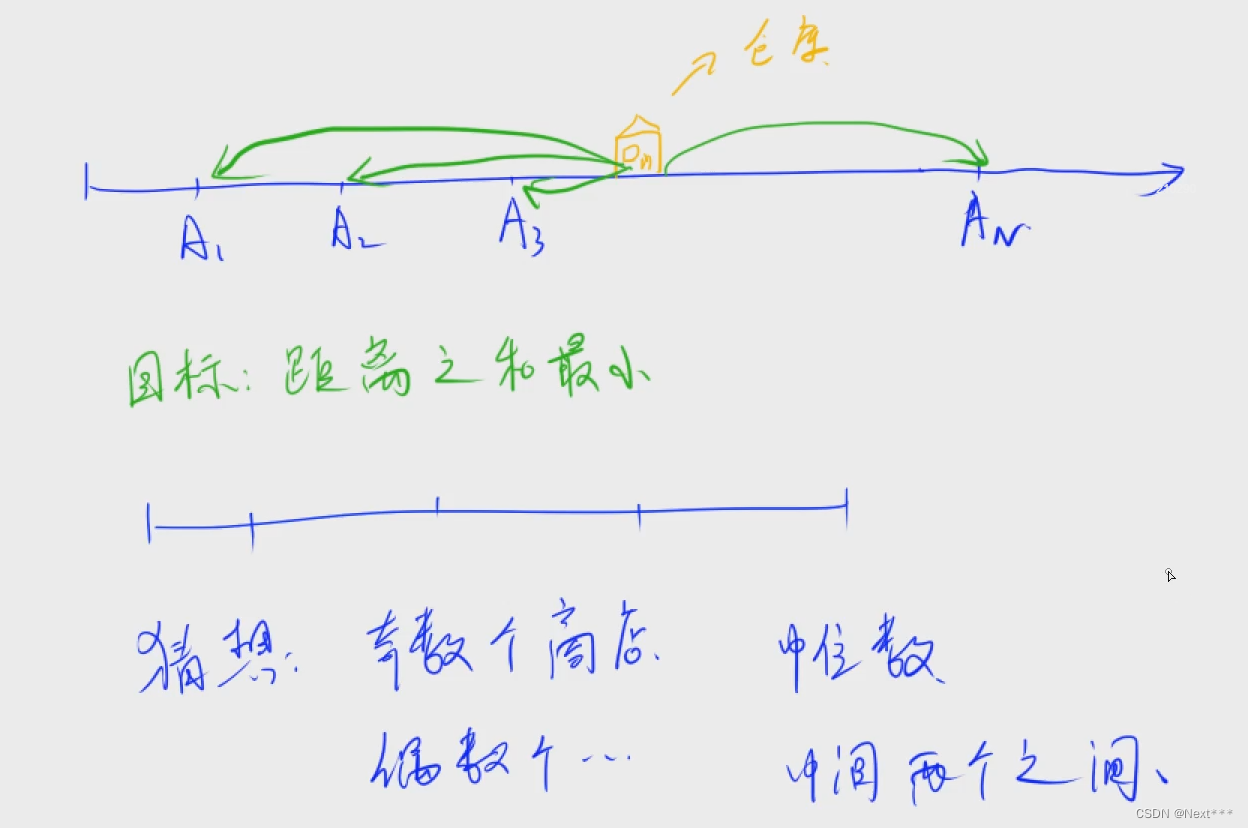

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {
scanf ("%d",&n);
for (int i = 1;i <= n;i++) scanf ("%d",&a[i]);
sort (a + 1,a + 1 + n);
int ans = 0;
for (int i = 1,j = n;i <= j;i++,j--) ans += a[j] - a[i];
printf ("%d\n",ans);
return 0;
}
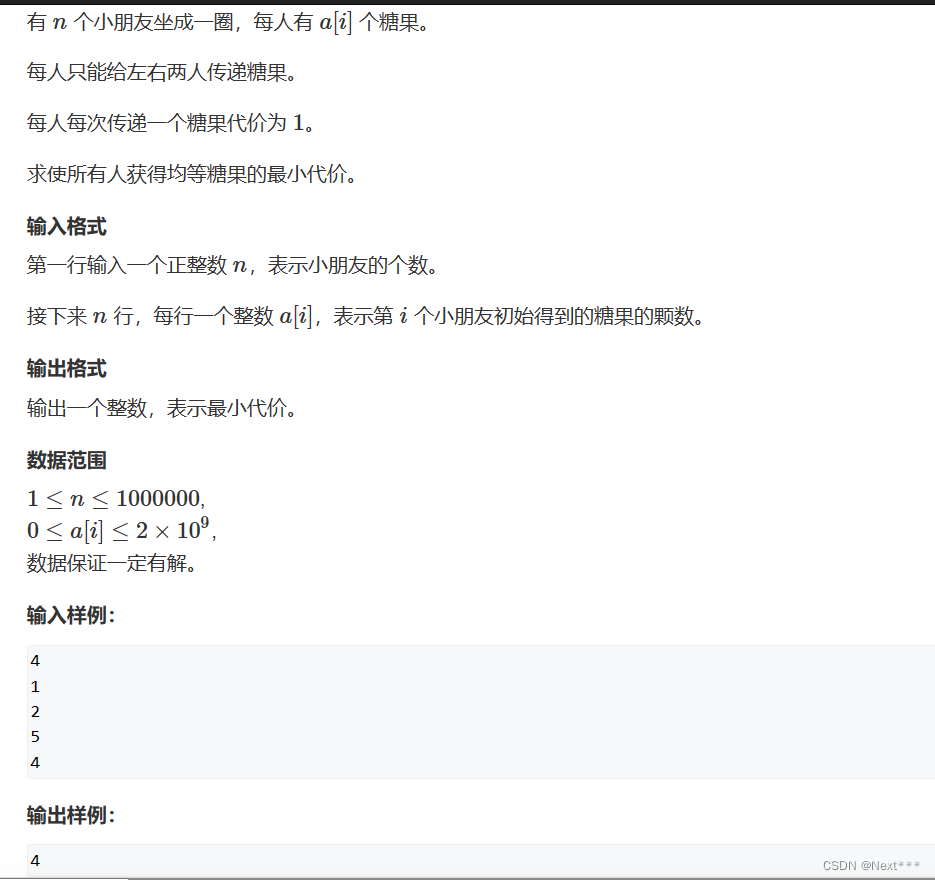
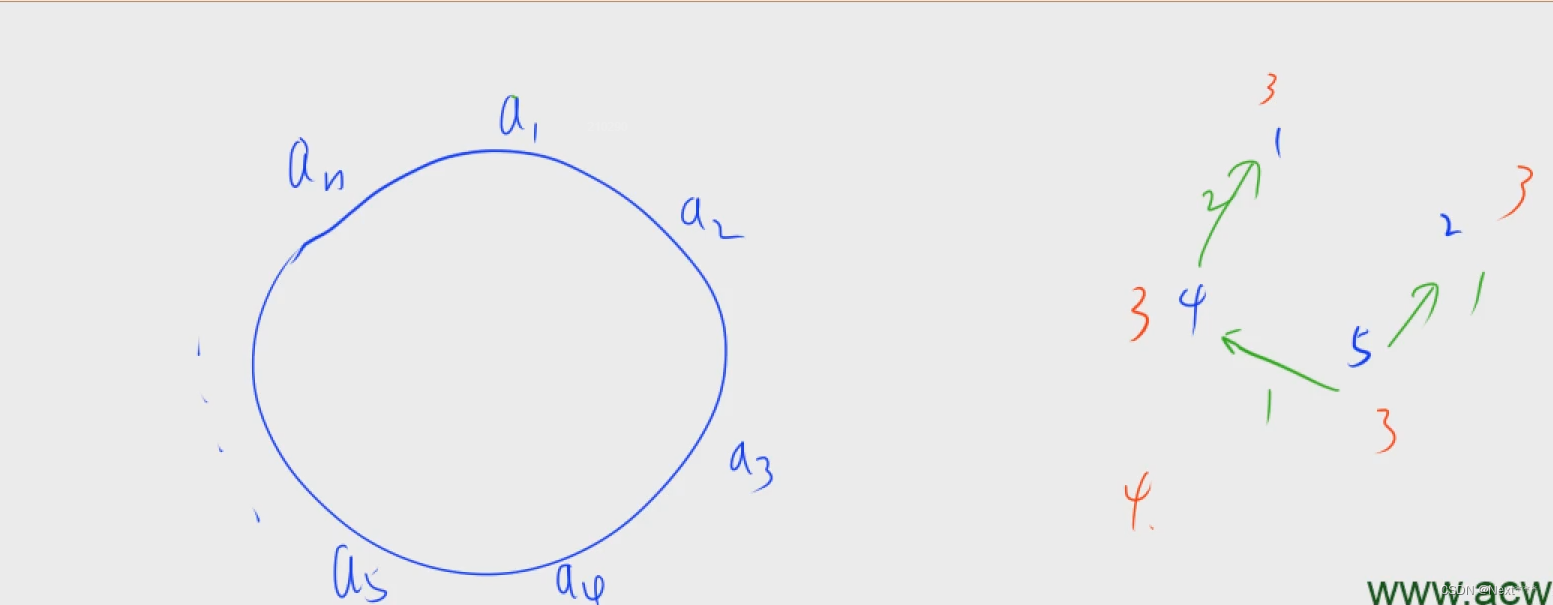
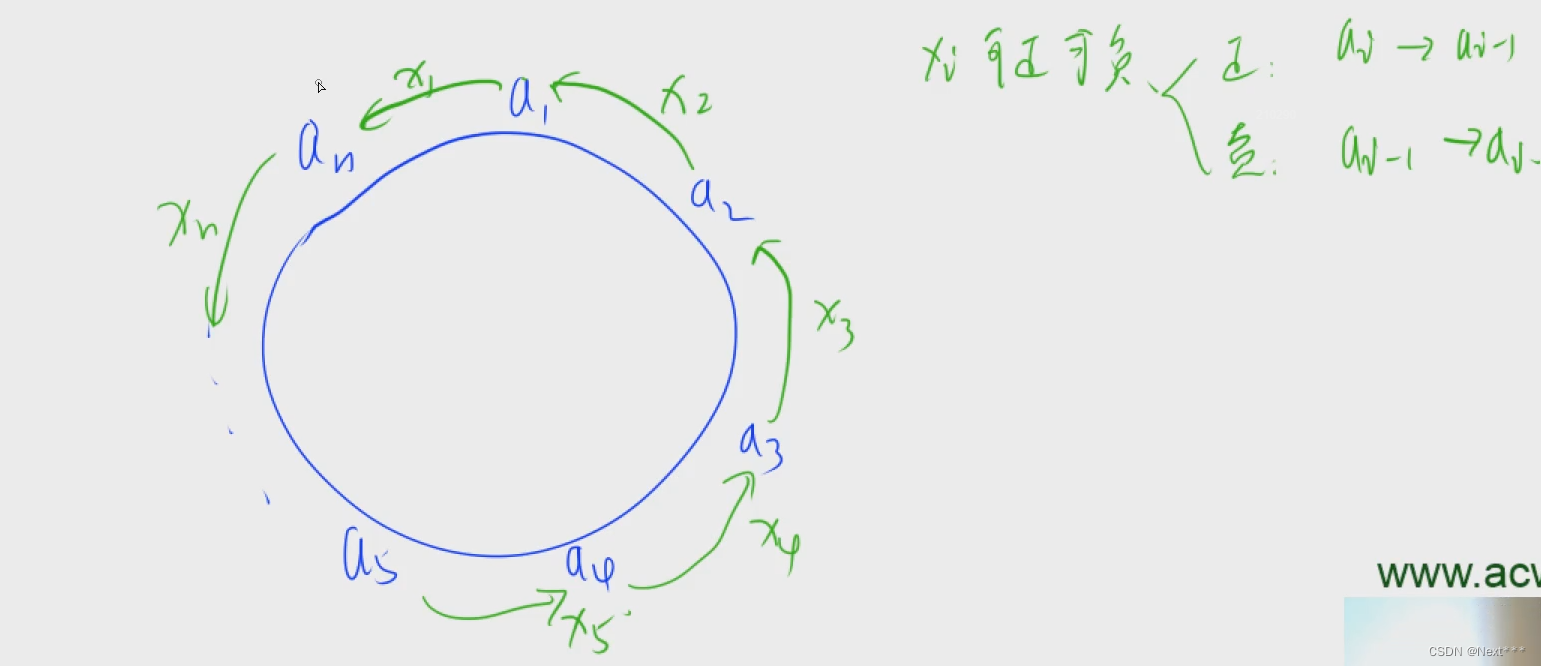
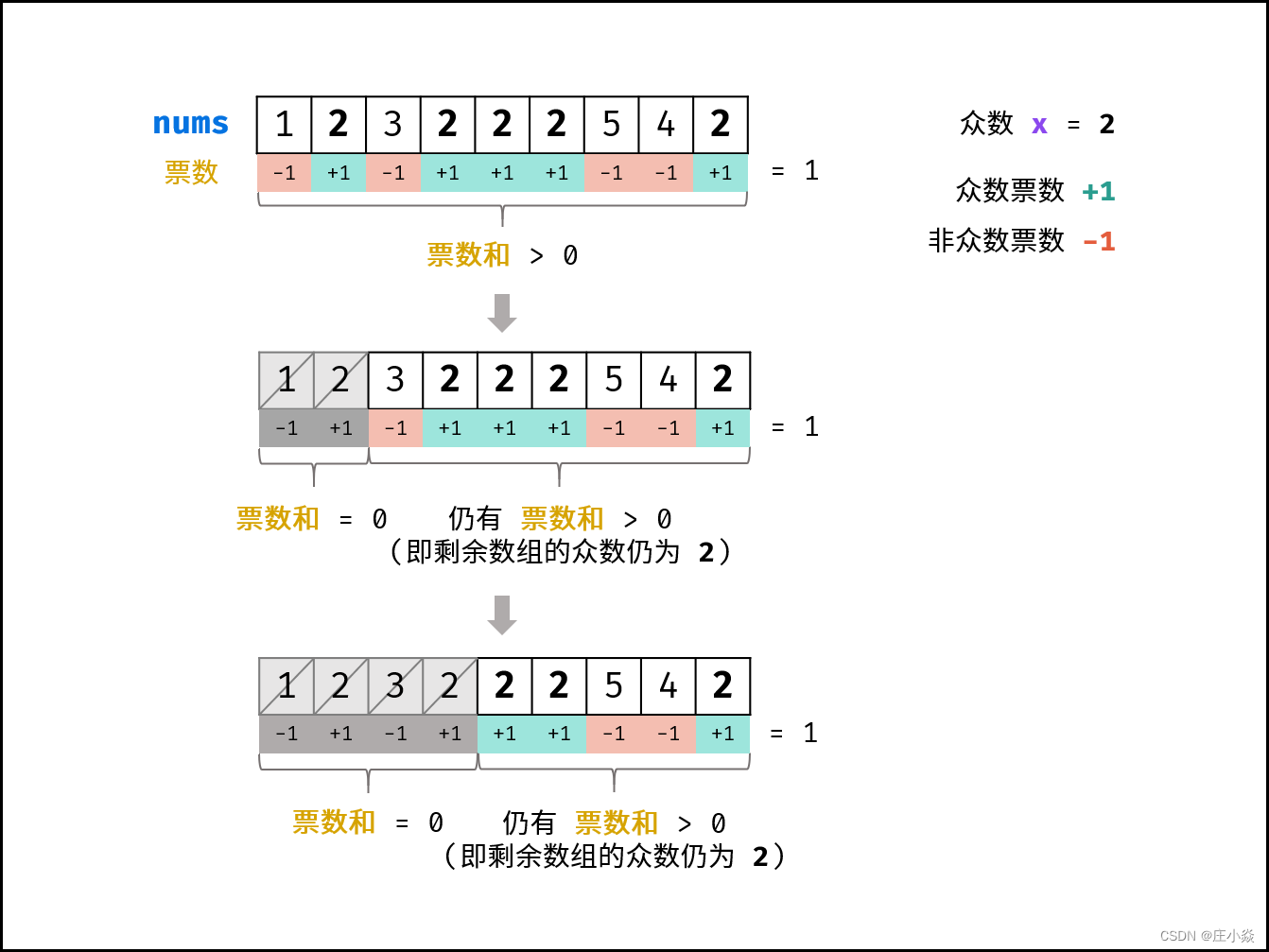
3.糖果传递