[acwing周赛复盘] 第 91 场周赛20230218
- 一、本周周赛总结
- 二、 4861. 构造数列
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、4862. 浇花
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、4863. 构造新矩阵
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- 这周挺难的。
- T1 贪心分解数位。
- T2 差分 / 排序模拟。
- T3 二分+思维。

二、 4861. 构造数列
链接: 4861. 构造数列
1. 题目描述
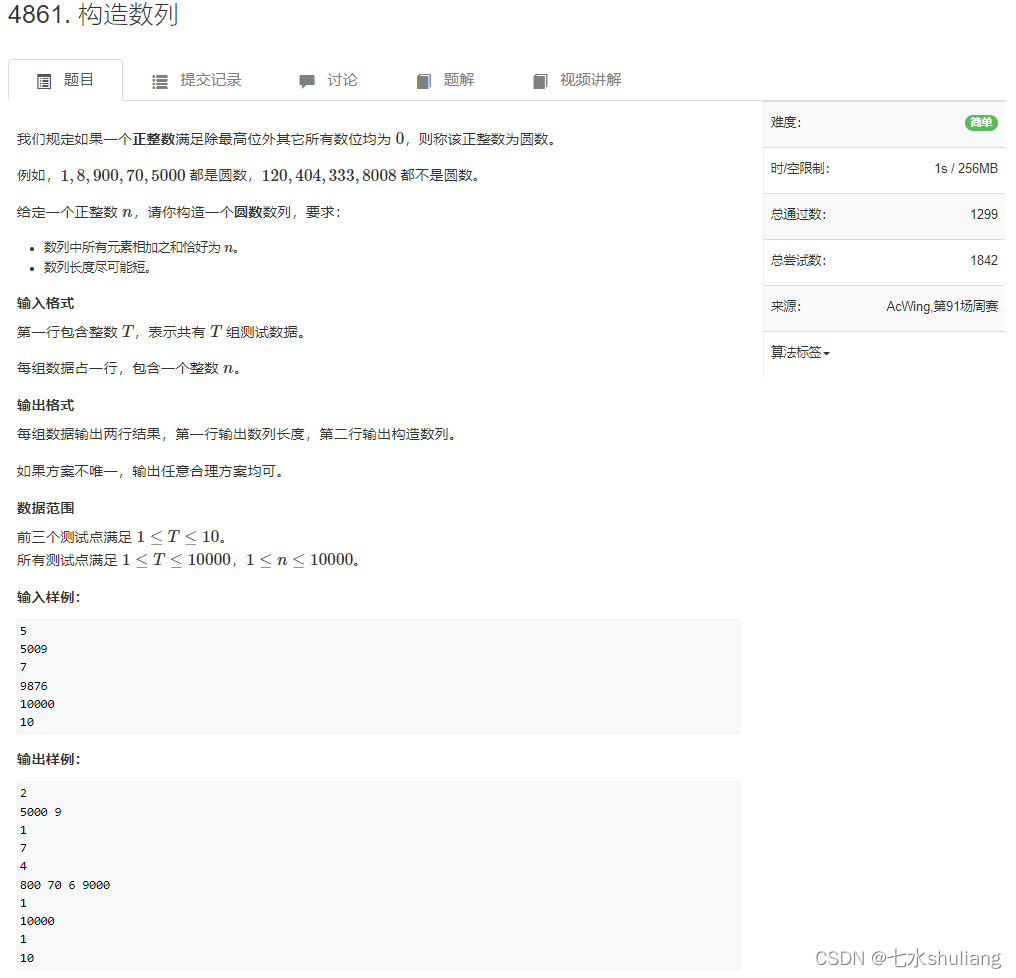
2. 思路分析
想了半天
- 其实就是贪心的处理每一位,拆出来即可。
3. 代码实现
# Problem: 构造数列
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4864/
# Memory Limit: 256 MB
# Time Limit: 1000 ms
import sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *
from math import sqrt, gcd, inf
if sys.version >= '3.8': # ACW没有comb
from math import comb
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
# ms
def solve():
n, = RI()
ans = []
base = 1
for i,v in enumerate(str(n)[::-1]):
if v != '0':
ans.append(int(v)*base)
base *= 10
print(len(ans))
print(*ans)
if __name__ == '__main__':
t, = RI()
for _ in range(t):
solve()
三、4862. 浇花
链接: 4862. 浇花
1. 题目描述
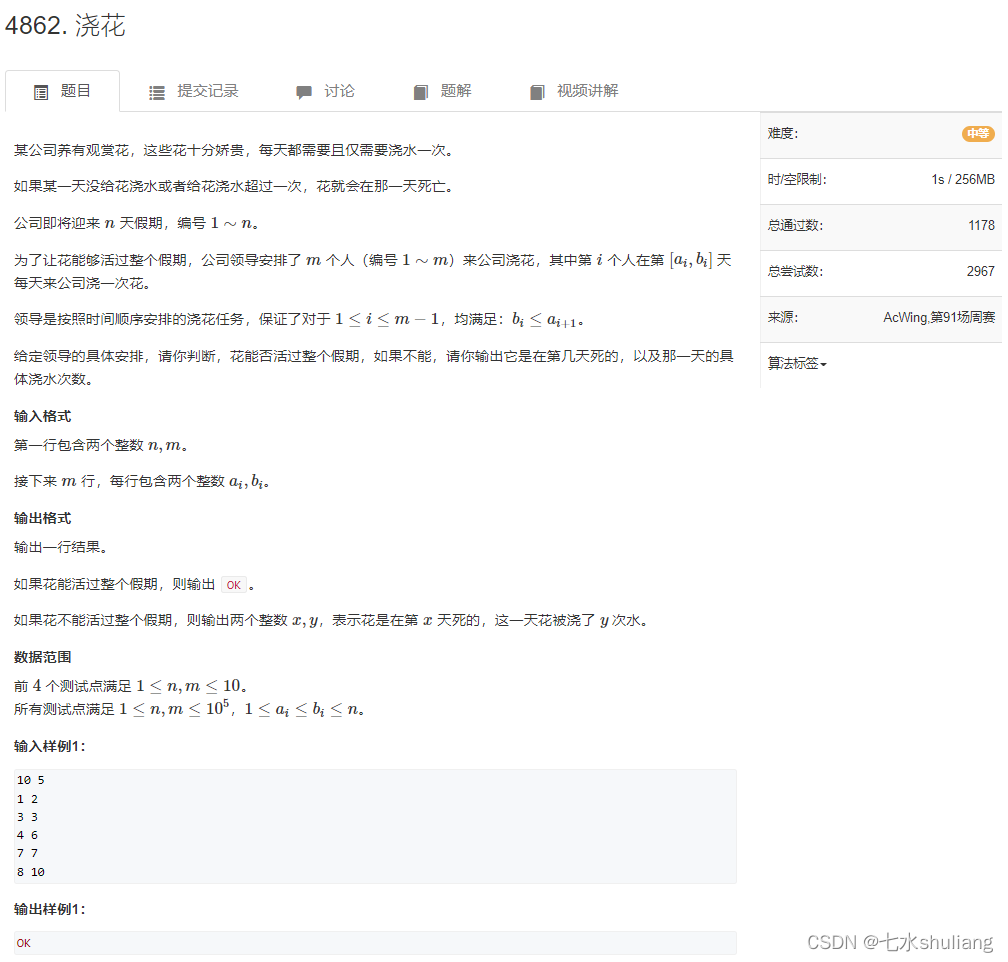
2. 思路分析
方法1,排序+模拟
- 由于数据是有序的,而且不允许重复,因此直接判断开始时间和上个元素的结束时间是否相邻即可。
- 数量就最后暴力。
方法2,差分
- 出题人的本意是让差分做,其实更好。
- 预处理差分数组后,遍历还原数组,应该每个值都是1,否则就返回失败。
3. 代码实现
# Problem: 浇花
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4865/
# Memory Limit: 256 MB
# Time Limit: 1000 ms
import sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *
from math import sqrt, gcd, inf
if sys.version >= '3.8': # ACW没有comb
from math import comb
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
# 差分 ms
def solve():
n, m = RI()
a = [0] * (n + 2)
for _ in range(m):
x, y = RI()
a[x] += 1
a[y + 1] -= 1
s = 0
for i in range(1,n+1):
s += a[i]
if s != 1:
return print(i,s)
print('OK')
# ms
def solve1():
n, m = RI()
a = []
for _ in range(m):
a.append(RILST())
a.sort()
i = 0
ans = -1
for x, y in a:
if x <= i:
ans = x
break
if x > i + 1:
ans = i + 1
break
i = y
else:
if i < n:
ans = i + 1
if ans == -1:
print('OK')
else:
s = sum(x <= ans <= y for x, y in a)
print(ans, s)
if __name__ == '__main__':
solve()
四、4863. 构造新矩阵
链接: 4863. 构造新矩阵
1. 题目描述

2. 思路分析
二分答案,但是judge函数需要一定思维。
- 考试时首交提交了个比较长的代码,复杂度看起来过不了,其实能过哈哈,已注释。
- 简单的方法:
- 判断每列都有满足>=L的数字,同时存在一行,有至少两个>=L的数字。
- 这是因为:只要每列(共n列)都有满足的数字,则起码可以选出n行来满足需求。
- 那么只要存在某行拥有2个>=L的数,就可以少取一行,变成n-1行。
- 其它情况则不满足。
- 然后二分即可:由于L越大越不可能满足,因此是单调递减的。
3. 代码实现
# Problem: 构造新矩阵
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4866/
# Memory Limit: 256 MB
# Time Limit: 1000 ms
import sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *
from math import sqrt, gcd, inf
if sys.version >= '3.8': # ACW没有comb
from math import comb
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
MOD = 10 ** 9 + 7
def my_bisect_left(a, x, lo=None, hi=None, key=None):
"""
由于3.10才能用key参数,因此自己实现一个。
:param a: 需要二分的数据
:param x: 查找的值
:param lo: 左边界
:param hi: 右边界(闭区间)
:param key: 数组a中的值会依次执行key方法,
:return: 第一个大于等于x的下标位置
"""
if not lo:
lo = 0
if not hi:
hi = len(a) - 1
else:
hi = min(hi, len(a) - 1)
size = hi - lo + 1
if not key:
key = lambda _x: _x
while size:
half = size >> 1
mid = lo + half
if key(a[mid]) < x:
lo = mid + 1
size = size - half - 1
else:
size = half
return lo
# 5148 ms
def solve():
RS()
m, n = RI()
g = []
for _ in range(m):
g.append(RILST())
# 首先判断若每列都有满足>=x的数,则起码可以选不超过n行出来,满足条件。
# 这是只要存在一行有用2个>=x得数,就可以少选一行即n-1行。
# 否则就不行
def ok(x):
if all(max(col) >= x for col in zip(*g)) and any(sum(v >= x for v in row) >= 2 for row in g):
return False
return True
print(my_bisect_left(range(10 ** 10), True, key=ok) - 1)
# 4887 ms
def solve1():
RS()
m, n = RI()
g = []
for _ in range(m):
g.append(RILST())
# 相当于给m个[1,0,1,0]布条重叠放,其中1是不透明的。
# 问最少几根布条叠在一起可以全部不透明。
# 或者说给m个n位的二进制数,问最少几个数或到一起可以全1。
# 贪心考虑,优先选1最多的那个数。
# 选了的1,从剩余数字每个中删掉,对剩余数字依然有1的数字,重新按照1数量排序。
# 直到选完了或者数字没有了。这时如果没选完就失败。
# 用set来储存每个数字1的位置,按len排序。每次排序复杂度log(m)
# 这里的复杂度看似很高,但其实每位上的1最多从每个数中删去1次,复杂度是m*n的。
def ok(x):
p = []
for row in g:
s = {i for i, v in enumerate(row) if v >= x}
if s:
p.append(s)
if not p:
return True
p.sort(key=len)
c = 0
t = set(range(n))
while t and p:
c += 1
if c > n - 1:
return True
s = p.pop()
if not s:
break
t -= s
q = []
for v in p:
v -= s
if v:
q.append(v)
p = q
p.sort(key=len)
if t:
return True
return False
print(my_bisect_left(range(10 ** 10), True, key=ok) - 1)
if __name__ == '__main__':
t, = RI()
for _ in range(t):
solve()
六、参考链接
- 无