zlib压缩原理

news2024/11/17 3:29:19

数据压缩的本质

去除数据中的冗余信息，对于ABABABABABABAB字样的字符串，AB出现了7次，占用14个字节，如果将该字符串编码为7AB，只占用3个字节。

为什么需要对数据压缩

数据需要存储或者传输，为了节省磁盘空间和网络带宽，在存储或传输时可以将数据先进行压缩，到真正需要使用数据的时候再进行解压。

zlib压缩

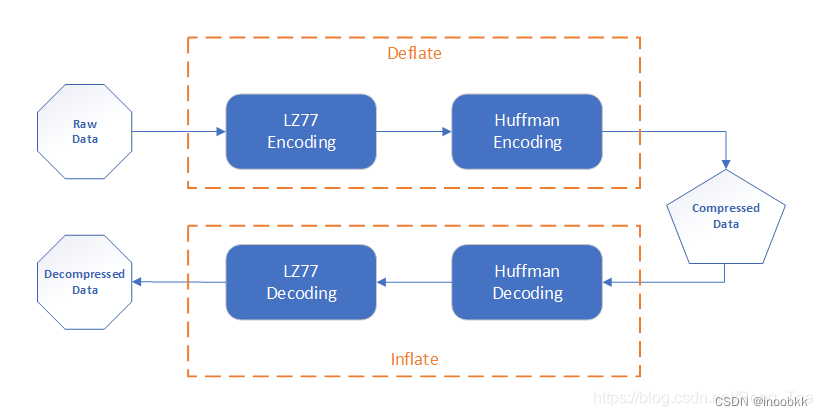
zlib压缩是一种无损压缩，底层使用deflate数据流压缩算法。

zlib压缩的特点：

无损压缩

压缩率取决于数据的重复性

deflate的三种压缩模型

不压缩数据。对于已经压缩过的数据，不再进行压缩。

压缩数据。先用LZ77进行压缩，再使用huffman编码。压缩树是deflate规定的。

压缩数据。先用LZ进行压缩，再使用huffman编码。压缩树是压缩其生成的

LZ77压缩算法

LZ77压缩算法的核心思想是对字符串进行扫描，对于前面已经出现过的子字符串，用（偏移量，匹配的字符串的长度）进行编码。LZ77中有三个重要的概念：短语字典、滑动窗口、前向缓冲区。

前向缓冲区：待编码的数据

滑动窗口：存放已经编码的数据

短语字典：用滑动窗口中的数据更新字典，并与前向缓冲区中的数据进行匹配

LZ77算法的步骤

步骤1：逐字符扫描前向缓冲区，在滑动窗口中找出匹配的最长子字符串，如果找到，则执行步骤2,如果没有找到，执行步骤3

步骤2：对前向缓冲区中匹配的字符串进行编码并输出，编码的格式为（前向缓冲区中匹配开始位置距离滑动窗口中匹配开始位置的偏移量，匹配的长度），将匹配的字符串移入滑动窗口中，继续执行步骤1

步骤3：将当前字符编码为（0,0,当前字符值）并输出，表示滑动窗口中没有出现过该字符，并将该字符移入到滑动窗口中，继续执行步骤1

例子

现在对ABABCBABABCAD这个字符串进行压缩。

滑动窗口大小为8,前向缓冲区大小为4。

开始，执行步骤1，将ABAB四个字符读入前向缓冲区，扫描到字符A，此时滑动窗口为空，没有找到匹配，执行步骤3, 将字符A编码为（0,0,A），并将字符A移入滑动窗口中，将C移入前向缓冲区。

继续执行步骤1，扫描到字符B，缓冲区中没有字符B，执行步骤3, 将字符B编码为（0,0,B），并将字符B移入滑动窗口中。

继续执行步骤1,扫描到字符A，滑动窗口中有字符A，继续扫描字符A后面的字符，当前字符串为AB，滑动窗口中有AB，继续向后扫描，得到字符串ABC，但滑动窗口中没有ABC，扫描结束，执行步骤2,将AB编码为（2,2），将AB移入滑动窗口

继续执行步骤1，扫描到字符C，缓冲区中没有字符C，执行步骤3, 将字符C编码为（0,0,C），并将字符C移入滑动窗口中

继续执行步骤1，匹配到BAB，执行步骤2, 将BAB编码为（4,3），移动缓冲区

继续执行步骤1，匹配到ABC，执行步骤2，将ABC编码为（6,3），移动缓冲区

继续执行步骤1，匹配到A，执行步骤2，将A编码为(5,1),移动缓冲区

继续执行步骤1，滑动窗口中没有字符D，执行步骤3,将D编码为（0,0,D），移动缓冲区

前向缓冲区为空，结束

最终的输出为：(0,0,A)，(0,0,B)，（2,2），(0,0,C)，(4,3)，(6,3)，(5,1)，(0,0,D)，可以按照这个序列进行解码

(0,0,A)->A

(0,0,B)->AB

(2,2)->ABAB

(0,0,C)->ABABC

(4,3)->ABABCBAB

(6,3)->ABABCBABABC

(5,1)->ABABCBABABCA

(0,0,D)->ABABCBABABCAD

Huffman编码

参考：https://blog.csdn.net/FX677588/article/details/70767446

哈夫曼（Huffman）编码算法是基于二叉树构建编码压缩结构的，它是数据压缩中经典的一种算法。算法根据文本字符出现的频率，重新对字符进行编码。我们希望出现频率越高的字符的编码后的长度越小。

重要的性质

哈夫曼编码是一种前缀编码。前缀编码指的是，任何一个字符的编码都不是同一字符集中另一个字符的编码的前缀。比如，将字符A编码为0,那么则不能将字符B编码为01。

这个性质对于解码起着重要的作用

构建哈夫曼二叉树

对于字符串“we will we will r u”，如果直接使用ASCII编码，编码后每个字符表示为（包括空格）：

119 101 32 119 105 108 108 32 119 101 32 119 105 108 108 32 114 32 117，可见需要19个字节存储这段信息，共152位。

现在对每个字符出现的频率进行统计，得到下表：

首先按照字符出现的频率从低到高的顺序对字符进行排序，存储到一个优先队列中，优先队列中每个元素可以看成一个节点，每个节点具有值和权重（出现的次数）两种属性

为了得到哈夫曼树，需要对优先队列进行从左到右进行合并，将u作为左节点，r作为右节点，将r和u的权重（出现的次数）相加，得到一个新的节点，作为u和r的父节点。

继续将这个新节点与节点i进行合并

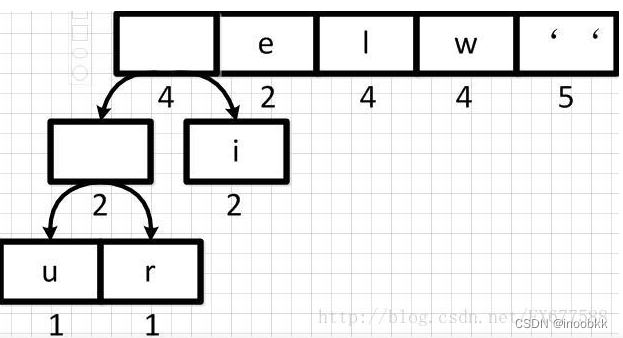
此时优先队列中的元素不再按照权重从低到高的顺序进行排列了，对优先队列进行重新排序

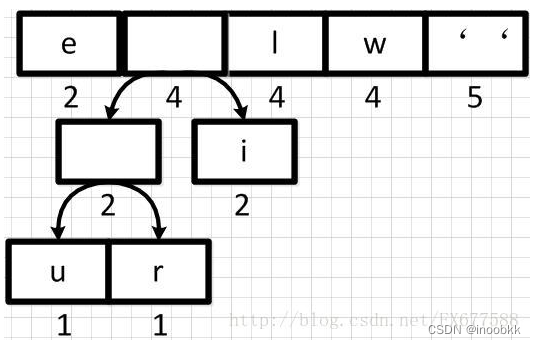
重复进行合并与排序操作，直到优先队列中只有一个根节点，最后得到huffman树

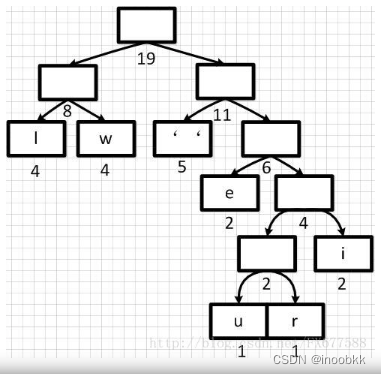
问一个问题：为什么要将元素按照出现次数从低到高排列

根据haffman树进行编码

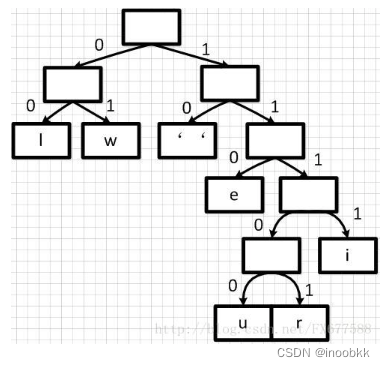
得到huffman树后，将该二叉树中分支中的左支路编码为0,右支路编码为1，得到编码二叉树

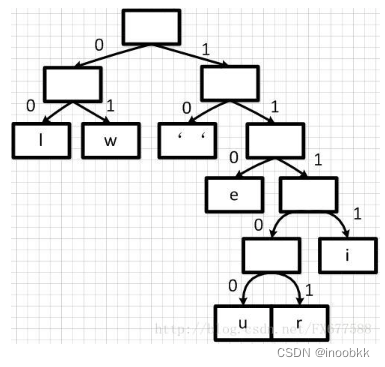
最后，根据编码二叉树得到每个字符的编码

空格：10

w：01

l：00

e：110

i：1111

r：11101

u：11100

可以看出，对于出现频率越高的字符，编码后的长度越小

字符串编码

有了上面的编码表之后，”we will we will r u”这句重新进行编码就可以得到很大的压缩，编码表示为：01 110 10 01 1111 00 00 10 01 110 10 01 1111 00 00 10 11101 10 11100。这样最终我们只需50位内存，比原ASCII码表示节约了2/3空间，效果还是很理想的。当然现实中不是简单这样表示的，还需要考虑很多问题。