决策树是一种非参数的监督学习方法，主要用于分类和回归。

决策树结构

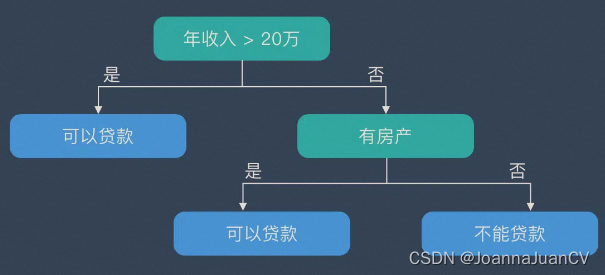
决策树在逻辑上以树的形式存在，包含根节点、内部结点和叶节点。

• 根节点：包含数据集中的所有数据的集合
• 内部节点：每个内部节点为一个判断条件，并且包含数据集中满足从根节点到该节点所有条件的数据的集合。根据内部结点的判断条件测试结果，内部节点对应的数据的集合别分到两个或多个子节点中。
• 叶节点：叶节点为最终的类别，被包含在该叶节点的数据属于该类别。

决策树学习的 3 个步骤

特征选择

在构建决策树的过程中，选择最佳（既能够快速分类，又能使决策树的深度最小）的分叉特征属性是关键所在。这种“最佳性”可以用非纯度进行衡量。如果一个数据集合中只有一种分类结果，则该集合最纯，即一致性好；反之，有许多分类，则不纯，即一致性不好。
一般的原则是，希望通过不断划分节点，使得一个分支节点包含的数据尽可能的属于同一个类别，即“纯度“越来越高。
常用的准则有：熵，基尼指数和分类误差， 公式分别为：

$$Entropy=E(D)=-\sum _{j=1}^J{p}_j{\log }_2{p}_j$$
$$GiniIndex=Gini(D)=\sum _{j=1}^J{p}_j(1-p_j)=\sum _{j=1}^J{p}_j-\sum _{j=1}^J{p}_j^2=1-\sum _{j=1}^J{p}_j^2$$

C l a s s i f i c a t i o n E r r o e = 1 − max ⁡ { p j } Classification Erroe = 1- \max{\{p_j\}} ClassificationErroe=1−max{pj​}

上述，所有公式中，值越大表示越不纯；式中，$D$表示样本数据的分类及和。设该集合共有$J$中分类，$p_j$表示第$j$种分类的样本率：
$$p_j=\frac{N_j}{N}$$
式中，$N$和$N_j$分辨表示集合$D$中样本数据的总数和第$j$个分类的样本数量。

决策树生成

选择好特征后，就从根节点触发，对节点计算所有特征的信息增益，选择信息增益最大的特征作为节点特征，根据该特征的不同取值建立子节点；对每个子节点使用相同的方式生成新的子节点，直到信息增益很小或者没有特征可以选择为止。

决策树剪枝

剪枝的主要目的是对抗「过拟合」，通过主动去掉部分分支来降低过拟合的风险。

决策树算法

ID3 算法
ID3 是最早提出的决策树算法，他就是利用信息增益来选择特征的。

C4.5 算法
他是 ID3 的改进版，他不是直接使用信息增益，而是引入“信息增益比”指标作为特征的选择依据。

CART（Classification and Regression Tree）
这种算法即可以用于分类，也可以用于回归问题。CART 算法使用了基尼系数取代了信息熵模型。

测试用例-评估是否发放贷款

#include<iostream>
#include<opencv2/highgui/highgui.hpp>
#include<opencv2/core/core.hpp>
#include<opencv2/imgproc/imgproc.hpp>
#include<opencv2/ml/ml.hpp>

using namespace std;
using namespace cv;
using namespace cv::ml;

static const char* var_desc[] = 
{
	"Age (young=Y, middle=M, old=O)",
	"Salary? (Low=L, medium=M, high=H)",
	"Own_House? (false=N, true=Y)",
	"Own_Car? (false=N, true=Y)",
	"Credit_Rating (fair=F, good=G, excellent=E",
	0
};

int main(int argc, char *argv[])
{
	//训练样本：年龄，薪水，房子，车，信贷情况
	float trainData[19][5] = { 
	{'Y','L','N','N','F'},
	{'Y','L','Y','N','G'},
	{'Y','M','Y','N','G'},
	{'Y','M','Y','Y','G'},
	{'Y','H','Y','Y','G'},
	{'Y','M','N','Y','G'},
	{'M','L','Y','Y','E'},
	{'M','H','Y','Y','G'},
	{'M','L','N','Y','G'},
	{'M','M','Y','Y','F'},
	{'M','H','Y','Y','E'},
	{'M','L','N','N','G'},
	{'O','L','N','N','G'},
	{'O','L','Y','Y','E'},
	{'O','L','Y','N','E'},
	{'O','M','N','Y','G'},
	{'O','L','N','N','E'},
	{'O','H','N','Y','F'},
	{'O','H','Y','Y','E'},
	};
	Mat trainDataMat(19, 5, CV_32FC1, trainData);
	//cout << trainDataMat << endl;
	//训练样本的响应值,1代表G  -1代表B    
	float labels[19] = { 'N' ,'N' ,'Y','Y','Y','N','Y','Y','N' ,'N','Y','N' ,'N' ,'Y','Y','N' ,'N' ,'N' ,'Y' };
	Mat labelsMat(19, 1, CV_32FC1, labels);
	//cout << labelsMat << endl;

	//建立模型
	Ptr<DTrees> model = DTrees::create();
	//树的最大可能深度
	model->setMaxDepth(8);
	//节点最小样本数量
	model->setMinSampleCount(2);
	//是否建立替代分裂点
	model->setUseSurrogates(false);
	//交叉验证次数
	model->setCVFolds(0);
	//是否严格修剪
	model->setUse1SERule(false);
	//分支是否完全移除
	model->setTruncatePrunedTree(false);
	//创建TrainData并进行训练
	Ptr<TrainData> tData = TrainData::create(trainDataMat, ROW_SAMPLE, labelsMat);
	model->train(tData);

	//保存决策树为xml文件
	const std::string save_file{ "decision_tree_model.xml" }; // .xml, .yaml, .jsons
	model->save(save_file);

	float myData[5] = { 'M','H','Y','N','F'};//测试样本
	Mat myDataMat(5, 1, CV_32FC1, myData);
	//利用训练好的分类器进行测试样本预测
	cv::Mat rMat;
	double r = model->predict(myDataMat, rMat, false);
	std::cout << "result: " << (char)r <<endl;

	//测试加载保存的决策树进行预测
	Ptr<DTrees> dtree = DTrees::load("decision_tree_model.xml");
	r = dtree->predict(myDataMat, rMat, false);
	std::cout << "result: " << (char)r << endl;

	return 0;
}

结果：

result: N
result: N