1 计算图

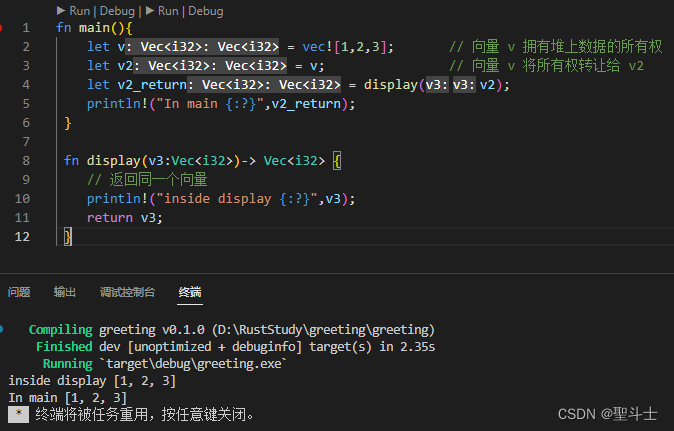
计算图使用图（由节点和边构成的图）来表达算式。

如图，我们用节点代表运算符号，用边代表传入的参数，即可算出购买苹果和橘子的总价格。

2 计算图的局部计算

局部计算意味着每个节点只处理和其相关的运算，通过汇总各个节点计算结果得到最终答案。利用局部计算的性质我们可以通过局部推全局。如上例中如果我们直到总价格为715， 苹果的总价为200，我们可以直接推得橘子的总价，而不需要计算和橘子相关的节点。

计算图的优势之一就在于可以局部计算和保留中间计算结果

3 链式法则

链式法则（chain rule）是计算复合函数导数的一种方法。如z为t的函数，t为x的函数，那dz/dx就等于dz/dt • dt/dx

例：
z = t^2
t = x + y

∂z/∂x = ∂z/∂t • ∂t/∂x
= 2t • 1
= 2(x + y)

用计算图标示该链式法则计算

在正向传播中，x和y相加得到t，再平方得到z。我们节点输出∂z/∂z （就是1）乘以节点的局部偏导∂z/∂t（**2这一节点中z是关于t的函数，因此偏导为∂z/∂t）得到下一步输入∂z/∂t，在乘上t关于x函数节点偏导∂t/∂x即可得到∂z/∂x的值。

加法和乘法的反向传播

加法反向传播：输入值乘1

对于函数z = x + y。∂z/∂x 和 ∂z/∂y 的值都为1，因此在反向传播中只需要将 ∂L/∂z 乘1

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy

乘法反向传播：乘以另一个输入值

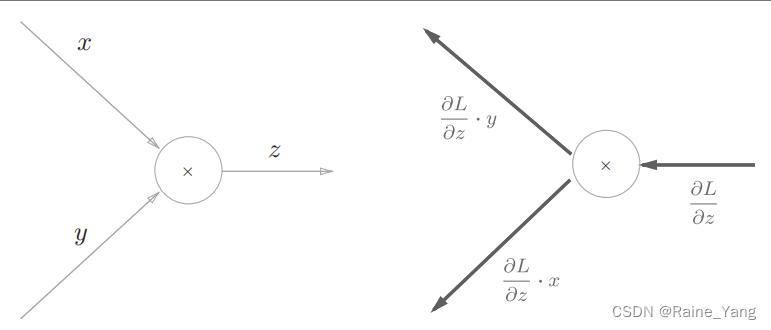
对于函数z = xy。∂z/∂x 的值为y，而∂z/∂y 的值为x。因此在计算∂L关于一个输入值的偏导时，将∂L/∂z 乘以另一个输入值

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y                
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy

利用乘法和加法的反向传播实现购买苹果的计算

# coding: utf-8
from layer_naive import *


apple = 100
apple_num = 2
tax = 1.1

mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dTax:", dtax)

price: 220
dApple: 2.2
dApple_num: 110
dTax: 200

在反向传播时，执行各函数顺序与正向传播相反。正向传播函数的返回值在反向传播时作为函数参数

输出值的意义在于每改变1单位输入值对输出（总价）的影响。如dApple = 2.2意味着每总价一个苹果，对总价增加2.2

例二：购买苹果和橘子例子。和前面购买苹果例子原理完全相同

# coding: utf-8
from layer_naive import *

apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)  # (1)
orange_price = mul_orange_layer.forward(orange, orange_num)  # (2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)  # (3)
price = mul_tax_layer.forward(all_price, tax)  # (4)

# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)  # (4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)  # (3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)  # (2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # (1)

print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dOrange:", dorange)
print("dOrange_num:", int(dorange_num))
print("dTax:", dtax)