一、理解BN必备的前置知识（BN, LN等一系列Normalization方法的动机）
Feature Scaling（特征归一化/Normalization）:通俗易懂理解特征归一化对梯度下降算法的重要性

总结一下得出的结论：
（以下举的例子是针对channel这个维度数据的分布，其余维度同理。值得注意的是：一个minibatch的图像在神经网络中的每一层输出的特征数据都是多维的：N×HW×C，所以任何一个维度都可以进行Normalization）
特征未归一化前，优化目标（loss）的等值图由于参数（对应下文的θ1和θ2）取值范围的不同成狭长的椭圆形（想象成空间中的一个碗，碗口的形状是椭圆形，梯度下降是想到达碗底）。为什么参数的取值范围会不同呢？比如有x1和x2两个特征，分别对应的参数是θ1和θ2，输出的特征就是y = θ1×x1+θ2×x2， 我们可以把x1和x2看成在特征图某个像素位置的两个channel，分别被2个卷积核作用的卷积区域内的特征，且x1特征的取值范围如[0,1000]远大于x2的取值范围如[0,10]，假设x1和x2对因变量y的影响相当，那么θ1的取值范围就应该小于θ2。又因为数值更大的feature得到的梯度更大，下图中θ1对应更大数值的feature即x1，θ2对应更小数值的feature即x2，所以θ1走的step很大，θ2走的step很小，由于梯度方向总是垂直于等高线方向，左图走出的曲线是震荡性较大的“之”字形线路。归一化后，优化目标的等值图会变成右图的圆形，这是因为θ1和θ2的取值范围也变得接近了（基于前面x1和x2对因变量y的影响相当的假设）。θ1和θ2维度的下降速度也变得更为一致，这是因为归一化后由于x1和x2这两个feature的数值接近，所以θ1和θ2参数获得的梯度都差不多，容易更快地通过梯度下降找到最优解。

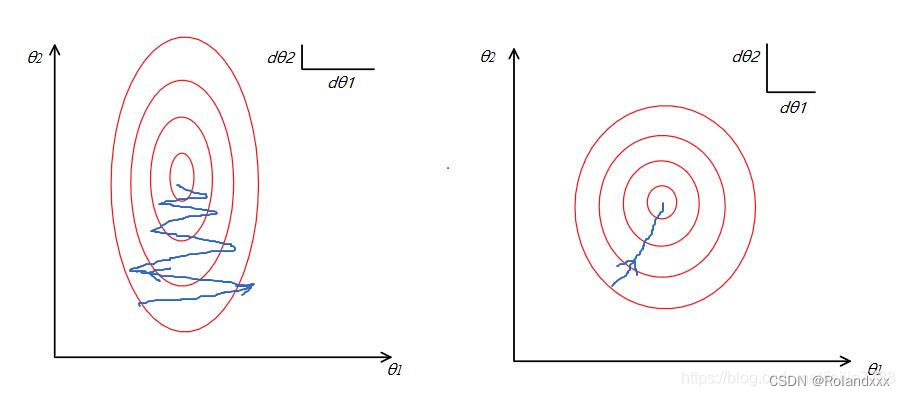
下图即为特征归一化的具体操作：

二、Batch Normalization理解：Batch Normalization的通俗解释

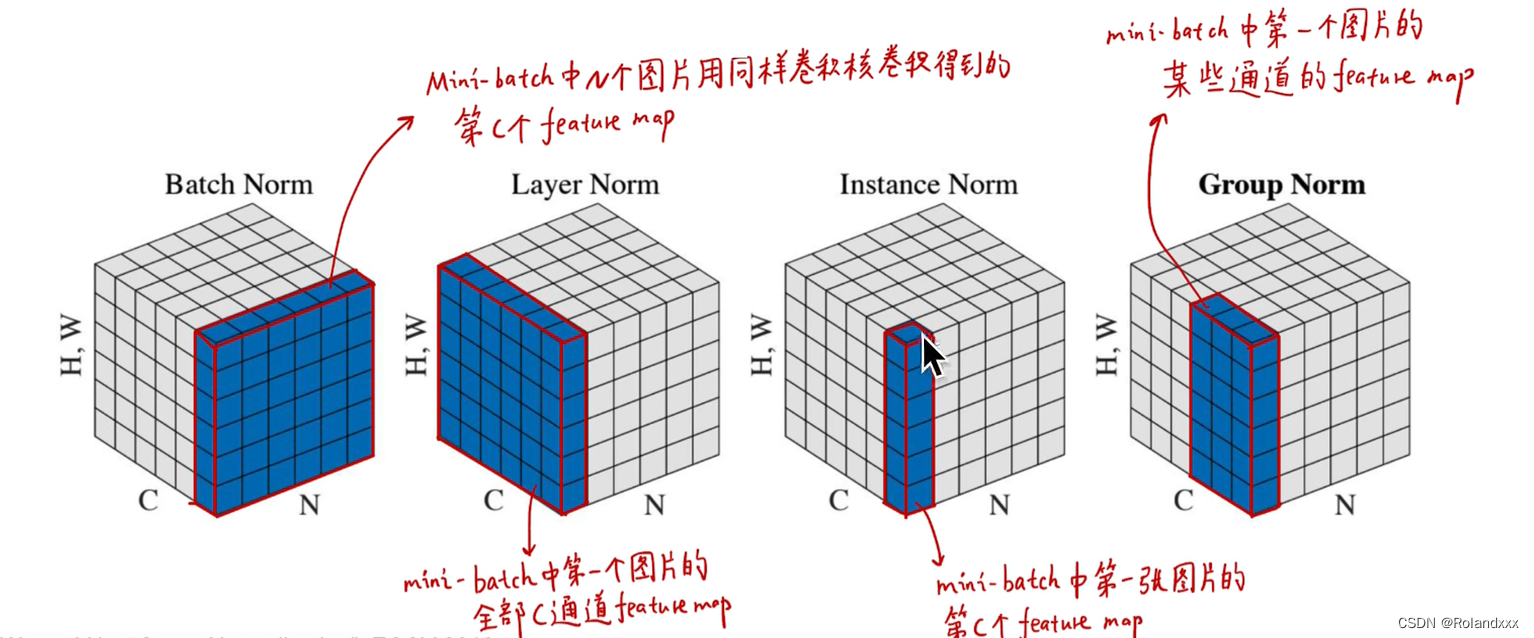
总结：基于第一节讲到的Normalization能为神经网络带来的种种好处，面临的下一个问题就是针对不同的任务，网络每一层的多维的数据在哪个维度进行Normalization是最合适的，于是就有了Batch Normalization(BN) 。在CV中常常使用BN，它是在NHW维度进行了归一化，而Channel维度的信息原封不动，因为可以认为在CV应用场景中，数据在不同channel中的信息很重要，如果对其进行归一化将会损失不同 channel的差异信息。所以总结一下:选择什么样的归一化方式，取决于你关注数据的哪部分信息。如果某个维度信息的差异性很重要，需要被拟合，那就别在那个维度进行归一化。BN针对一个batch内的所有样本的同一通道的元素进行标准化（对哪个维度做Norm，就在其他维度不动的情况下，基于该维度下的所有元素计算均值和方差，然后再做Norm）。

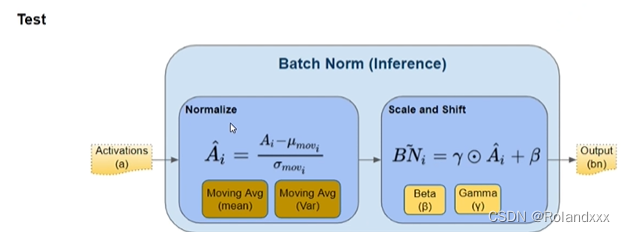
还需注意的是Batch Normalization在训练时和推理时用的参数是不一样的。
训练用的是每个mini-batch训练样本均值和方差，同时还会一直计算Moving Average，Moving Average的初始均值和方差是0和1。
推理用的是所有mini-batches训练样本均值和方差的累计滑动平均结果(Moving Average)，推理中的所有参数都是固定住的。


Refer：
Pytorch Batch Normalization 对照原理实践
【炼丹技巧】指数移动平均（EMA）的原理及PyTorch实现

三、其余Normalization
Layer Normalization（批标准化）：对一个样本内所有通道的元素进行标准化

Instance Normalization（实例标准化）：对一个样本内对每个通道的元素分别进行标准化，即在H*W维度上进行标准化

Group Normalization（组标准化）：对一个样本内对几个通道的元素分别进行标准化