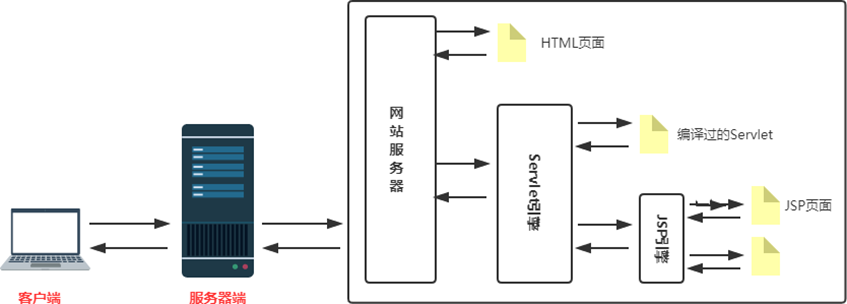
一、搜索
搜索是“暴力法”算法思想的具体实现。
搜索是“通用”的方法。一个问题,如果比较难,那么先尝试一下搜索,或许能启发出更好的算法。
技巧:竞赛时遇到不会的难题,用搜索提交一下,说不定部分判题数据很弱,得分了!
搜索的基本思路:
[BFS] Breadth-First Search,宽度优先搜索,或称为广度优先搜索。
[DFS] Depth-First Search,深度优先搜索。
二、暴力法
利用计算机强大的计算能力和存储能力,实现“暴力法”,把所有可能性都列举出来,一一验证,简单直接!
暴力(蛮力)是有效的技术:
理论上,蛮力法可以解决可计算领域的各种问题。
蛮力法经常用来解决一些较小规模的问题。
对于一些重要的问题蛮力法可以产生一些合理的算法具备一些实用价值,而且不受问题规模的限制。
蛮力法可以作为某类问题时间性能的底限,来衡量同样问题的更高效算法。
暴力的基本方法:
蛮力的基本方法——扫描。
关键——依次处理所有元素。
基本的扫描技术——遍历:
集合的遍历。
线性表的遍历
树的遍历
图的遍历
非线性方程:指f(x)中含有三角函数、指数函数或其他超越函数。
非线性方程,很难或者无法求得精确解。
二分法是一种求解的方法。
三、老鼠走迷宫
BFS:一群老鼠走迷宫
• 老鼠无限多。
• 在每个路口,都派出部分老鼠探索所有没走过的路。
• 走某条路的老鼠,如果碰壁无法前行,就停下。
• 如果到达的路口已经有别的老鼠探索过了,也停下。
• 所有的道路都会走到,而且不会重复。
------>广度优先、全面扩散、逐层递进。DFS:一只老鼠走迷宫
• 只有一只老鼠。
• 在每个路口,都选择先走右边 (当然,选择先走左边也可以),能走多远就走多远。
• 碰壁无法再继续往前走,回退一步,这一次走左边然后继续往下走。
• 能走遍所有的路,而且不会重复 (回退不算重复)。
------>深度优先、一路到底、逐层回退。四、DFS访问示例
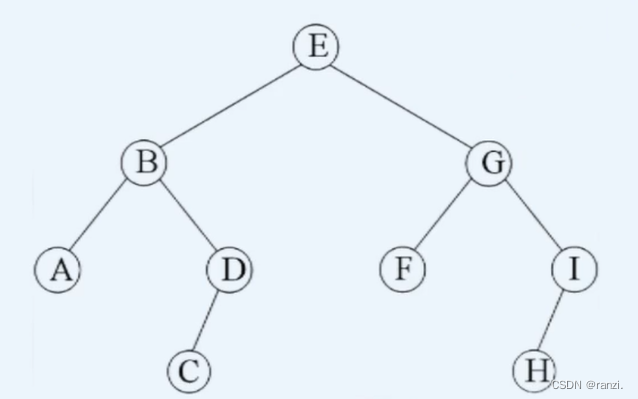
设先访问左节点,后访问右节点,模拟老鼠走迷宫;
访问顺序:EBADCGFIHI。
五、DFS的常见操作
DFS的代码比BFS更简短。
DFS的主要操作:
时间戳
DFS序
树深度
子树节点数
中序输出
先序输出
后序输出
六、DFS基础:递归和记忆化搜索
形式上,递归函数是“自己调用自己”,是一个不断“重复”的过程。
递归的思想,是把大问题逐步缩小,直到变成最小的同类问题的过程,而最后的小问题的解是已知的,一般是给定的初始条件。到达最小问题后,再“回溯”,把小问题的解逐个带回给更大的问题,最终最大问题也得到了解决。
递归有两个过程:递归前进、递归返回(回溯)。
在递归的过程中,由于大问题和小问题的解决方法完全一样,那么大问题的代码和小问题的代码可以写成一样。
一个递归函数,直接调用自己,实现了程序的复用。
七、例子:斐波那契数列
递推式: f(n) = f(n-1) + f(n-2)
即:前两个数相加得到下一个数。
要求:打印第20个数。普通方法实现

递归方法实现

函数fib(20)计算斐波那契数。
递归过程:
递归前进: fib(20) = fib(19) + fib(18)
递归前进: fib(19) = fib(18) + fib(17)
递归前进: fib(18) = fib(17) + fib(16)
......
递归前进: fib(3) = fib(2) + fib(1)
到达终止条件: fib(2) = 1,fib(1) = 1
回溯过程 :
递归返回: fib(3) = fib(2) + fib(1) =1+1=2
递归返回: fib(4) = fib(3) + fib(2) =2+1=3
......
递归返回: fib(20)=fib(19)+fib(18)=4181+2584=6765
递归的次数:
递推和递归两种代码,结果一样,计算量差别巨大。
递推代码:一个for循环,计算20次。
递归代码: 计算第20个斐波那契数,共计算cnt = 13529次。

为什么斐波那契的递归代码如此低效?
return fib(n-1) + fib(n-2)递归调用了自己2次,倍增。
计算fib(n)时,共执行了O(2的n次方)次递归。
不过,很多递归函数只调用自己一次不个额外增加计算量。
改进:记忆法
递归的过程中做了重复工作,例如fb(3)计算了2次,其实只算1次就够了,为避免递归时重复计算,可以在子问题得到解决时,就保存结果,再次需要这个结果时,直接返回保存的结果就行了,不继续递归下去。
这种存储已经解决的子问题结果的技术称为“记忆化(Memoization)”。
记忆化是递归的常用优化技术。动态规划也常常用递归写代码,记忆化也是动态规划的关键技术。

递归的关键问题:递归深度不能太大。
Python默认递归深度1000,如果递归深度太大,提示“maximum recursion depth exceeded in comparison”。
用sys.setrecursionlimit()设置递归深度。
常常有深度大于1000的递归题目。
八、DFS的代码框架
DFS的框架,请在大量编码的基础上,再回头体会这个框架的作用。

在DFS框架中,最让初学者费解的是第10行和第12行。
第10行的used[i] = 1,称为“保存现场”,或“占有现场”。
第12行的used[i] = 0,称为“恢复现场”,或“释放现场”。
九、例子:DFS搜索和输出所有路径




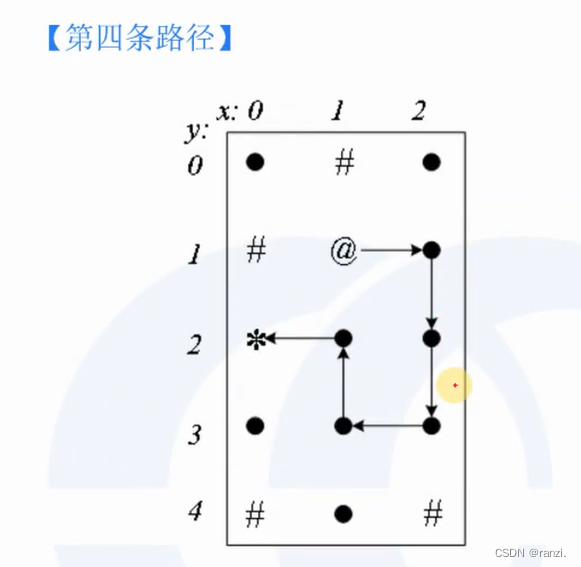




十、总结:路径问题BFS和DFS
搜所有的路径,应该用DFS;如果只搜最短路径,应该用BFS。
在一张图上,从起点到终点的所有路径数量是一个天文数字,读者可以用上面的代码试试一个8x8的图,看看路径总数是多少。但是搜最短的路径就比较简单,并不需要把所有路径搜出来之后再比较得到最短路,用BFS可以极快地搜到最短路。DFS适合用来处理暴力搜所有情况的题目。