想查看其他题的真题及题解的同学可以前往查看:CCF-CSP真题附题解大全
| 试题编号: | 202212-2 |
| 试题名称: | 训练计划 |
| 时间限制: | 1.0s |
| 内存限制: | 512.0MB |
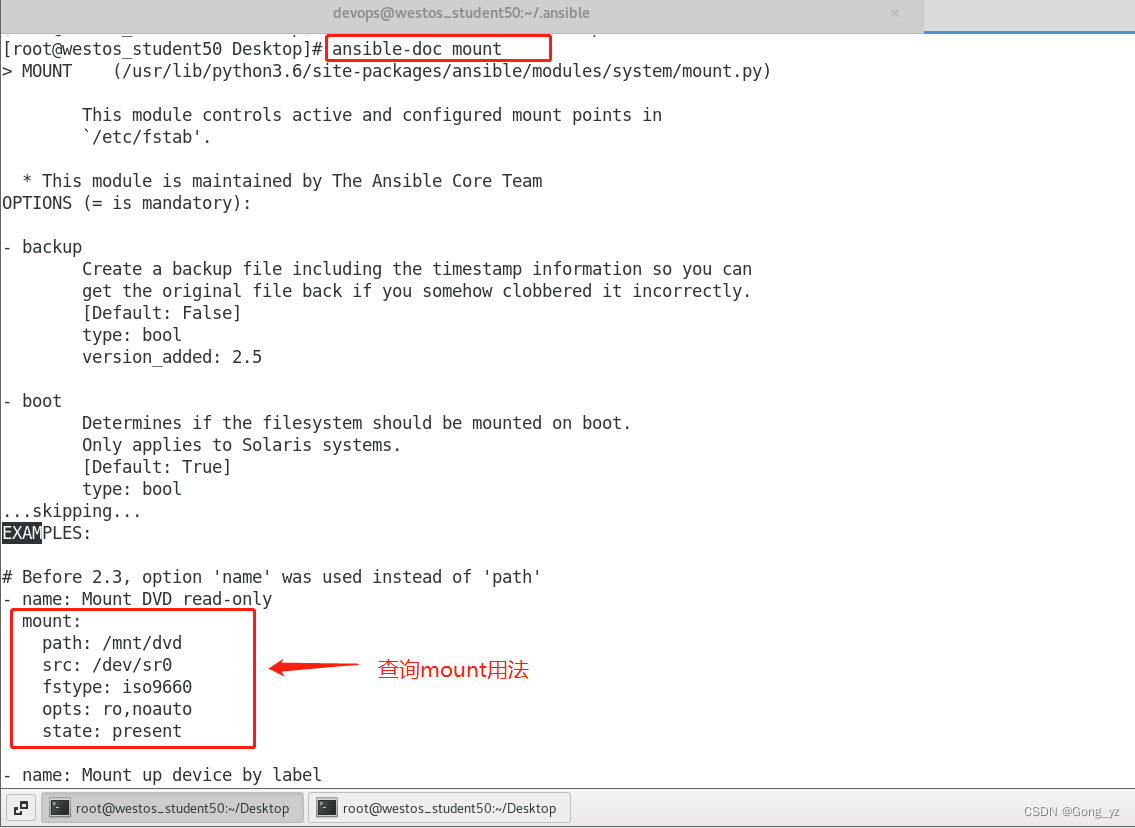
| 问题描述: | 问题背景西西艾弗岛荒野求生大赛还有 n 天开幕! 问题描述为了在大赛中取得好成绩,顿顿准备在 n 天时间内完成“短跑”、“高中物理”以及“核裂变技术”等总共 m 项科目的加强训练。其中第 i 项(1≤i≤m)科目编号为 i,也可简称为科目 i。已知科目 i 耗时 ti 天,即如果从第 a 天开始训练科目 i,那么第 a+ti−1 天就是该项训练的最后一天。 大部分科目的训练可以同时进行,即顿顿在同一天内可以同时进行多项科目的训练,但部分科目之间也存在着依赖关系。如果科目 i 依赖科目 j,那么只能在后者训练结束后,科目 i 才能开始训练。具体来说,如果科目 j 从第 a 天训练到第 a+tj−1 天,那么科目 i 最早只能从第 a+tj 天开始训练。还好,顿顿需要训练的 m 项科目依赖关系并不复杂,每项科目最多只依赖一项别的科目,且满足依赖科目的编号小于自己。那些没有任何依赖的科目,则可以从第 1 天就开始训练。 对于每一项科目,试计算: 1)最早开始时间:该科目最早可以于哪一天开始训练? 2)最晚开始时间:在不耽误参赛的前提下(n 天内完成所有训练),该科目最晚可以从哪一天开始训练? n 天内完成所有训练,即每一项科目训练的最后一天都要满足 ≤n。需要注意,顿顿如果不能在 n 天内完成全部 m 项科目的训练,就无法参加大赛。这种情况下也就不需要再计算“最晚开始时间”了。 输入格式从标准输入读入数据。 输入共三行。 输入的第一行包含空格分隔的两个正整数 n 和 m,分别表示距离大赛开幕的天数和训练科目的数量。 输入的第二行包含空格分隔的 m 个整数,其中第 i 个(1≤i≤m)整数 pi 表示科目 i 依赖的科目编号,满足 0≤pi<i;pi=0 表示科目 i 无依赖。 输入的第三行包含空格分隔的 m 个正整数,其中第 i 个(1≤i≤m)数 ti 表示训练科目 i 所需天数,满足 1≤ti≤n。 输出格式输出到标准输出中。 输出共一行或两行。 输出的第一行包含空格分隔的 m 个正整数,依次表示每项科目的最早开始时间。 如果顿顿可以在 n 天内完成全部 m 项科目的训练,则继续输出第二行,否则输出到此为止。 输出的第二行包含空格分隔的 m 个正整数,依次表示每项科目的最晚开始时间。 样例 1 输入
样例 1 输出
样例 1 说明五项科目间没有依赖关系,都可以从第 1 天就开始训练。 10 天时间恰好可以完成所有科目的训练。其中科目 1 耗时仅 1 天,所以最晚可以拖延到第 10 天再开始训练;而科目 5 耗时 10 天,必须从第 1 天就开始训练。 样例 2 输入
样例 2 输出
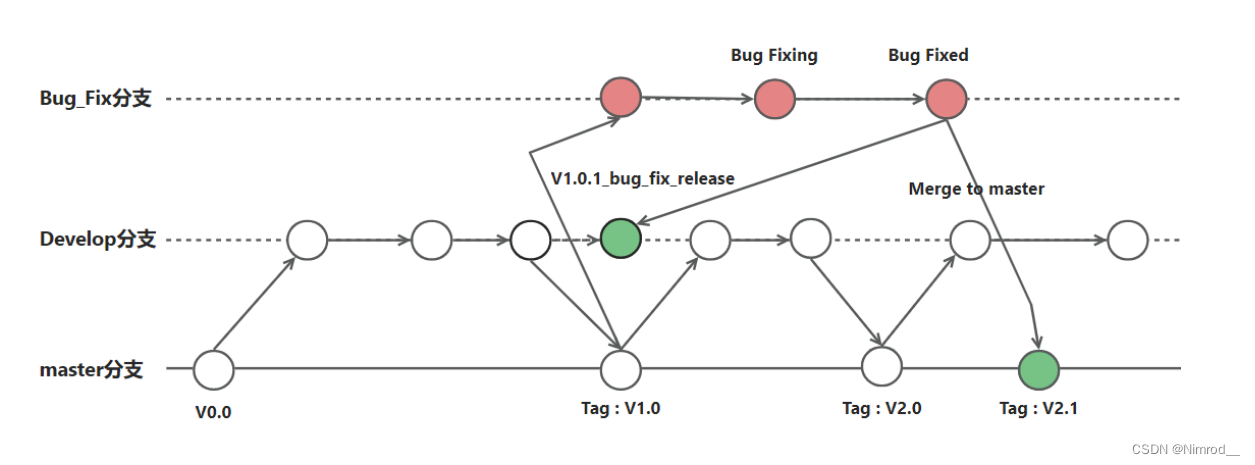
样例 2 说明七项科目间的依赖关系如图所示,其中仅科目 5 无法在 10 天内完成训练。
具体来说,科目 5 依赖科目 2、科目 2 又依赖于科目 1,因此科目 5 最早可以从第 4 天开始训练。 样例 3 输入
样例 3 输出
子任务70 的测试数据满足:顿顿无法在 n 天内完成全部 m 项科目的训练,此时仅需输出一行“最早开始时间”; 全部的测试数据满足 0<n≤365 且 0<m≤100。 |
真题来源:训练计划
感兴趣的同学可以如此编码进去进行练习提交
直接无脑解(70分):
n, m = map(int,input().split())
p = [0]+[i for i in map(int,input().split())]
t = [0]+[i for i in map(int,input().split())]
earliest = [0 for _ in range(m+1)]
latest = [0 for _ in range(m+1)]
for i in range(1,m+1):
if p[i]==0:
earliest[i] = 1
latest[i] = n-t[i]+1
else:
earliest[i] = earliest[p[i]]+t[p[i]]
latest[i] = n-latest[p[i]]-t[i]
print(*earliest[1:])
if min(latest)>0:
print(*latest[1:])运行结果:

错误解析:
这种解法属于第二题看到题直白写就好,这个题解虽然有70分,但是我在写的时候没有考虑好最晚开始时间是否输出的问题,这是不符题意的,但也有70分入手。
满分题解:



![[Android Studio] Android Studio Virtual Device虚拟机的功能试用](https://img-blog.csdnimg.cn/24b696d76d374a9992017e1625389592.gif)