一、卷积相关

用一个f×f的过滤器卷积一个n×n的图像，假如padding为p，步幅为s，输出大小则为：

$[\frac{n+2p-f}{s}+1]\times [\frac{n+2p-f}{s}+1]$

[]表示向下取整（floor)

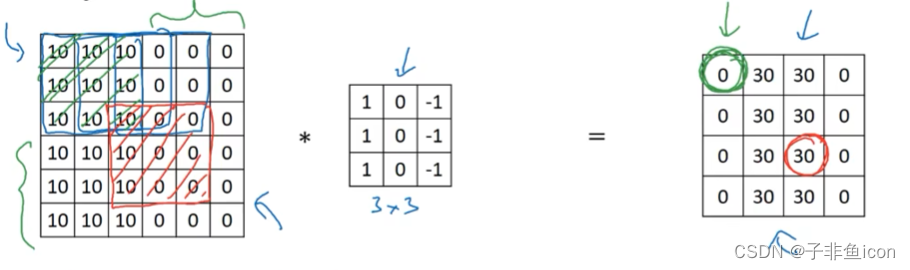
大部分深度学习的方法对过滤器不做翻转等操作，直接相乘，更像是互相关，但约定俗成叫卷积运算。

二、三维卷积

图片的数字通道数必须和过滤器中的通道数相匹配。

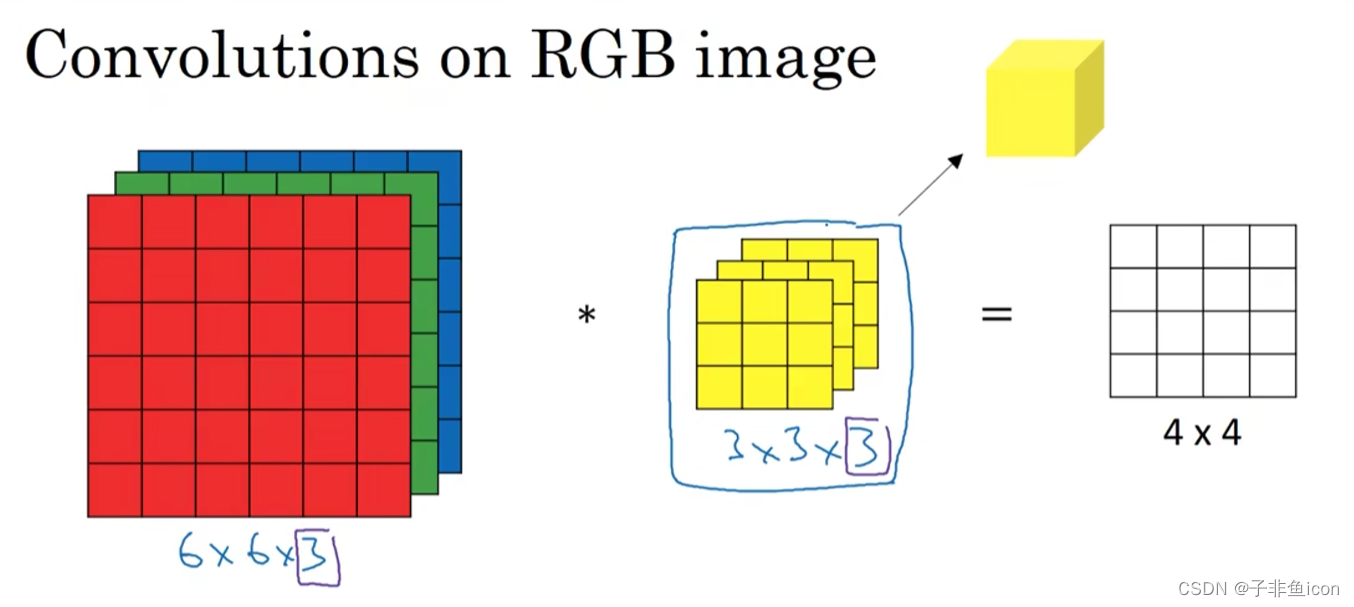
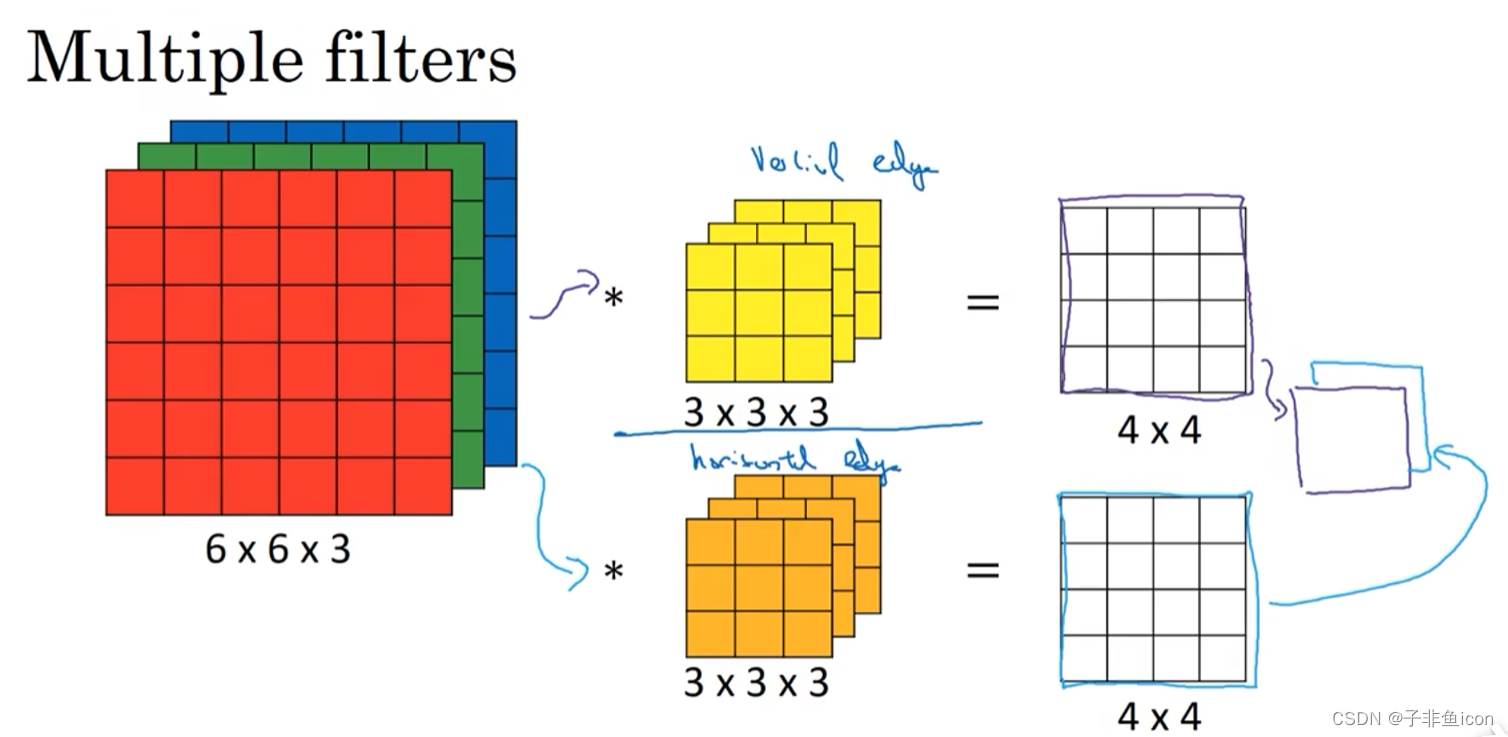
三维卷积相当于一个立方体与所有通道都乘起来然后求和。可以设计滤波器使得其得到单一通道，如红色的边缘特征。

卷积核通道数等于输入通道数，卷积核个数等于输出通道数。

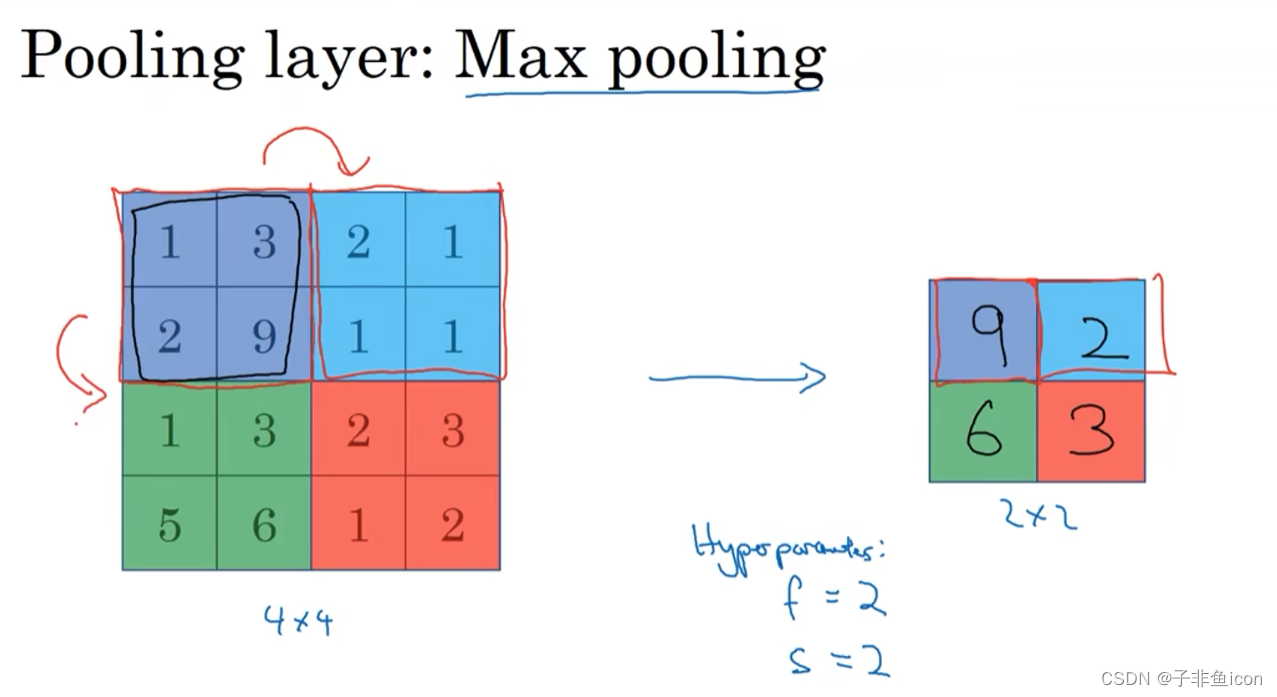
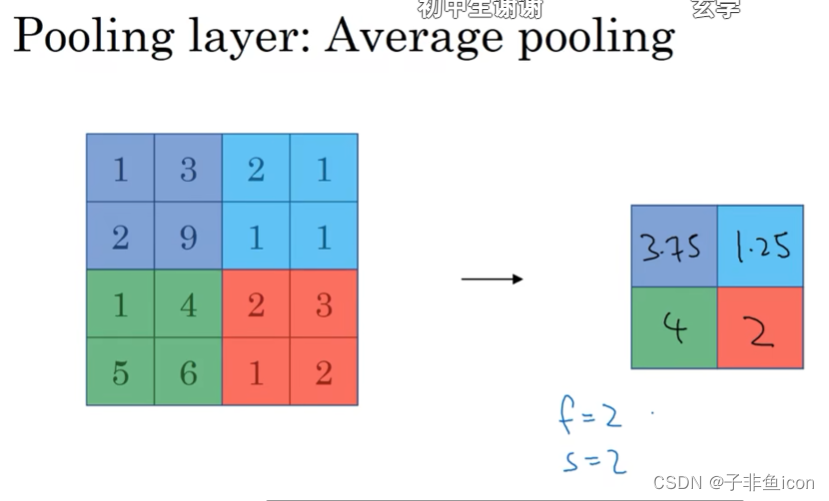
三、池化层

最大池化


平均池化

四、为什么使用卷积

1.参数共享。

2.稀疏连接。

五、两个重要课后题

六、第一周课后作业

使用Pytorch来实现卷积神经网络，然后应用到手势识别中

代码：

import h5py
import time
import torch
import numpy as np
import torch.nn as nn
import matplotlib.pyplot as plt

#import cnn_utils

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 加载数据集
def load_dataset():
    train_dataset = h5py.File('datasets/train_signs.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:])  # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:])  # your train set labels

    test_dataset = h5py.File('datasets/test_signs.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:])  # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:])  # your test set labels

    classes = np.array(test_dataset["list_classes"][:])  # the list of classes

    train_set_y_orig = train_set_y_orig.reshape((train_set_y_orig.shape[0], 1))
    test_set_y_orig = test_set_y_orig.reshape((test_set_y_orig.shape[0], 1))

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

print(X_train_orig.shape) # (1080, 64, 64, 3),训练集1080张，图像大小是64*64
print(Y_train_orig.shape) #  (1080, 1)
print(X_test_orig.shape) # (120, 64, 64, 3)，测试集120张
print(Y_test_orig.shape)  # (120, 1)
print(classes.shape) # (6,) 一共6种类别，0，1，2，3，4，5

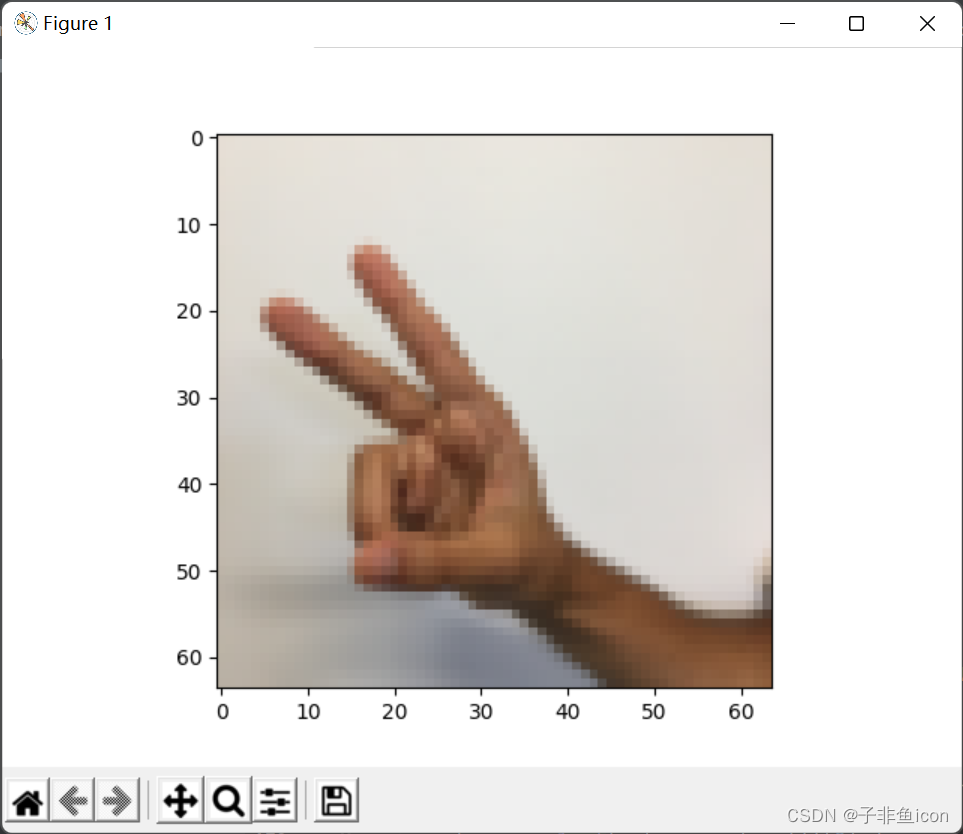
index = 6
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[index,:])))
plt.show()

# 把尺寸(H x W x C)转为(C x H x W) ，即通道在最前面；归一化数据集
X_train = np.transpose(X_train_orig, (0, 3, 1, 2))/255          # 将维度转为(1080, 3, 64, 64)
X_test = np.transpose(X_test_orig, (0, 3, 1, 2))/255            # 将维度转为(120, 3, 64, 64)
Y_train = Y_train_orig
Y_test = Y_test_orig

# 转成Tensor方便后面的训练
X_train = torch.tensor(X_train, dtype=torch.float)
X_test = torch.tensor(X_test, dtype=torch.float)
Y_train = torch.tensor(Y_train, dtype=torch.float)
Y_test = torch.tensor(Y_test, dtype=torch.float)

print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)

# 使用交叉熵损失函数不用转化为独热编码
# LeNet模型
class ConvNet(nn.Module):
    def __init__(self):
        super(ConvNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(in_channels=3, out_channels=8, kernel_size=4, padding=1, stride=1), # in_channels, out_channels, kernel_size 二维卷积
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=8, stride=8, padding=4), # kernel_size=2, stride=2；原函数就是'kernel_size', 'stride', 'padding'的顺序

            nn.Conv2d(8, 16, 2, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=4, stride=4, padding=2)
        )
        self.fc = nn.Sequential(
            nn.Linear(16*3*3, 6),  # 16*3*3 向量长度为通道、高和宽的乘积
            nn.Softmax(dim=1)
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.reshape(img.shape[0], -1))  # 全连接层块会将小批量中每个样本变平
        return output

net = ConvNet()
print(net)

# 定义损失函数
loss = nn.CrossEntropyLoss()


# 训练模型
def model(net, X_train, Y_train, device, lr=0.001, batch_size=32, num_epochs=1500,  print_loss=True, is_plot=True):

    net = net.to(device)
    print("training on ", device)
    # 定义优化器
    optimizer = torch.optim.Adam(net.parameters(), lr=lr, betas=(0.9, 0.999))

    # 将训练数据的特征和标签组合
    dataset = torch.utils.data.TensorDataset(X_train, Y_train)
    train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)

    train_l_list, train_acc_list = [], []
    for epoch in range(num_epochs):

        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            X = X.to(device)
            y = y.to(device)
            y_hat = net(X)
            y = y.squeeze(
                1).long()  # .squeeze()用来将[batch_size,1]降维至[batch_size],.long用来将floatTensor转化为LongTensor，loss函数对类型有要求
            l = loss(y_hat, y).sum()
            # print(y.shape,y_hat.shape)
            # print(l)

            # 梯度清零
            optimizer.zero_grad()

            l.backward()
            optimizer.step()

            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            # print(y_hat.argmax(dim=1).shape,y.shape)
            n += y.shape[0]
        train_l_list.append(train_l_sum / n)
        train_acc_list.append(train_acc_sum / n)
        if print_loss and ((epoch + 1) % 10 == 0):
            print('epoch %d, loss %.4f, train acc %.3f' % (epoch + 1, train_l_sum / n, train_acc_sum / n))

    # 画图展示
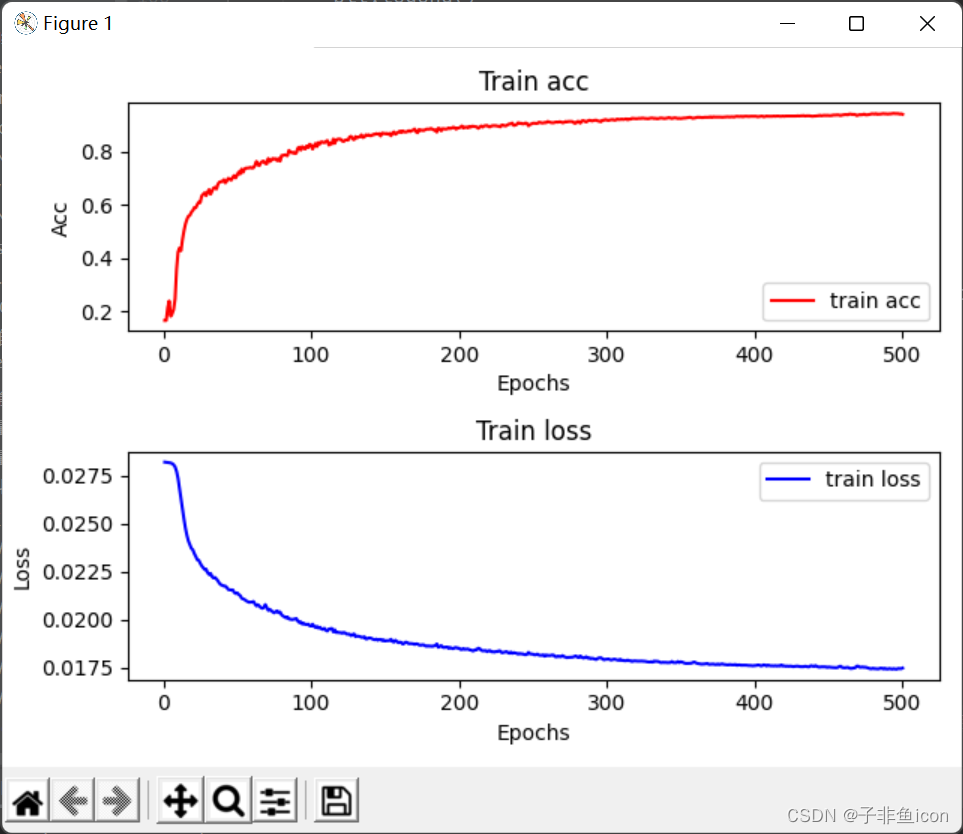
    if is_plot:
        epochs_list = range(1, num_epochs + 1)

        plt.subplot(211)
        plt.plot(epochs_list, train_acc_list, label='train acc', color='r')

        plt.title('Train acc')
        plt.xlabel('Epochs')
        plt.ylabel('Acc')
        plt.tight_layout()
        plt.legend()

        plt.subplot(212)
        plt.plot(epochs_list, train_l_list, label='train loss', color='b')
        plt.title('Train loss')
        plt.xlabel('Epochs')
        plt.ylabel('Loss')
        plt.tight_layout()
        plt.legend()
        plt.show()

    return train_l_list, train_acc_list


#开始时间
start_time = time.clock()
#开始训练
train_l_list, train_acc_list = model(net, X_train, Y_train, device, lr=0.0009, batch_size=64, num_epochs=500, print_loss=True, is_plot=True)
#结束时间
end_time = time.clock()
#计算时差
print("CPU的执行时间 = " + str(end_time - start_time) + " 秒" )


#计算分类准确率
def evaluate_accuracy(X_test, Y_test, net, device=None):


    if device is None and isinstance(net, torch.nn.Module):
        # 如果没指定device就使用net的device
        device = list(net.parameters())[0].device  # 未指定的话，就是cpu

    X_test = X_test.to(device)
    Y_test = Y_test.to(device)

    acc = (net(X_test).argmax(dim=1) == Y_test.squeeze()).sum().item()
    acc = acc / X_test.shape[0]

    return acc

accuracy_train = evaluate_accuracy(X_train, Y_train, net)
print("训练集的准确率:", accuracy_train)

accuracy_test = evaluate_accuracy(X_test, Y_test, net)
print("测试集的准确率:", accuracy_test)

输出：

(1080, 64, 64, 3)
(1080, 1)
(120, 64, 64, 3)
(120, 1)
(6,)
y = 2
torch.Size([1080, 3, 64, 64])
torch.Size([120, 3, 64, 64])
torch.Size([1080, 1])
torch.Size([120, 1])
ConvNet(
  (conv): Sequential(
    (0): Conv2d(3, 8, kernel_size=(4, 4), stride=(1, 1), padding=(1, 1))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=8, stride=8, padding=4, dilation=1, ceil_mode=False)
    (3): Conv2d(8, 16, kernel_size=(2, 2), stride=(1, 1), padding=(1, 1))
    (4): ReLU()
    (5): MaxPool2d(kernel_size=4, stride=4, padding=2, dilation=1, ceil_mode=False)
  )
  (fc): Sequential(
    (0): Linear(in_features=144, out_features=6, bias=True)
    (1): Softmax(dim=1)
  )
)
training on  cuda
epoch 10, loss 0.0274, train acc 0.423
epoch 20, loss 0.0236, train acc 0.580
epoch 30, loss 0.0224, train acc 0.649
epoch 40, loss 0.0218, train acc 0.689
epoch 50, loss 0.0214, train acc 0.713
epoch 60, loss 0.0209, train acc 0.739
epoch 70, loss 0.0206, train acc 0.755
epoch 80, loss 0.0202, train acc 0.786
epoch 90, loss 0.0201, train acc 0.795
epoch 100, loss 0.0197, train acc 0.825
epoch 110, loss 0.0194, train acc 0.839
epoch 120, loss 0.0193, train acc 0.847
epoch 130, loss 0.0191, train acc 0.857
epoch 140, loss 0.0190, train acc 0.860
epoch 150, loss 0.0189, train acc 0.868
epoch 160, loss 0.0188, train acc 0.878
epoch 170, loss 0.0187, train acc 0.886
epoch 180, loss 0.0186, train acc 0.885
epoch 190, loss 0.0185, train acc 0.886
epoch 200, loss 0.0185, train acc 0.890
epoch 210, loss 0.0184, train acc 0.895
epoch 220, loss 0.0184, train acc 0.894
epoch 230, loss 0.0183, train acc 0.900
epoch 240, loss 0.0182, train acc 0.909
epoch 250, loss 0.0182, train acc 0.907
epoch 260, loss 0.0181, train acc 0.914
epoch 270, loss 0.0181, train acc 0.909
epoch 280, loss 0.0180, train acc 0.914
epoch 290, loss 0.0180, train acc 0.916
epoch 300, loss 0.0179, train acc 0.919
epoch 310, loss 0.0179, train acc 0.923
epoch 320, loss 0.0178, train acc 0.924
epoch 330, loss 0.0178, train acc 0.927
epoch 340, loss 0.0178, train acc 0.926
epoch 350, loss 0.0178, train acc 0.925
epoch 360, loss 0.0177, train acc 0.928
epoch 370, loss 0.0177, train acc 0.931
epoch 380, loss 0.0176, train acc 0.931
epoch 390, loss 0.0176, train acc 0.932
epoch 400, loss 0.0176, train acc 0.933
epoch 410, loss 0.0176, train acc 0.933
epoch 420, loss 0.0176, train acc 0.933
epoch 430, loss 0.0176, train acc 0.934
epoch 440, loss 0.0175, train acc 0.934
epoch 450, loss 0.0175, train acc 0.936
epoch 460, loss 0.0175, train acc 0.939
epoch 470, loss 0.0176, train acc 0.938
epoch 480, loss 0.0175, train acc 0.943
epoch 490, loss 0.0174, train acc 0.942
epoch 500, loss 0.0175, train acc 0.941
CPU的执行时间 = 67.5224961 秒
训练集的准确率: 0.9425925925925925
测试集的准确率: 0.8333333333333334

七、经典网络

LeNet：

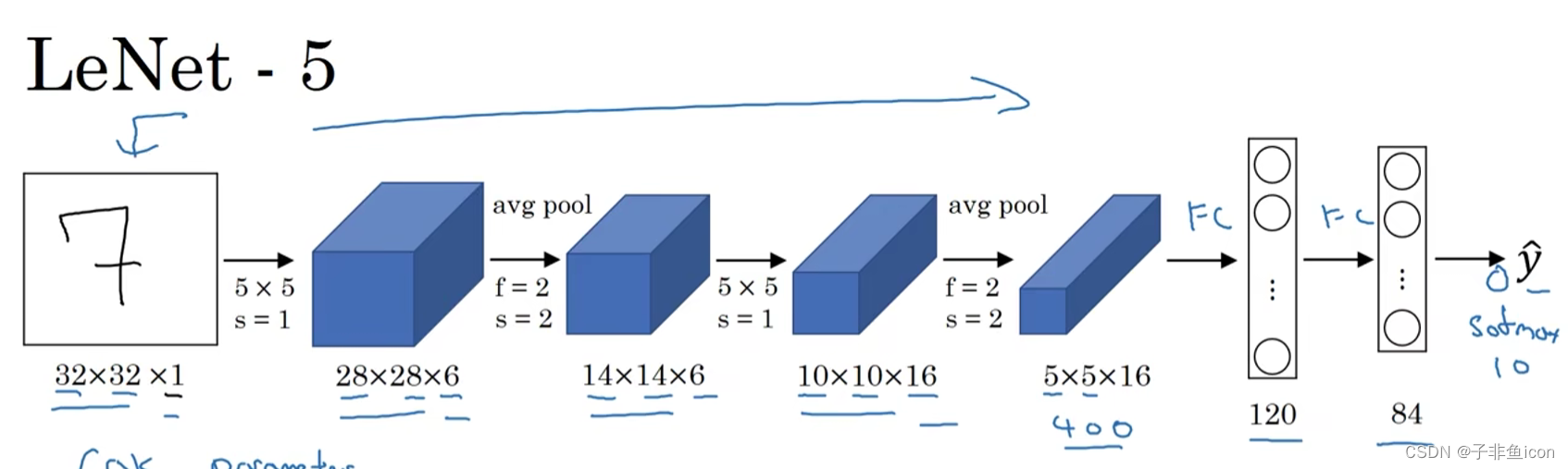
AlexNet

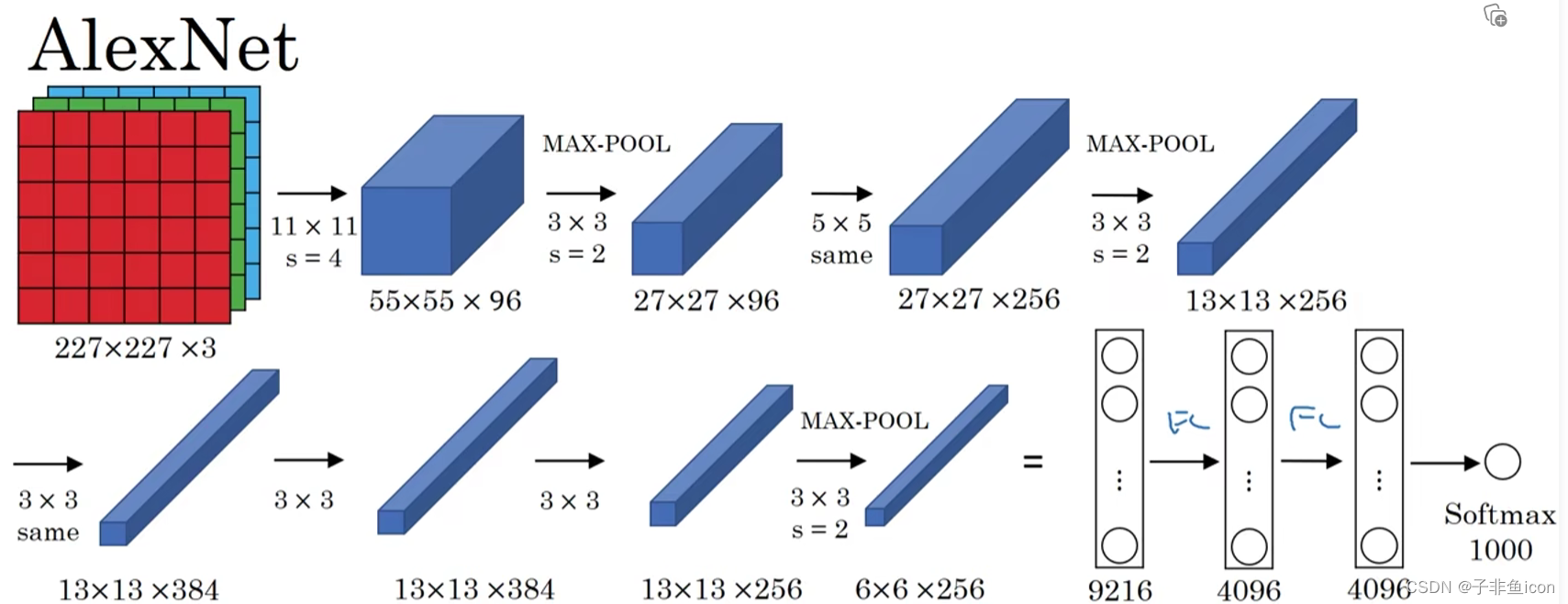
VGG-16

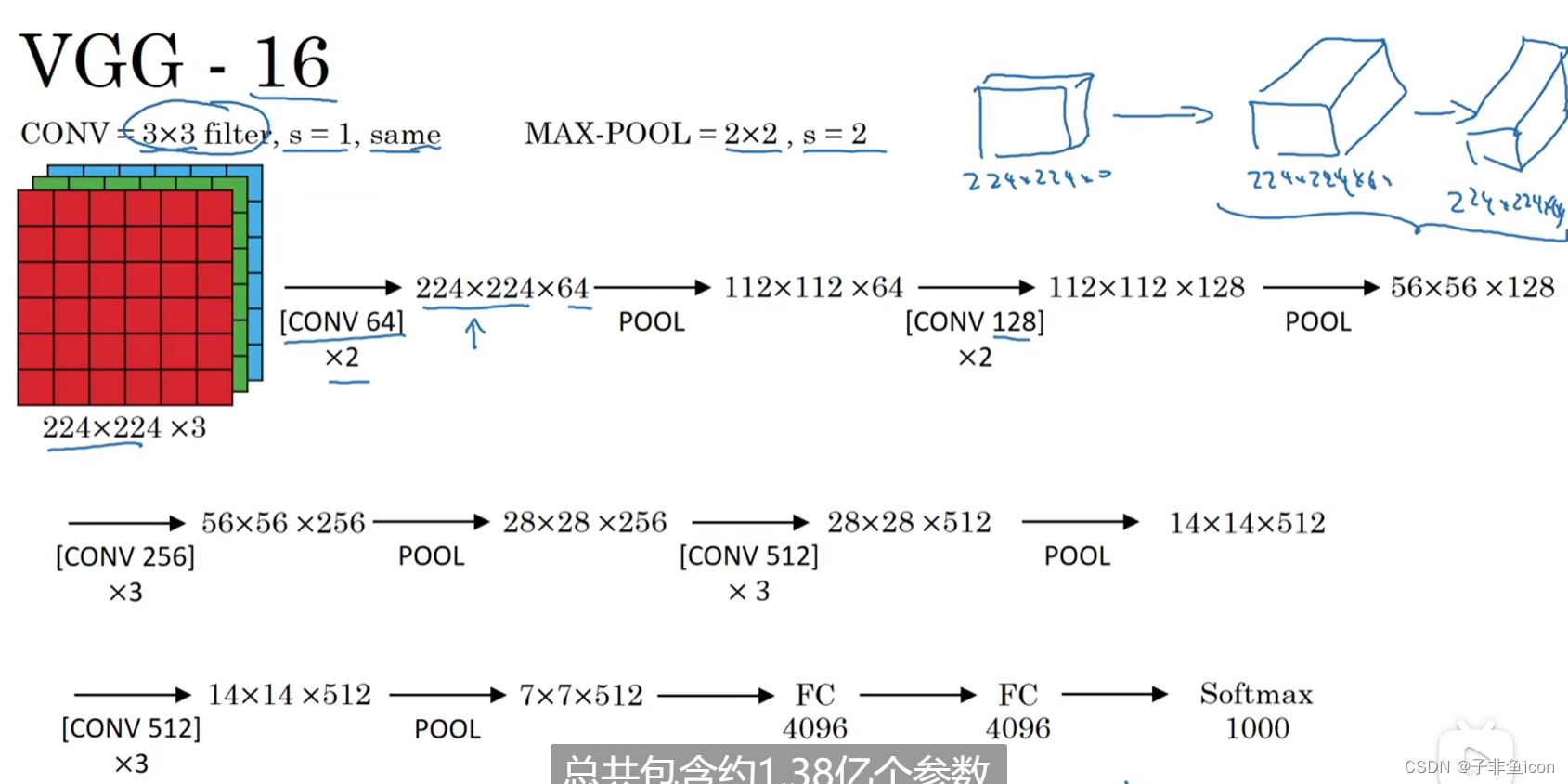
八、残差网络

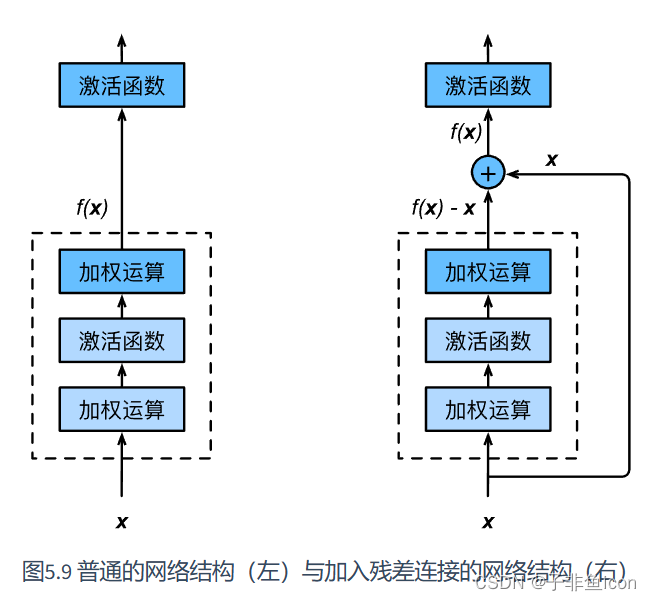
残差网络起作用的主要原因是：这些残差块学习恒等函数非常容易，能确定网络性能不会受到影响，很多时候甚至可以提高效率，或者说至少不会降低网络的效率，因此，创建类似残差网络可以提升网络性能。

九、1×1卷积（Network in Network)

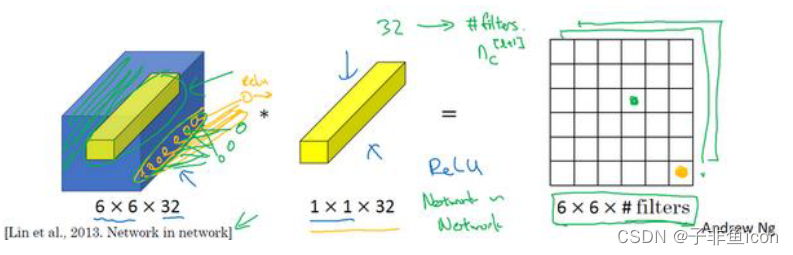
这个1x1×32过滤器中的32个数字可以这样理解，一个神经元的输入是32个数字（输入图片中左下角位置32个通道中的数字），即相同高度和宽度上某一切片上的32个数字，这32个数字具有不同通道，乘以32个权重（将过滤器中的32个数理解为权重)，然后应用ReLU非线性函数，输出相应的结果。

1×1卷积压缩信道数量并减少计算

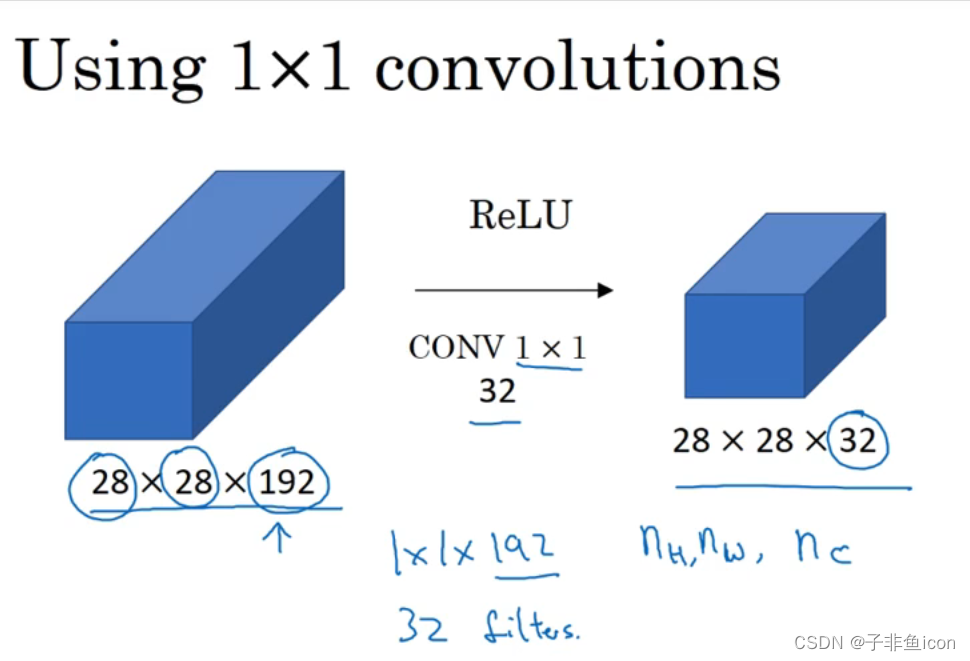
1x1卷积层就是这样实现了一些重要功能的(doing something pretty non-trivial)，它给神经网络添加了一个非线性函数，从而减少或保持输入层中的通道数量不变，当然如果你愿意，也可以增加通道数量。

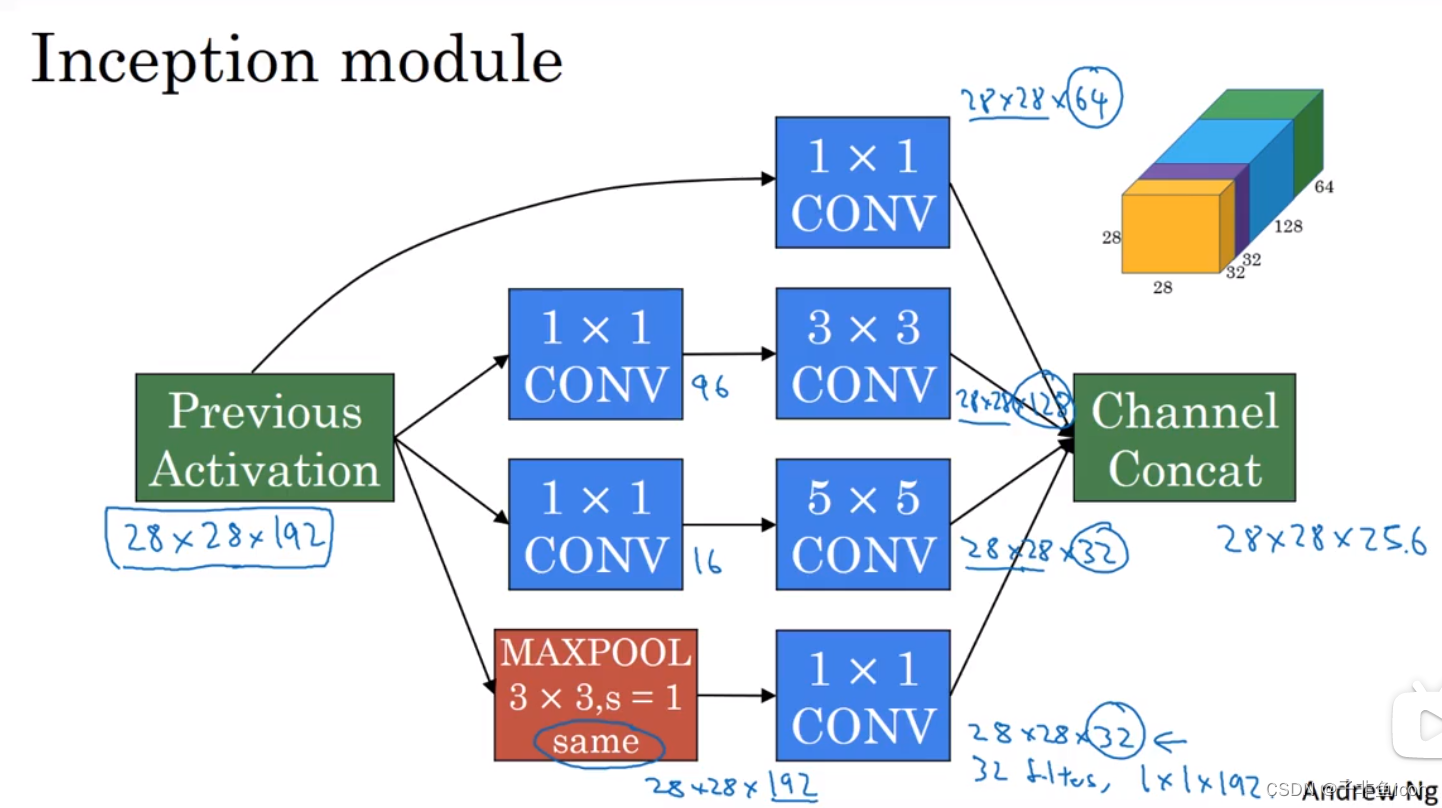
十、谷歌Inception网络

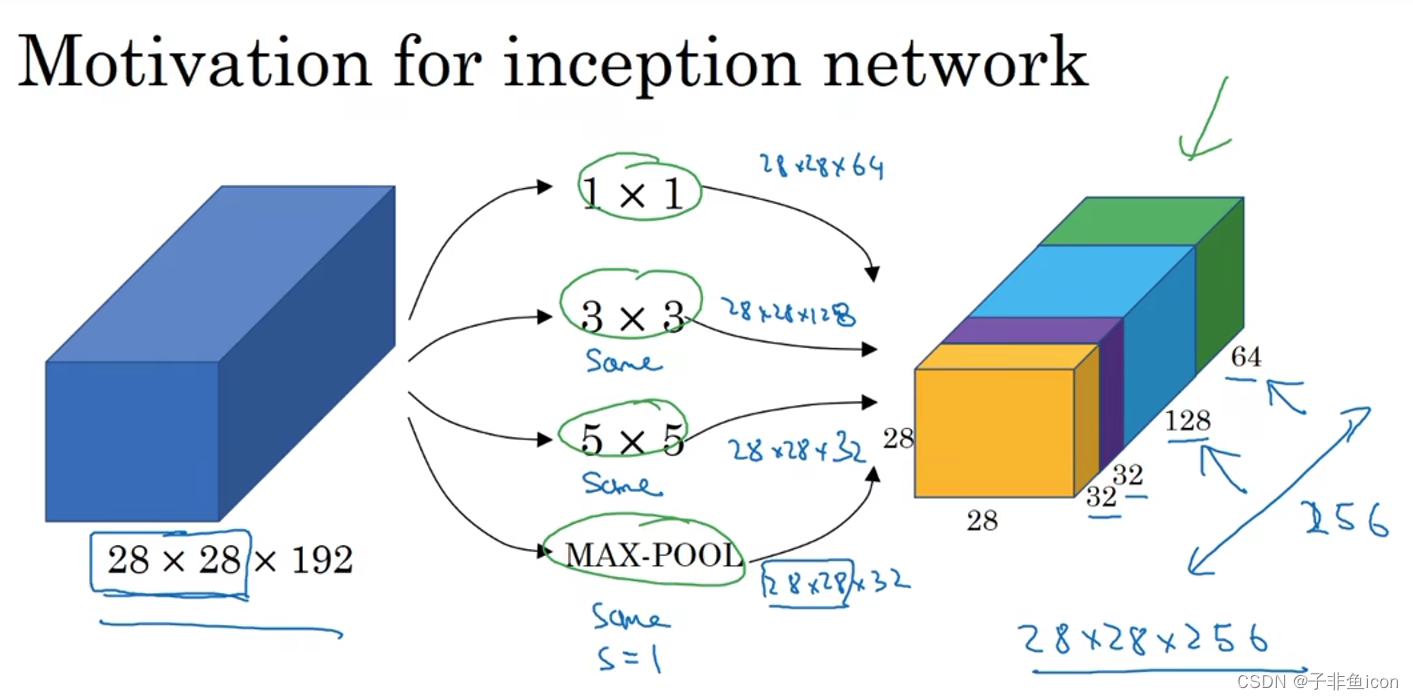
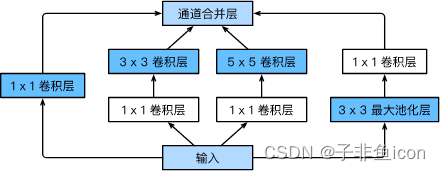
Inception块里有4条并行的线路。前3条线路使用窗口大小分别是1×1、3×3和5×5的卷积层来抽取不同空间尺寸下的信息，其中中间2个线路会对输入先做1×1卷积来减少输入通道数，以降低模型复杂度。第四条线路则使用3×3最大池化层，后接1×1卷积层来改变通道数。4条线路都使用了合适的填充来使输入与输出的高和宽一致。最后我们将每条线路的输出在通道维上连结，并输入接下来的层中去。

十一、迁移学习

如果你有大量数据，你应该做的就是用开源的网络和它的权重，把这、所有的仪重当作初始化，然后训练整个网络。再次注意，如果这是一个1000节点的softmax，而你只有三个输出，你需要你自己的softmax输出层来输出你要的标签。

如果你有越多的标定的数据，可以训练越多的层。极端情况下，你可以用下载的权重只作为初始化，用它们来代替随机初始化，接着你可以用梯度下降训练，更新网络所有层的所有权重。

十二、第二周重要课后作业

编程作业：

参考链接：https://blog.csdn.net/u013733326/article/details/80250818

笑脸识别

下一次放假的时候，你决定和你的五个朋友一起度过一个星期。这是一个非常好的房子，在附近有很多事情要做，但最重要的好处是每个人在家里都会感到快乐，所以任何想进入房子的人都必须证明他们目前的幸福状态。

作为一个深度学习的专家，为了确保“快乐才开门”规则得到严格的应用，你将建立一个算法，它使用来自前门摄像头的图片来检查这个人是否快乐，只有在人高兴的时候，门才会打开。

你收集了你的朋友和你自己的照片，被前门的摄像头拍了下来。数据集已经标记好了。

代码：

import h5py
import time
import torch
import numpy as np
import torch.nn as nn
import matplotlib.pyplot as plt

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 加载数据集
def load_dataset():
    train_dataset = h5py.File('datasets/train_happy.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:])  # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:])  # your train set labels

    test_dataset = h5py.File('datasets/test_happy.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:])  # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:])  # your test set labels

    classes = np.array(test_dataset["list_classes"][:])  # the list of classes

    train_set_y_orig = train_set_y_orig.reshape((train_set_y_orig.shape[0], 1))
    test_set_y_orig = test_set_y_orig.reshape((test_set_y_orig.shape[0], 1))

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes


X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

print(X_train_orig.shape) # (600, 64, 64, 3),训练集600张，图像大小是64*64
print(Y_train_orig.shape) #  (600, 1)
print(X_test_orig.shape) # (150, 64, 64, 3)，测试集150张
print(Y_test_orig.shape)  # (150, 1)
print(classes.shape) # (2,) 一共2种类别，0：not happy; 1：happy

index = 5
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[index,:])))
#plt.show()

# 把尺寸(H x W x C)转为(C x H x W) ，即通道在最前面；归一化数据集
X_train = np.transpose(X_train_orig, (0, 3, 1, 2))/255          # 将维度转为(600, 3, 64, 64)
X_test = np.transpose(X_test_orig, (0, 3, 1, 2))/255            # 将维度转为(150, 3, 64, 64)
Y_train = Y_train_orig
Y_test = Y_test_orig

# 转成Tensor方便后面的训练（不然会数据类型报错）
X_train = torch.tensor(X_train, dtype=torch.float)
X_test = torch.tensor(X_test, dtype=torch.float)
Y_train = torch.tensor(Y_train, dtype=torch.float)
Y_test = torch.tensor(Y_test, dtype=torch.float)

print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)

# 构建网络结构（包含BN）
class ConvNet(nn.Module):
    def __init__(self):
        super(ConvNet, self).__init__()
        self.conv = nn.Sequential(

            nn.Conv2d(in_channels=3, out_channels=32, kernel_size=7, padding=3, stride=1), # in_channels, out_channels, kernel_size 二维卷积
            nn.BatchNorm2d(32), # 对输出按通道C批量规范化；γ和β可学习
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2), # kernel_size=2, stride=2；原函数就是'kernel_size', 'stride', 'padding'的顺序

        )
        self.fc = nn.Sequential(
            nn.Linear(32*32*32, 1),  # 16*3*3 向量长度为通道、高和宽的乘积
            nn.Sigmoid()   # S要大写；区别于torch.sigmoid()
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.reshape(img.shape[0], -1))  # 全连接层块会将小批量中每个样本变平
        return output


net = ConvNet()
print(net)


# 定义损失函数
#loss = nn.MSELoss()
loss = nn.BCELoss(reduction = 'sum')  # 0，1的交叉损失熵;返回loss的和

# 训练模型
def model(net, X_train, Y_train, device, lr=0.001, batch_size=32, num_epochs=1500,  print_loss=True, is_plot=True):

    net = net.to(device)
    print("training on ", device)
    # 定义优化器
    optimizer = torch.optim.Adam(net.parameters(), lr=lr, betas=(0.9, 0.999))

    # 将训练数据的特征和标签组合
    dataset = torch.utils.data.TensorDataset(X_train, Y_train)
    train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)

    train_l_list, train_acc_list = [], []
    for epoch in range(num_epochs):

        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            X = X.to(device)
            y = y.to(device)
            y_hat = net(X)#.squeeze(-1)
            ## 交叉熵损失函数中需要 .squeeze()用来将[batch_size,1]降维至[batch_size],.long用来将floatTensor转化为LongTensor，loss函数对类型有要求
            l = loss(y_hat, y)   #.sum()
            # print(y.shape,y_hat.shape)
            # print(l)

            # 梯度清零
            optimizer.zero_grad()

            l.backward()
            optimizer.step()

            train_l_sum += l.item()

            train_acc_sum += (torch.round(y_hat) == y).sum().item()
            # print(y_hat.argmax(dim=1).shape,y.shape)
            n += y.shape[0]
        train_l_list.append(train_l_sum / n)
        train_acc_list.append(train_acc_sum / n)
        if print_loss and ((epoch + 1) % 10 == 0):
            print('epoch %d, loss %.4f, train acc %.3f' % (epoch + 1, train_l_sum / n, train_acc_sum / n))

    # 画图展示
    if is_plot:
        epochs_list = range(1, num_epochs + 1)

        plt.subplot(211)
        plt.plot(epochs_list, train_acc_list, label='train acc', color='r')

        plt.title('Train acc')
        plt.xlabel('Epochs')
        plt.ylabel('Acc')
        plt.tight_layout()
        plt.legend()

        plt.subplot(212)
        plt.plot(epochs_list, train_l_list, label='train loss', color='b')
        plt.title('Train loss')
        plt.xlabel('Epochs')
        plt.ylabel('Loss')
        plt.tight_layout()
        plt.legend()
        plt.show()

    return train_l_list, train_acc_list

#开始时间
start_time = time.clock()
#开始训练
train_l_list, train_acc_list = model(net, X_train, Y_train, device, lr=0.0009, batch_size=64, num_epochs=100, print_loss=True, is_plot=True)
#结束时间
end_time = time.clock()
#计算时差
print("CPU的执行时间 = " + str(end_time - start_time) + " 秒" )


#计算分类准确率
def evaluate_accuracy(X_test, Y_test, net, device=None):


    if device is None and isinstance(net, torch.nn.Module):
        # 如果没指定device就使用net的device
        device = list(net.parameters())[0].device  # 未指定的话，就是cpu

    X_test = X_test.to(device)
    Y_test = Y_test.to(device)

    #print(net(X_test).shape,Y_test.shape)
    acc = (torch.round(net(X_test)) == Y_test).sum().item()
    acc = acc / X_test.shape[0]

    return acc

accuracy_train = evaluate_accuracy(X_train, Y_train, net)
print("训练集的准确率:", accuracy_train)

accuracy_test = evaluate_accuracy(X_test, Y_test, net)
print("测试集的准确率:", accuracy_test)

结果：

D:\Anaconda3\envs\pytorch\python.exe "D:/PyCharm files/deep learning/吴恩达/L4W2/L4W2_TRY.py"
(600, 64, 64, 3)
(600, 1)
(150, 64, 64, 3)
(150, 1)
(2,)
y = 1
torch.Size([600, 3, 64, 64])
torch.Size([150, 3, 64, 64])
torch.Size([600, 1])
torch.Size([150, 1])
ConvNet(
  (conv): Sequential(
    (0): Conv2d(3, 32, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3))
    (1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU()
    (3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (fc): Sequential(
    (0): Linear(in_features=32768, out_features=1, bias=True)
    (1): Sigmoid()
  )
)
training on  cuda
epoch 10, loss 0.0950, train acc 0.973
epoch 20, loss 0.0580, train acc 0.982
epoch 30, loss 0.0935, train acc 0.962
epoch 40, loss 0.0150, train acc 0.997
epoch 50, loss 0.0082, train acc 1.000
epoch 60, loss 0.0056, train acc 1.000
epoch 70, loss 0.0073, train acc 1.000
epoch 80, loss 0.0030, train acc 1.000
epoch 90, loss 0.0088, train acc 0.998
epoch 100, loss 0.0024, train acc 1.000
CPU的执行时间 = 40.573377799999996 秒
训练集的准确率: 1.0
测试集的准确率: 0.98

发现跟参考链接一样，很快就达到了较高的准确率。