前言

KNN算法是机器学习中较为简单的入门算法，其主要思想是选取k个与待预测点相近的数据，观察他们的类别，本着离谁近就更像谁的思路对于待预测点进行预测，本文将针对使用sklearn进行KNN算法的使用进行详解

数据预处理

在正式开始之前，我们先要进行数据预处理
数据预处理有两种常见的方式，MinMaxScaler和StandardScaler
MinMaxScaler: $X=\frac{X-max(X)}{max(X)-min(X)}$

StandardScaler: $X=\frac{X-mean(X)}{std(X)}$

from sklearn.preprocessing import MinMaxScaler, StandardScaler

minmaxscaler = MinMaxScaler() 
standardscaler = StandardScaler()

鸢尾花数据集

从sklearn.datasets中我们可以加载一些数据集，其中包含鸢尾花数据集

from sklearn import datasets
​
# 加载数据集
iris = datasets.load_iris()
X = iris.data[:,2:] # 这里为了画图方便，只取最后两个维度的信息
y = iris.target # 数据标签
X.shape, y.shape

((150, 2), (150,))

模型训练

从sklearn.neighbors我们引出KNeighborsClassifier分类器，直接调用KNN算法进行训练，我们在数据加载时选用sklearn.model_selection中提供的train_test_split来直接划分数据集

from sklearn.neighbors import KNeighborsClassifier  
from sklearn.model_selection import train_test_split 
​
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) 
# 以20%作为测试数据，随机数为42进行随机选取数据
​
X_train_std = standardscaler.fit_transform(X_train) # 数据预处理
X_test_std = standardscaler.fit_transform(X_test) # 数据预处理
​
# 实例化k值为3的knn模型，即n_neighbors=3，即选取最近的三个临近的点
knn_clf = KNeighborsClassifier(n_neighbors=3)  
knn_clf.fit(X_train_std, y_train)
knn_clf.score(X_test_std, y_test)

1.0

超参数选择

k值

对于KNN任务来讲，k值越小越容易过拟合，k值越大越容易欠拟合，所以对于k值的选用要特别注意
绘制子图
我们在这里编写了一个函数来绘制我们用于测试k值时需要画的图

def plot_decision_boundary(model,k, sub, X, y):
    # 用于画图的函数
    x0_min, x0_max = X[:,0].min()-1, X[:,0].max()+1 # 获取x0最小值和最大值
    x1_min, x1_max = X[:,1].min()-1, X[:,0].max()+1 # 获取x1最小值和最大值
    x0, x1 = np.meshgrid(np.linspace(x0_min, x0_max, 100), np.linspace(x1_min, x1_max, 100))  # 以x0和x1的最小值和最大值生成100个二维网格数据
    Z = model.predict(np.c_[x0.ravel(), x1.ravel()]) # 对生成的数据进行预测
    Z = Z.reshape(x0.shape)
    
    # plt.contourf是用来绘制等高线的函数，给定二维坐标和高度值可以画出等高线，x0, x1为二维坐标，Z为高度
    plt.subplot(sub[0], sub[1], sub[2])  # 绘制子图
    plt.contourf(x0, x1, Z, cmap=plt.cm.Spectral) # 预测数据的等高线
    plt.ylabel("x1")
    plt.xlabel("x0")
    plt.xticks([])
    plt.yticks([])
    plt.title('k={:d}'.format(k))
    plt.scatter(X[:,0], X[:,1],c=np.squeeze(y))  # 原数据

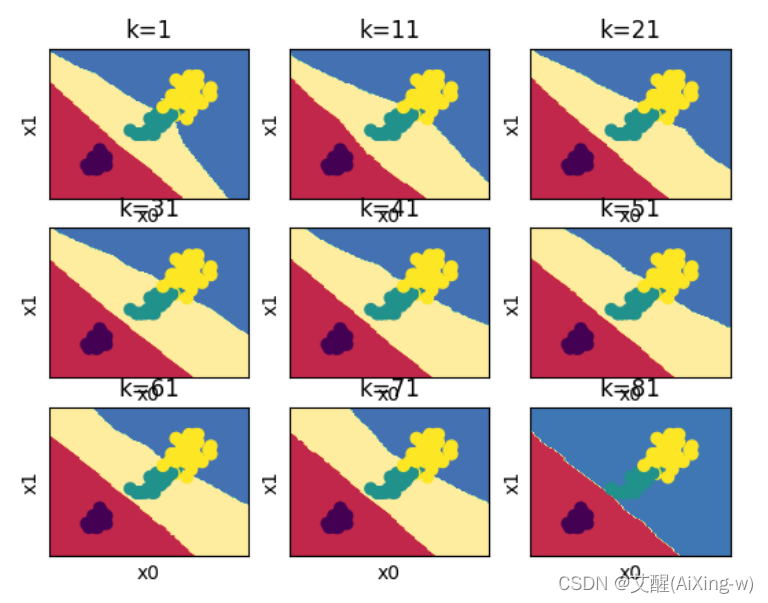
选择不同的k值并画图

for k in range(1, 90, 10):
    knn_clf = KNeighborsClassifier(n_neighbors=k)  # 选择不同的k值
    knn_clf.fit(X_train_std, y_train)
    plot_decision_boundary(knn_clf, k, (3, 3, k // 10+1), X_train_std, y_train)
plt.show()

其他参数

我们可以通过help来获取knn分类器的其他参数

help(knn_clf) # 查看KNN分类器的参数

可以看到Parameters下全是参数以及可选范围的介绍，我们随便选用几个进行尝试

网格搜索

由于每个参数及其组合我们一个个的去试效率太低，所以我们使用网格搜索来进行，我们在前面使用help已经知道了分类器的参数以及可选的值了，这里我们只需要先设置一个由字典组成的列表并将他和模型一起传到GridSearchCV的实例化中再次进行GridSearchCV的训练就可以得到最佳参数了，在由字典组成的列表中，每一个字典是选用不同的参数组合，字典的key是参数名，字典的value是要进行网格搜索的值，这里的值一定要满足help中规定的值

from sklearn.model_selection import GridSearchCV
​
# 使用网格搜索寻找最佳参数
param_grid=[
    {
        'weights':['uniform'],
        'n_neighbors':list(range(1, 11))
    },
    {
        'weights':['distance'],
        'n_neighbors':list(range(1, 11)),
        'p':list(range(1, 6))
    }
]
​
knn_clf = KNeighborsClassifier()
grid_search = GridSearchCV(knn_clf, param_grid)
grid_search.fit(X_train, y_train)
GridSearchCV

最佳准确率

grid_search.best_score_  # 最好的准确率是0.9583333333333334

0.9583333333333334

最佳参数

grid_search.best_params_  # 最好准确率对应的参数是{'n_neighbors': 1, 'weights': 'uniform'}

{‘n_neighbors’: 1, ‘weights’: ‘uniform’}