👨🎓 个人主页: 研学社的博客
💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥
🏆 博主优势: 🌞 🌞 🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳ 座右铭:行百里者,半于九十。
📋 📋 📋 本文目录如下: 🎁 🎁 🎁
目录
💥1 概述
📚2 运行结果
🎉3 文献来源
🌈4 Matlab代码实现
💥1 概述

编辑
本文提出了一种新的基于种群的技术,称为粪甲虫优化器(DBO)算法,其灵感来自于粪甲虫的滚球、跳舞、觅食、偷窃和繁殖行为。新提出的DBO算法同时考虑了全局探索和局部开发,从而具有快速收敛速度和令人满意的解精度的特点。使用一系列众所周知的数学测试函数(包括23个基准函数和29个CEC-BC-2017测试函数)来评估DBO算法的搜索能力。从仿真结果中可以观察到,DBO算法在收敛速度、解的精度和稳定性方面与最先进的优化方法相比具有实质上的竞争性能。
详细文章讲解见第四部分。
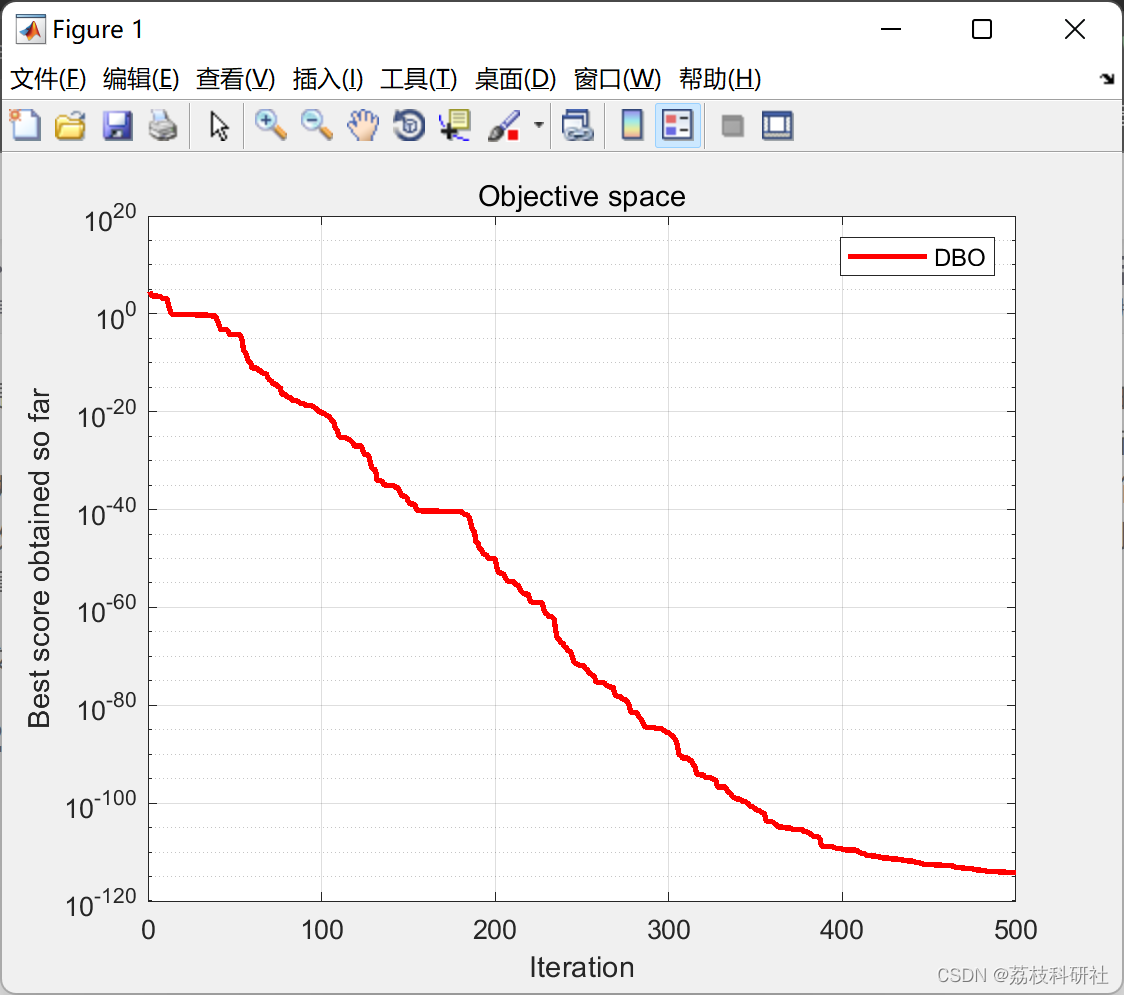
📚2 运行结果

部分代码:
function [fMin , bestX, Convergence_curve ] = DBO(pop, M,c,d,dim,fobj )
P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( pop * P_percent ); % The population size of the producers
lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
for i = 1 : pop
x( i, : ) = lb + (ub - lb) .* rand( 1, dim );
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x;
XX=pX;
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
% Start updating the solutions.
for t = 1 : M
[fmax,B]=max(fit);
worse= x(B,:);
r2=rand(1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1 : pNum
if(r2<0.9)
r1=rand(1);
a=rand(1,1);
if (a>0.1)
a=1;
else
a=-1;
end
x( i , : ) = pX( i , :)+0.3*abs(pX(i , : )-worse)+a*0.1*(XX( i , :)); % Equation (1)
else
aaa= randperm(180,1);
if ( aaa==0 ||aaa==90 ||aaa==180 )
x( i , : ) = pX( i , :);
end
theta= aaa*pi/180;
x( i , : ) = pX( i , :)+tan(theta).*abs(pX(i , : )-XX( i , :)); % Equation (2)
end
x( i , : ) = Bounds( x(i , : ), lb, ub );
fit( i ) = fobj( x(i , : ) );
end
[ fMMin, bestII ] = min( fit ); % fMin denotes the current optimum fitness value
bestXX = x( bestII, : ); % bestXX denotes the current optimum position
R=1-t/M; %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Xnew1 = bestXX.*(1-R);
Xnew2 =bestXX.*(1+R); %%% Equation (3)
Xnew1= Bounds( Xnew1, lb, ub );
Xnew2 = Bounds( Xnew2, lb, ub );
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Xnew11 = bestX.*(1-R);
Xnew22 =bestX.*(1+R); %%% Equation (5)
Xnew11= Bounds( Xnew11, lb, ub );
Xnew22 = Bounds( Xnew22, lb, ub );
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = ( pNum + 1 ) :12 % Equation (4)
x( i, : )=bestXX+((rand(1,dim)).*(pX( i , : )-Xnew1)+(rand(1,dim)).*(pX( i , : )-Xnew2));
x(i, : ) = Bounds( x(i, : ), Xnew1, Xnew2 );
fit(i ) = fobj( x(i,:) ) ;
end
for i = 13: 19 % Equation (6)
x( i, : )=pX( i , : )+((randn(1)).*(pX( i , : )-Xnew11)+((rand(1,dim)).*(pX( i , : )-Xnew22)));
x(i, : ) = Bounds( x(i, : ),lb, ub);
fit(i ) = fobj( x(i,:) ) ;
end
for j = 20 : pop % Equation (7)
x( j,: )=bestX+randn(1,dim).*((abs(( pX(j,: )-bestXX)))+(abs(( pX(j,: )-bestX))))./2;
x(j, : ) = Bounds( x(j, : ), lb, ub );
fit(j ) = fobj( x(j,:) ) ;
end
% Update the individual's best fitness vlaue and the global best fitness value
XX=pX;
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
if( pFit( i ) < fMin )
% fMin= pFit( i );
fMin= pFit( i );
bestX = pX( i, : );
% a(i)=fMin;
end
end
Convergence_curve(t)=fMin;
end
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
temp = s;
I = temp < Lb;
temp(I) = Lb(I);
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;
function S = Boundss( SS, LLb, UUb)
% Apply the lower bound vector
temp = SS;
I = temp < LLb;
temp(I) = LLb(I);
% Apply the upper bound vector
J = temp > UUb;
temp(J) = UUb(J);
% Update this new move
S = temp;
%---------------------------------------------------------------------------------------------------------------------------
🎉3 文献来源
部分理论来源于网络,如有侵权请联系删除。