来源:力扣(LeetCode)
描述:
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:9
示例 2:
输入:grid = [[1,1,0,0]]
输出:1
提示:
- 1 <= grid.length <= 100
- 1 <= grid[0].length <= 100
- grid[i][j] 为 0 或 1
方法:动态规划
思路与算法
我们假设以 (x, y) 为右下方顶点的最大的正方形边长为 l,此时正方形的四个顶点分别为 (x − l + 1, y − l + 1), (x, y − l + 1), (x − l + 1, y), (x, y),此时需要保证正方形的四条边上的数字均为 1。我们设 left[x][y] 表示以 (x, y) 为起点左侧连续 1 的最大数目,right[x][y] 表示以 (x, y) 为起点右侧连续 1 的最大数目,up[x][y] 表示从 (x, y) 为起点上方连续 1 的最大数目,down[x][y] 表示以 (x, y) 为起点下方连续 1 的最大数目。此时正方形的四条边中以四个顶点为起点的连续 1 的数目分别为:上侧边中以 (x − l + 1, y − l + 1) 为起点连续 1 数目为 right[x − l + 1][y − l + 1],左侧边中以 (x − l + 1, y − l + 1) 为起点连续 1 的数目为 down[x − l + 1][y − l + 1],右侧边中以 (x, y) 为起点连续 1 的数目为 up[x][y],下侧边中以 (x,y) 为起点连续 1 的数目为 left[x][y]。
如果连续 1 的数目大于等于 l,则构成一条「合法」的边,如果正方形的四条边均「合法」,此时一定可以构成边界全为 1 且边长为 l 的正方形。

我们只需要求出以 (x, y) 为起点四个方向上连续 1 的数目,枚举边长 l 即可求出以 (x, y) 为右下顶点构成的边界为 1 的最大正方形,此时我们可以求出矩阵中边界为 1 的最大正方形。
本题即转换为求矩阵中任意位置 (x, y) 为起点上下左右四个方向连续 1 的最大数目,此时可以利用动态规划:
-
如果当前 grid[x][x] = 0 此时,四个方向的连续 1 的长度均为 0;
-
如果当前 grid[x][x] = 1 此时,四个方向的连续 1 的最大数目分别等于四个方向上前一个位置的最大数目加 1,计算公式如下:
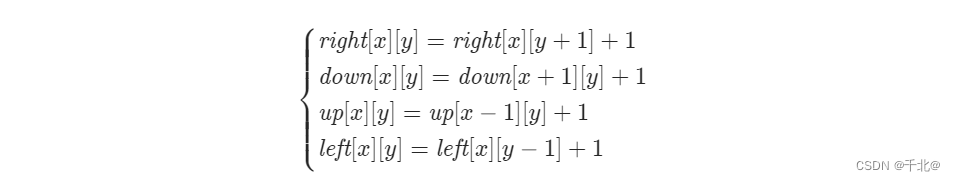
在实际计算过程中我们可以进行优化,不必全部计算出四个方向上的最大连续 1 的数目,可以进行如下优化:
只需要求出每个位置 (x, y) 为起点左侧连续 1 的最大数目 left[x][y] 与上方连续 1 的最大数目 up[x][y] 即可。假设当前正方形的边长为 l,此时只需检测 up[x][y], left[x][y], left[x − l + 1][y], up[x][y − l + 1] 是否均满足大于等于 l 即可检测正方形的合法性。
枚举正方形的边长时可以从大到小进行枚举,我们已经知道以 (x, y) 为起点左侧连续 1 的最大数目 left[x][y] 与上方连续 1 的最大数目 up[x][y],此时能够成正方形的边长的最大值一定不会超过二者中的最小值 min(left[x][y], up[x][y]),从大到小枚举直到可以构成“合法”的正方形即可。
代码:
class Solution {
public:
int largest1BorderedSquare(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> left(m + 1, vector<int>(n + 1));
vector<vector<int>> up(m + 1, vector<int>(n + 1));
int maxBorder = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (grid[i - 1][j - 1] == 1) {
left[i][j] = left[i][j - 1] + 1;
up[i][j] = up[i - 1][j] + 1;
int border = min(left[i][j], up[i][j]);
while (left[i - border + 1][j] < border || up[i][j - border + 1] < border) {
border--;
}
maxBorder = max(maxBorder, border);
}
}
}
return maxBorder * maxBorder;
}
};
执行用时:8 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:11.4 MB, 在所有 C++ 提交中击败了54.29%的用户
复杂度分析
时间复杂度:O(m × n × min(m, n)),其中 m 表示矩阵的行数,n 表示矩阵的列数。
空间复杂度:O(m × n),其中 m 表示矩阵的行数,n 表示矩阵的列数。需要保存矩阵中每个位置的最长连续 1 的数目,需要的空间为 O(m × n)。
author:LeetCode-Solution