前言
本文是博主自己在准备学校数据结构考试时的总结,各个知识点都贴有对应的详细讲解文章以供大家参考;
当然文中还有许许多多的截图,这些是博主对主要内容的摘取,对于那些基础较好的同学可以直接看截图,减少跳转对应文章浏览全文的时间,
感谢本文引用文章的各位大佬,希望可以让更多同学看到这些优质文章并且得以受益。
1.KMP算法
求next数组(存储的是序号):
- 对数据进行编号,从1开始;
- 前两个必定为 0,1;
- 往后字符:找它的前一个和前一个的next数组对应序号的字符进行比较;
- 若不相同,则继续找前一个的next所对应的next,若相等,则所需位的next为当前比较字符的next值加1;
- 若果到第一个都没有匹配,则next为1。
本部分截图来源:讲解例题
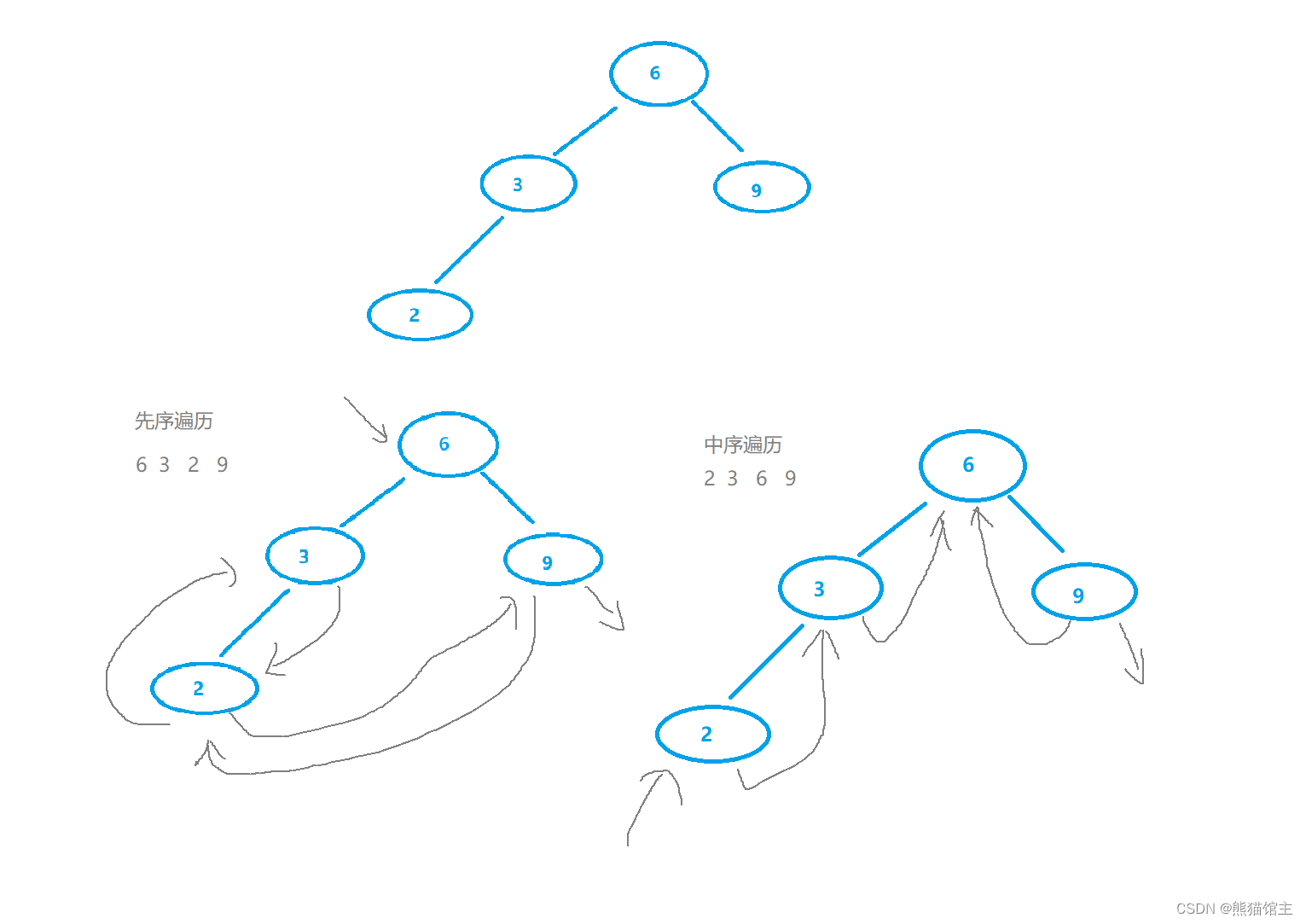
2.二叉树
堆
知识点参考文章:堆与二叉树
二叉排序树/二叉搜索树/二叉查找树
AVL树
自平衡二叉查找树
补充:二叉线索树
任然采用左右孩子的存储形式,
当该节点的左孩子为空时可以指向它的前驱节点,
当该节点的右孩子为空时可以指向它的后继节点。
二叉线索树根据遍历顺序的不同会有所改变。
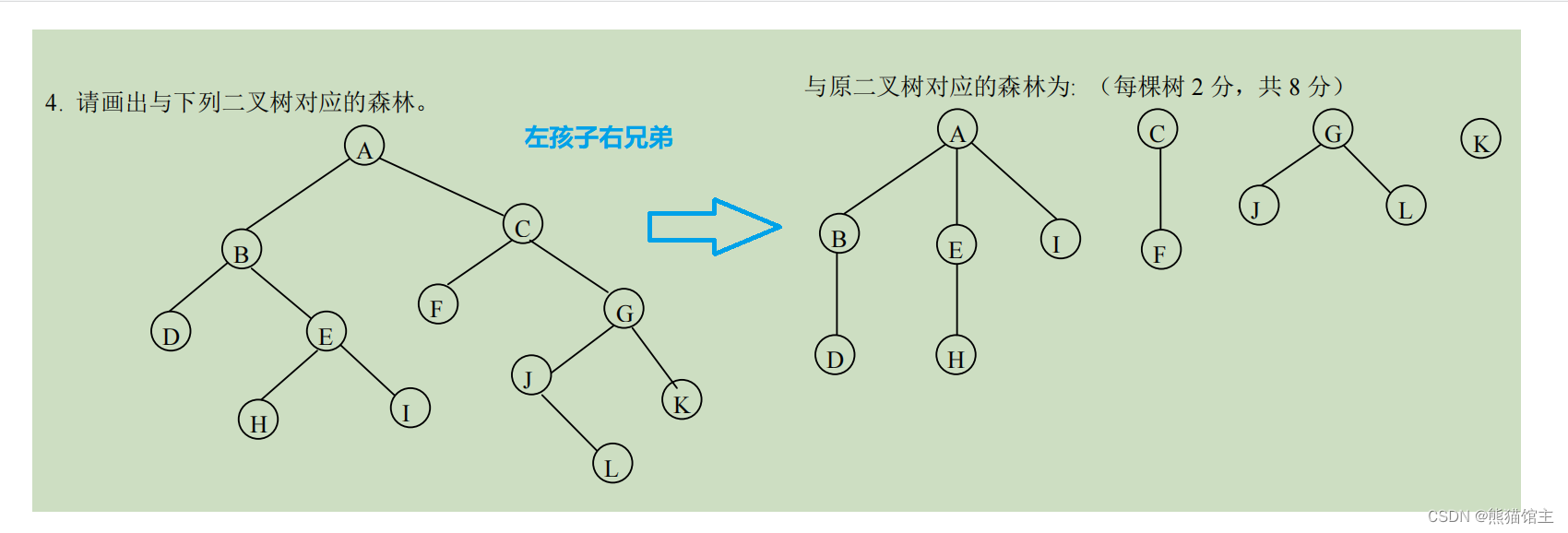
二叉树和森林的转换
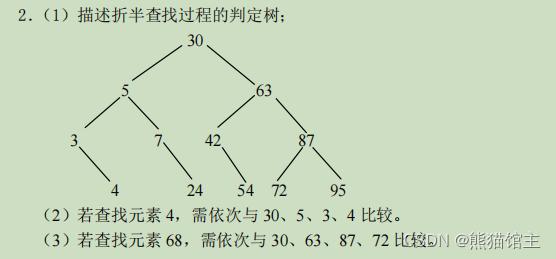
3.折半查找
判定树:查找数据的路程图。
4.哈夫曼树
举个栗子:
5. 排序
一轮希尔排序:eg:步长为4的时候进行一次完整的插入排序,而非只进行一轮插入排序。
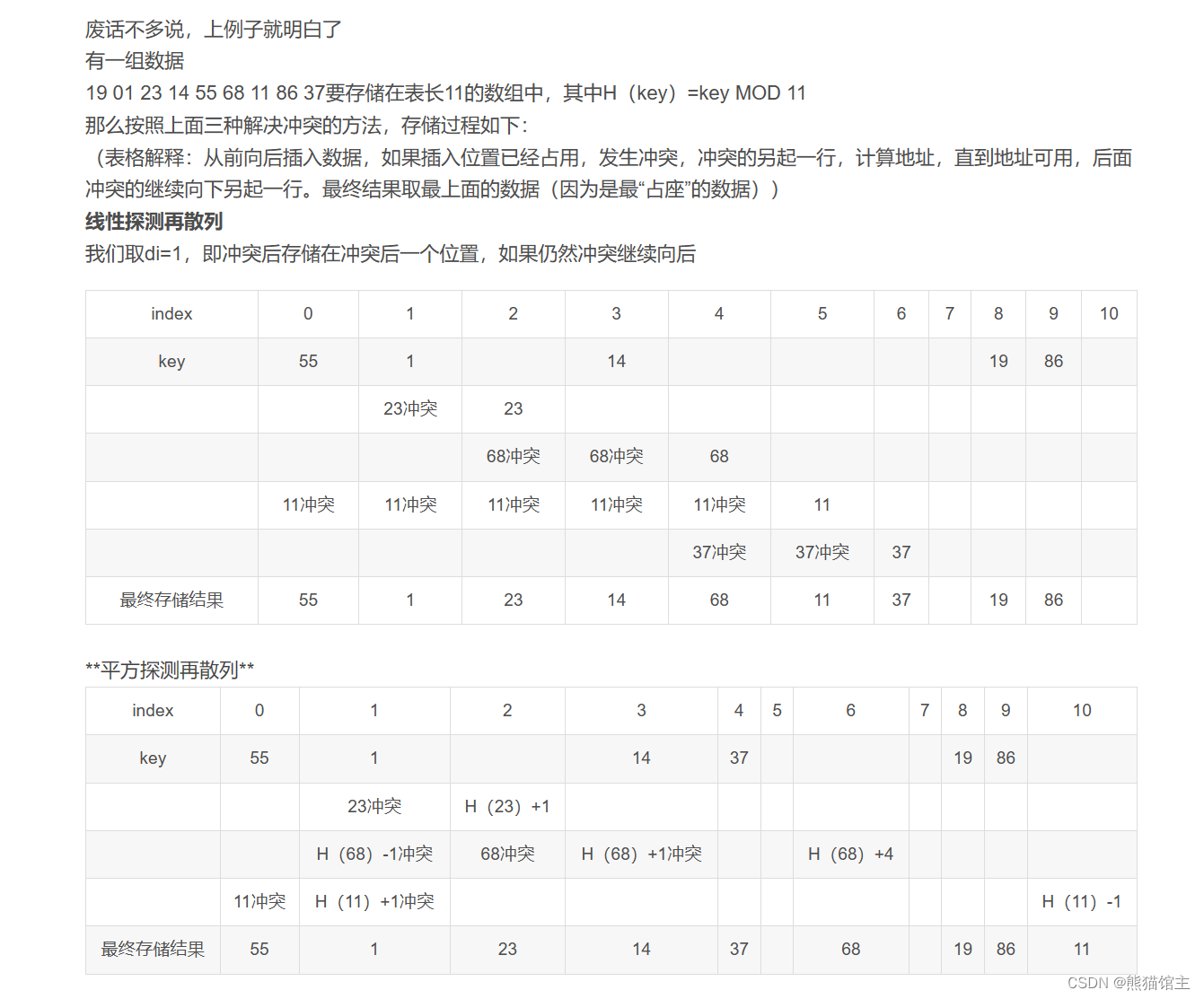
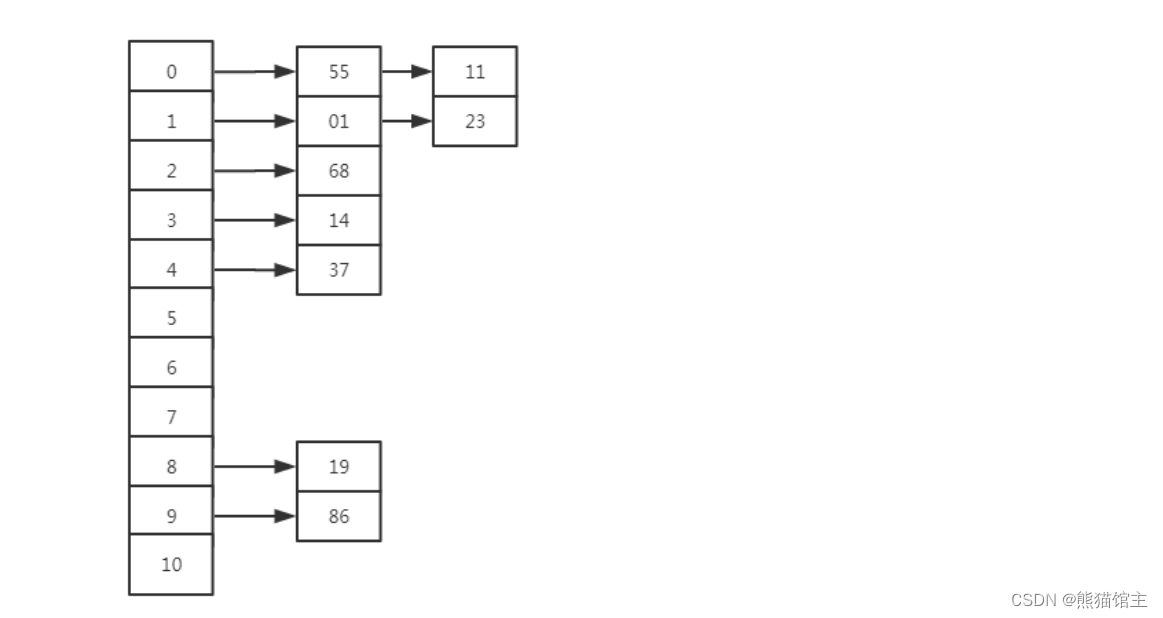
6.哈希表
重点知识:哈希冲突 和 平均查找时间
哈希冲突
哈希冲突优质文章:解决哈希冲突的四种方法
截图来源:数据结构 哈希表
平均查找时间
如果查找每个元素的概率相同,则查找各个元素的平均查找时间(或者平均查找次数)
举例:链地址法:
各个节点在对应链表上的位置的累加和。
7.广义表
表头、表尾
截图来源文章:广义表的表头和表尾是什么?
长度、深度
长度:包含数据元素(原子或子表)个数;
深度:最多嵌套括号层数。
截图来源文章:广义表的广度(长度)和深度的计算
8.图
图中顶点与边的关系
上方截图来自:图中结点、边和度之间的关系总结
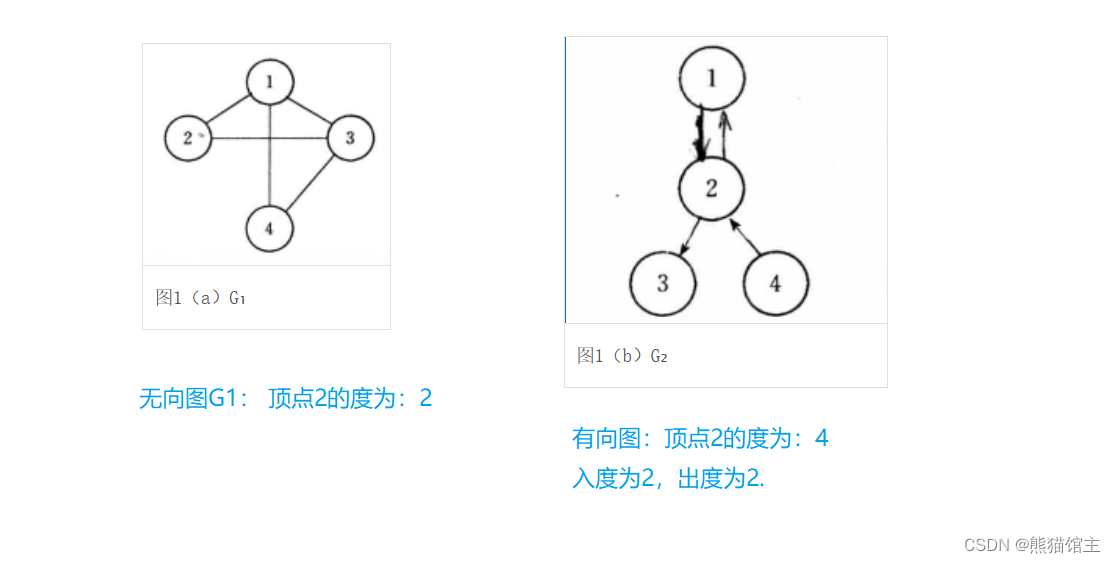
顶点的度
无向图:顶点的度为顶点具有边的条数;
有向图:分为入度和出度,有向图顶点的度为入度和出度之和。
其实都是顶点具有边的条数。
连通与强连通
连通讲的是:无向图
强连通讲的是:有向图
截图来源:强连通分量
关键路径
关键路径:从源点到终点的最长路径。
优质文章:数据结构 – 关键路径详解
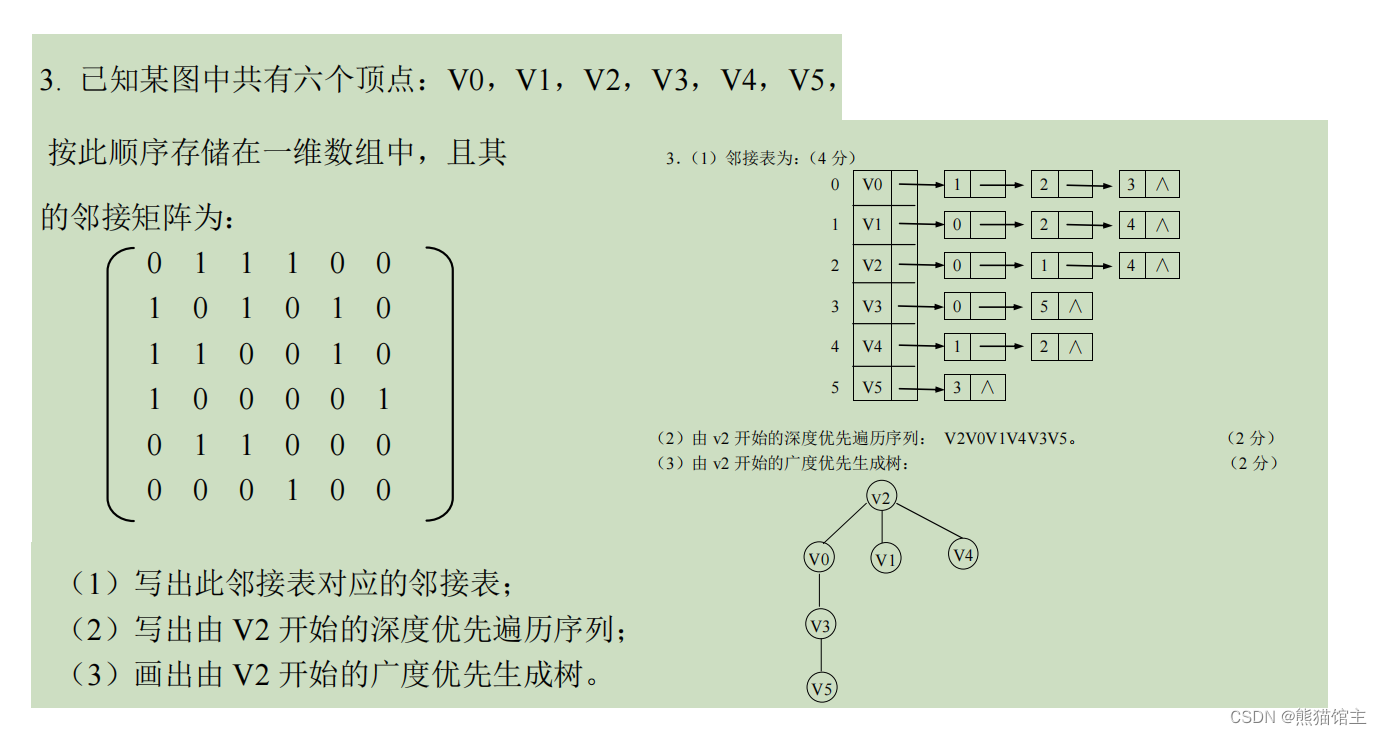
9.邻接矩阵与邻接表
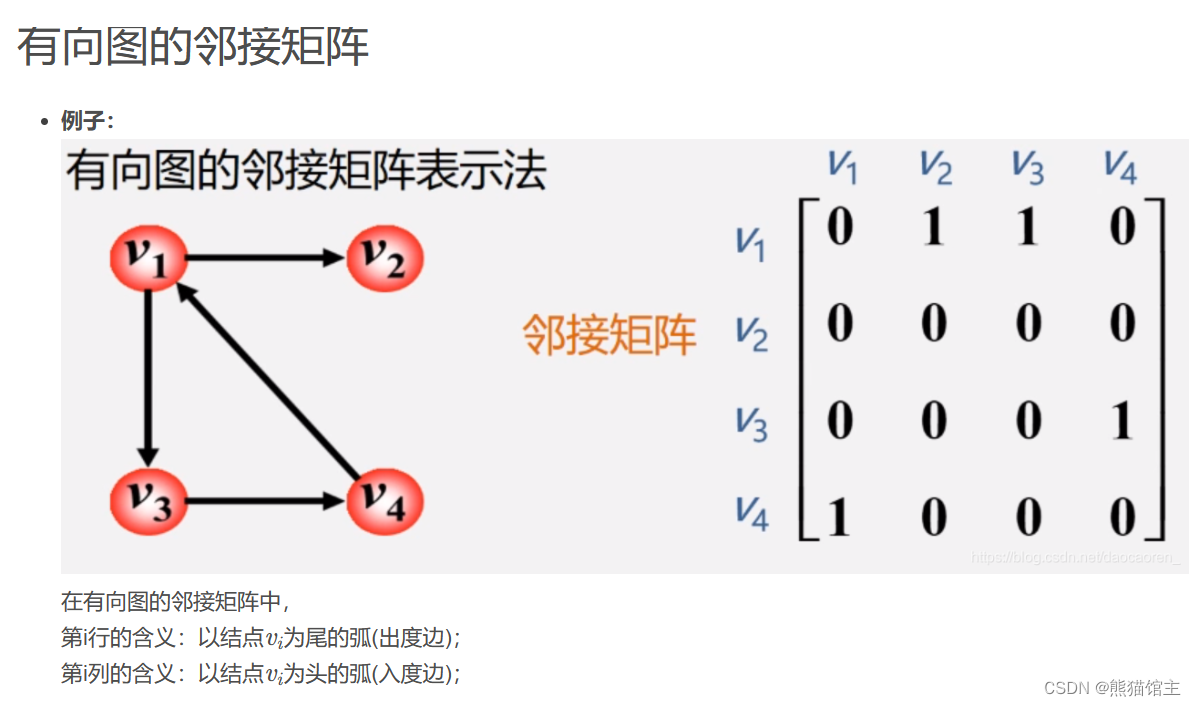
邻接矩阵
对于图 G=(V, E) 而言,其中 V 表示顶点集合,E 表示边集合。
- 申请一个大小为O(n^2)的二维数组,来存放节点之间的连通关系以及权值(不需要存放权值的直接使用bool值表示);
- 无向图的邻接矩阵是关于主对角线对称的,因此可以只存储一半关系来节省空间;
行表示该节点的出度,
列表示该节点的入度。
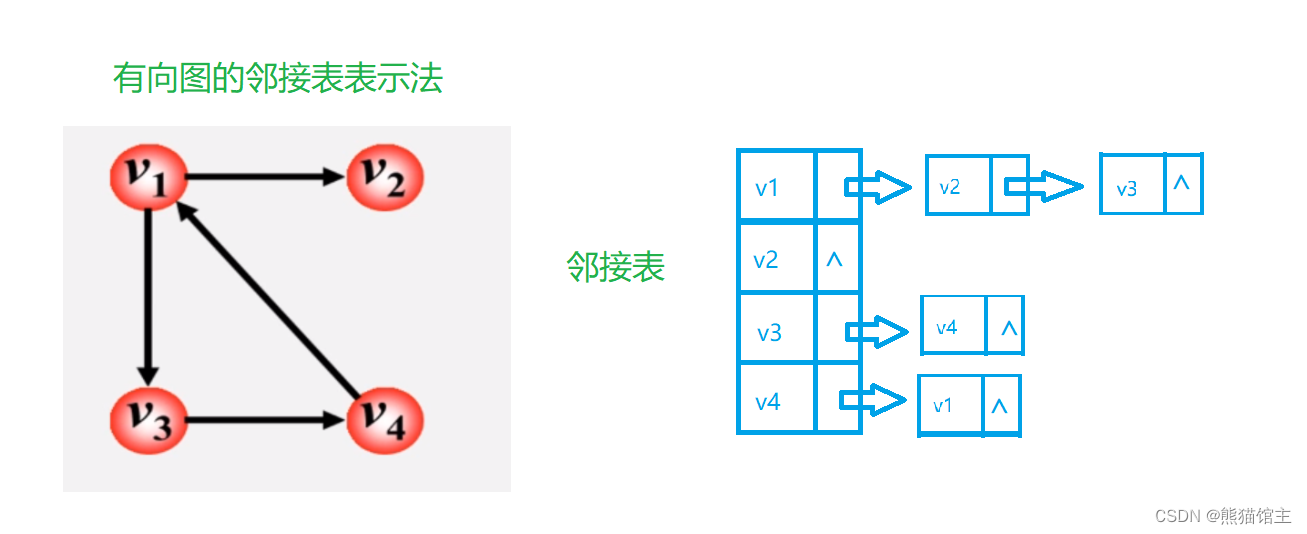
邻接表
使用邻接表需要申请[V]个列表
- 每个列表存储所有从顶点出发的所以相邻顶点,列表总存储顶点数为[E];
- 无向图的列表总存储顶点数为2*[E]。
两者的比较
根据邻接表和邻接矩阵的结构特性可知,当图为稀疏图、顶点较多,即图结构比较大时,更适宜选择邻接表作为存储结构。当图为稠密图、顶点较少时,或者不需要记录图中边的权值时,使用邻接矩阵作为存储结构较为合适。
深度优先遍历 和 广度优先遍历
遍历方法:
例题
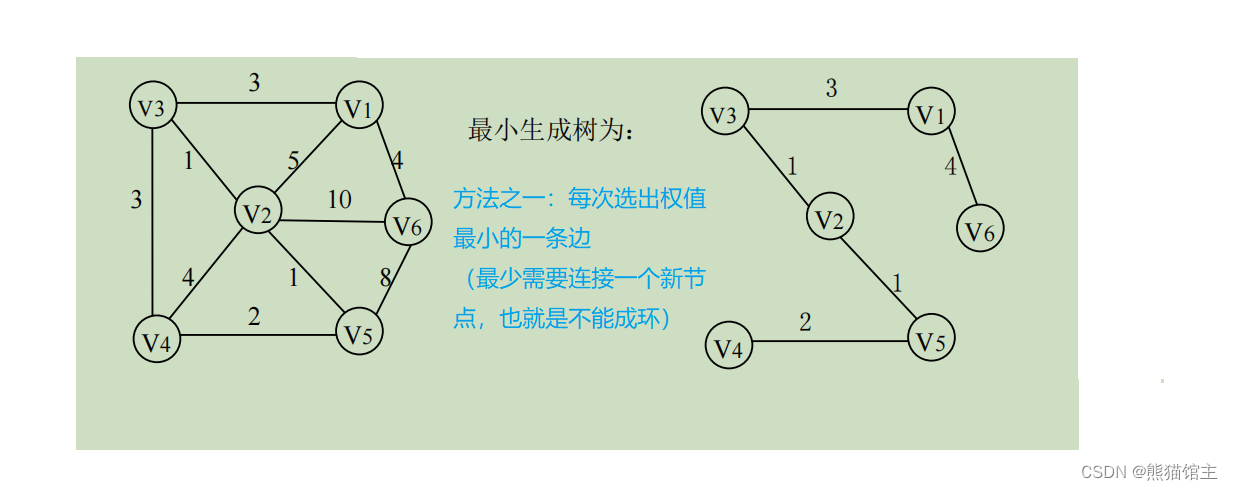
最小生成树
最小生成树概念:带权值的图中,连接所有顶点后花费最小的生成树。
注意:不同算法得到的最小生成树可能相同也可能不同。
优质文章:数据结构–最小生成树详解
10.拓扑排序
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
注意:只有有向无环图才有拓扑排序。