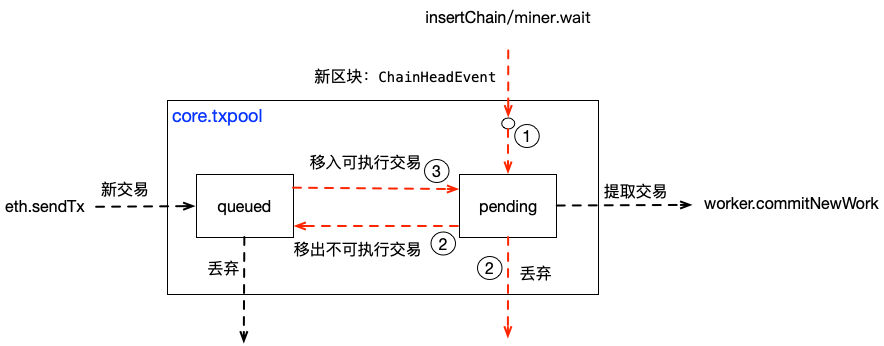
论文地址：
Reinforcement Learning Based Approach for Multi-Vehicle Platooning Problem with Nonlinear Dynamic Behavior

摘要

协同智能交通系统领域的最新研究方向之一是车辆编队。研究人员专注于通过传统控制策略以及最先进的深度强化学习 (RL) 方法解决自动驾驶车辆控制的各种方法。在这项研究中，除了提出基于 RL 的最优间隙控制器之外，还重新引入了详细的非线性动力车辆模型，这通过具有深度确定性策略梯度算法的 actor critic 策略进行了证明。生成的智能体针对可变速度和可变间隙侵略性场景进行模拟，并与模型预测控制 (MPC) 性能进行比较。结果表明，准确性和学习时间之间存在权衡。但是，两个控制器都具有接近最佳的性能。

前言

存在的问题

从上述文献来看，在利用 RL 作为队列中动态车辆模型的控制器方面存在研究空白。一些研究人员使用传统控制器来解决队列问题。

此外，[12] 提到了各种应用基于深度 RL 的控制器的研究，这些研究仅考虑点质量运动学模型，而没有加速延迟动力学的影响。

其他研究人员专注于在单个车辆或跟车问题上使用基于 RL 的控制器，而没有考虑相对距离控制。如以下各节所述，本研究填补了上述研究空白。

问题描述

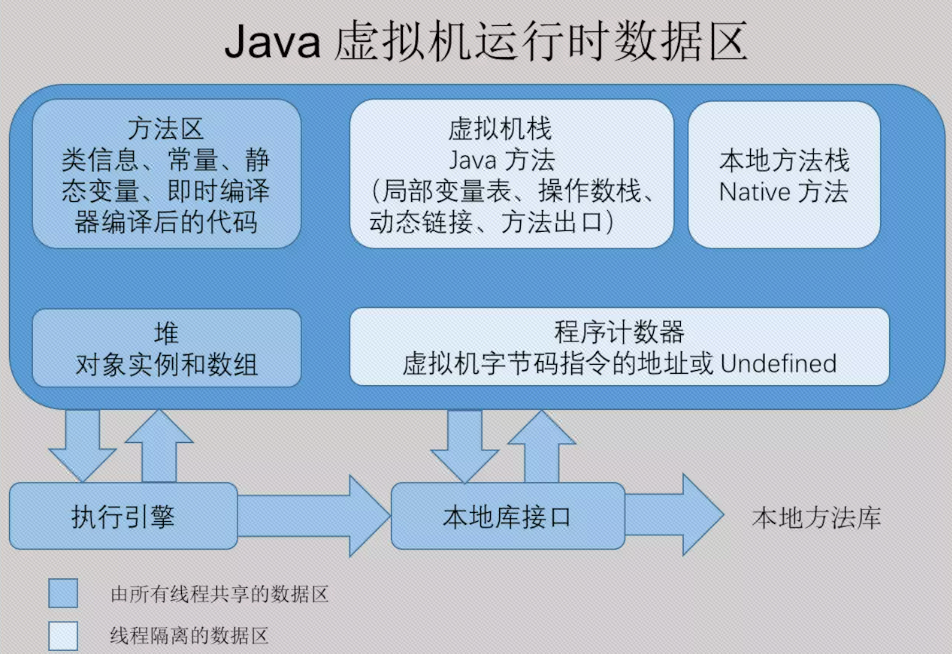
车辆动力学模型

在这项研究中，所考虑的队列配置由异构车辆组成，即车辆的质量、长度或最重要的是车辆的阻力系数可能不同。

此外，该队列有四辆车、一辆领队和任意数量的随车，其中领队位于第一个位置。描述运动曲线的领导者状态是 $\dot{x_0}$ 和$\ddot{x_0}$，分别代表领导者的速度和加速度。此外，两辆车之间的距离 $d_g^{(i)}$是本车在位置 $i$ 的前保险杠与前车在位置 $i-1$ 的后保险杠之间的距离。

此外，假定领导者遵循仅为其预定义的速度轨迹。其他车辆的目标是跟随前面车辆的轨迹，同时保持定义的相对距离$d_g^{(i)}$ 。因此，假设存在完美的车对车 (V2V) 通信，即所有车辆都可以观察到前车的状态，并且第$i$辆车的位置 $x(i)$ 是从车辆的质心测量的。对于本节的其余部分，将对用于表示车辆行为的模型进行进一步调查。

然而，阻力进一步研究。由于这项研究的目的是调查队列中的行为，因此更现实的做法是考虑由于队列配置而减少作用在自我车辆上的阻力的影响。在上述原因下，单个队列成员的动力学由方程式 1 建模。
$$\begin{array}{c}\begin{array}{r}\ddot{x}=\frac{T_t-T_{br}-(F_d+F_r+F_g)\cdot R}{m\cdot R+\frac{I_w}{R}}\end{array}\end{array}$$
其中 $T_t$ 是由发动机产生并导致车辆向前运动的牵引扭矩，$T_{b}r$ 是由制动系统产生的用于控制车辆减速的扭矩，$F_d$、$F_r$ 和 $F_g$ 是阻力、滚动阻力和重力。阻力乘以减阻比，该减阻比模拟前车对本车阻力的影响，如 [15] 中所示。最后，$m、R和I_w$ 分别是车辆质量、车轮半径和车轮转动惯量。

状态空间模型

控制器智能体只观察两辆连续车辆之间的差距、速度和加速度的误差。对于领导者，设计了一个单独的速度控制器智能体来维持设定的速度 ${\dot{x}}_{ref}^{(0)}$ 。队列中所有车辆的车辆模型与第 3 节中导出的相同。此外，控制器用于控制队列的车辆间距。

说明拓扑是TPF双前车跟随式。

奖励设置

领航车的奖励

$$\begin{array}{c}{R}_{l,t}=-(u_{t-1}^2+0.05{\dot{u}}_{t-1}^2+0.1e_{vl,t}^2)+Q_{l,t}\end{array}$$

其中$ u_{t−1}$ 是前一时刻的控制力（加速度）$\dot{u_{t-1}}$是前一时刻的控制力（加速度）的导数。$e_{vl,t}$是设定参考速度与当前领导者速度 $v_{ref}-\dot{x_0}$ 之间的速度误差，$Q_{l,t}$是基于逻辑方程的正奖励：

$$Q_{l,t}=\left|e_{vl,t}\right|\le {\vartheta }_v\wedge t\ge \tau$$
其中${\vartheta }_v$是可接受的速度误差容差的阈值，$\tau$是奖励存在的阈值时间。

奖励负数部分的平方是为了说明所描述术语中的正值或负值。第一项说明加速度的最小化，而第二项说明加速度的变化。因此，最大限度地减少控制工作中的抖动并确保信号的平滑度。第三项消除了速度误差以实现控制器的预期行为。 Q 部分是在设定点周围给予智能体正奖励，以抑制控制超调，而不是将控制器收紧到严格的值。延迟条件对于确保控制器仅在实际处于正确速度时才收到正奖励非常重要，并防止因初始领导者速度与设定速度接近零误差而产生的任何假正奖励。

跟随车辆的奖励

$$R_{f,t}=-\left(u_{t-1}^2+0.05{\dot{u}}_{t-1}^2+{\left(\frac{1}{v_{max}}{e}_{vf,t}\right)}^2+{\left(\frac{1}{d_{gmax}}{e}_{g,t}\right)}^2\right)+Q_{f,t}$$

它具有与等式（2）中相同的控制努力参数。然而，$e_{vf,t}$是当前速度与前车速度之间的速度误差 $v_i-v_{i-1}$，而 $e_{g,t} $是间隙误差 ${gap}_{desired}-d_g^i$，$Q_{f,t}$是正奖励基于逻辑等式：

$$Q_{f,t}=|e_{v,t}|\le {\vartheta }_v\wedge |e_{g,t}|\le {\vartheta }_g\wedge t\ge \tau$$

等式 ($2$) 和 (3) 中的项的相同原因用于等式 (4) 和 (5) 中，增加了间隙项中的误差以消除实现所需控制器的误差。等式 (4) 中速度和间隙误差的增益用于对值进行归一化。因此，智能体可以比非标准化函数更容易满足多目标奖励函数。

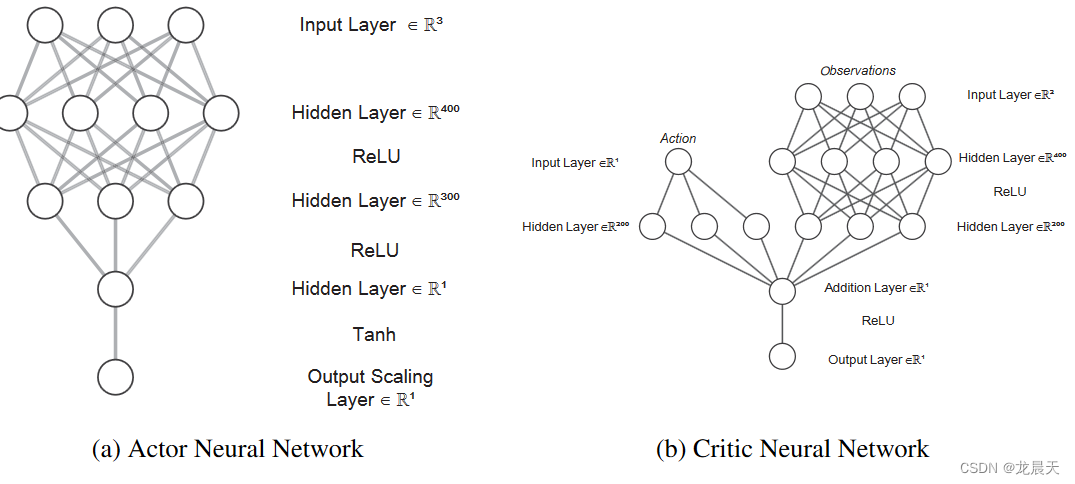
网络结构

演员网络具有三个完全连接的隐藏层，分别具有 400、300 和一个神经元，而对于评论家网络，动作路径具有一个具有 300 个神经元的隐藏层。状态路径有两个隐藏层，分别有 400、300 个神经元。两条路径都通过加法层合并到输出层。 RL 模型以 0.1 秒的采样时间运行，奖励折扣因子为 0.99，噪声模型方差为 0.6。对于训练过程，小批量大小为 128，而演员和评论家网络的学习率分别为 10−4 和 10−3。

实验结果

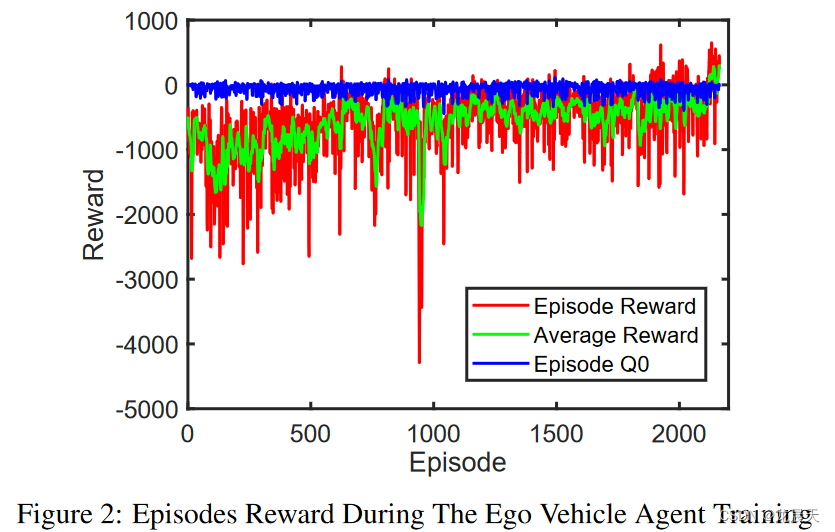
自我车辆控制器的训练进行了 2163 集，总步数为 973,186，持续了大约 9.5 小时。如图 2 所示，基于公式 4 的最终平均奖励为 326.8。车辆速度和位置的初始条件在每一集开始前随机更改，以确保智能体在任何给定的现实场景中的可靠性并防止模型对某些场景的过度拟合。因此，每一集都有不同的初始间隙误差和不同的初始速度误差。

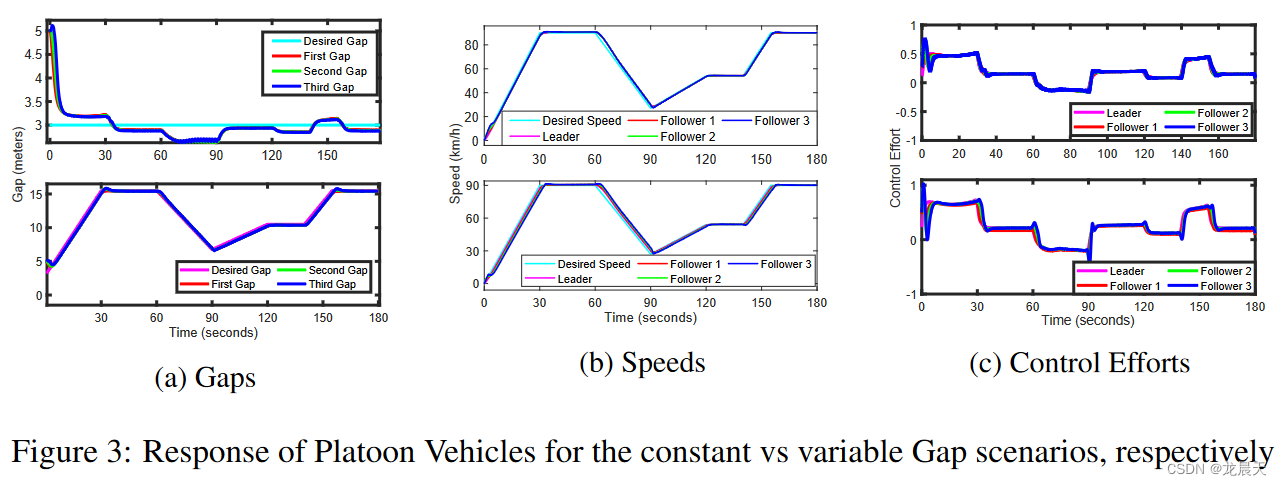
关于恒定距离间隙场景，智能体以可接受的误差容限 ($$\sim |e_{g,t}|\le 0.3$$) 实现了所需的间隙，这满足了等式 5 中的奖励函数。稳定时间非常接近 MPC 的响应，即[13] 中三个控制器中最快的一个。整体响应类似于 MPC，如图 5 所示，这是有道理的，可以从 RL 和 MPC 都试图解决优化问题以分别找到最优策略 π* 或控制律 u* 的事实中推导出来.此外，据观察，对于预定义的速度轨迹，控制工作是平稳且现实的。间隙控制器已证明能够在目标奖励函数中指定的公差范围内以令人满意的方式处理简单和激进的场景。

可变间隙参考轨迹是根据速度轨迹设计的，其中所需间隙等于 3 米的安全距离加上一个定时间隙，其幅度为速度的一半（以米/秒为单位）。此外，智能体的响应以令人满意的方式对具有平滑速度轨迹的间隙变化做出快速反应，如图 3b 所示。必须指出的是，在间隙变化的部分，跟随器的速度相对于参考速度存在恒定的偏移，从而导致间隙的增加或减小。

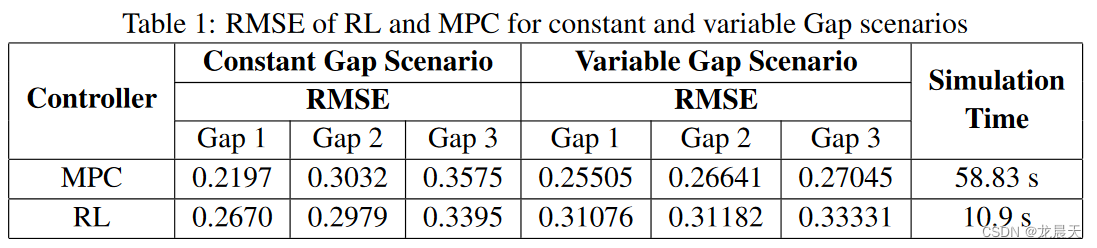
如表 1 所示，RL 智能体为之前在 [13] 中讨论的控制器提供了类似的均方根误差 (RMSE)。然而，就计算时间而言，RL 智能体的模拟速度明显快于之前提出的最优控制 MPC。以这种方式，RL 智能体在建议的最优控制器之间展示了准确性和计算时间之间的良好平衡。

可以进行进一步的分析以研究 RL 和 MPC 控制器之间的性能差异。应该指出的是，比较中没有使用先前在 [13] 中使用的相同参数。或者，对 R 和 Q（分别为控制输入和状态的权重矩阵）进行参数研究。之后，选择 R 和 Q 矩阵的最佳组合，使其实现三个间隙的最小累积 RMSE。研究结果见图 4。

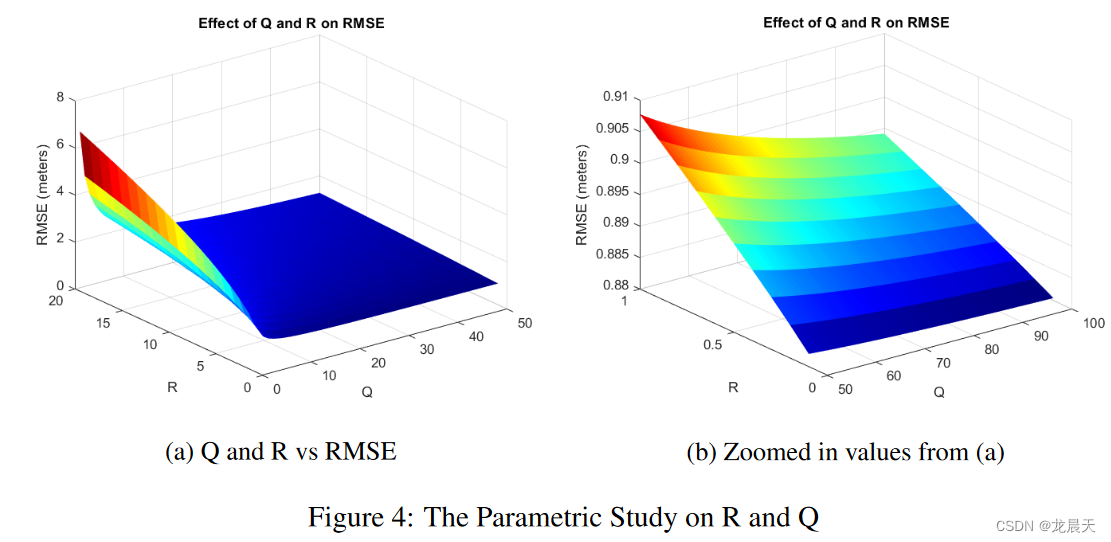
图 5b 还展示了可变间隙场景中 MPC 的间隙、速度和控制力。考虑到图 3 中 RL 智能体的响应，可以得出结论，两个控制器都以令人满意的方式满足给定的间隙和速度曲线，几乎没有显着差异。另一方面，RL 智能体通过实现更平滑的轨迹来保持其在控制工作中的主导地位。

结论

本研究解决了管理一队列异构车辆中的车辆间距的问题，其中在现有的详细非线性纵向动力学模型上开发了一个更成熟的模型，可以分别减少每辆车的空气阻力。 RL 被用作为领导者和跟随者车辆设计控制器的工具。提出了一种具有多目标奖励函数的间隙和速度控制器。该智能体基于 DDPG 算法与参与者和评论家网络进行训练。从仿真获得的结果来看，强化学习智能体在奖励函数、控制力度和速度轨迹跟踪方面表现令人满意。优化控制器的分析证实，RL 控制器在计算时间和控制工作量方面优于 MPC，特别是在更现实和复杂的场景中，同时在车辆间距中保持相似的 RMSE。

此外，建议继续在调整参数上训练模型，以获得关于可调整奖励函数的最佳性能。此外，可以延续 RL 控制器训练以满足其他目标，而不会与当前目标相抵触。硬件在环模拟器可以在广泛而逼真的模拟中使用控制器，以研究车辆在其他场景和环境下的行为。