题目描述

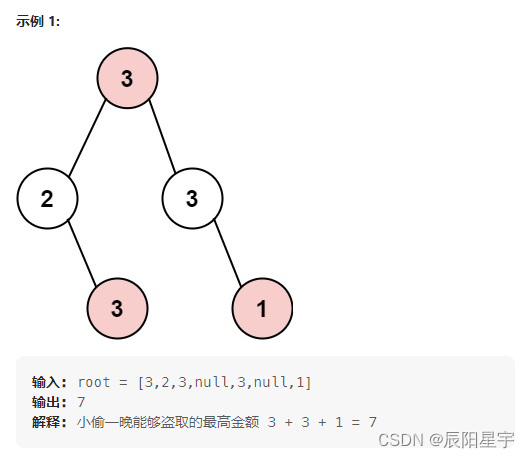
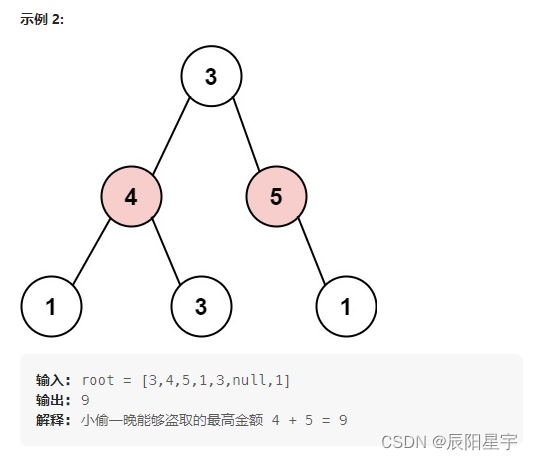
在这里插入图片描述

原题链接：337. 打家劫舍 III

解题思路

（1）记忆化递归

采用后序遍历的方式，设置一个unordered_map型Hash表record，记录每个结点的情况。当遍历到该节点时，判定之前是否遍历过，如果遍历过，直接返回record中记录结果，如果没有遍历过继续探查。因为，要找的只有两种情况，一个是不偷该节点，则向下一个结点去探查；另一个是偷该节点，则不偷下一个结点，向下下个结点去探查。最终，找到二者之间的最大值，返回。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<TreeNode*, int> record;
    int rob(TreeNode* root) {
        if(!root)                               return 0;
        if(!root->left && !root->right)         return root->val;
        // 如果当前位置已被记录过，则直接返回结果
        if(record[root] != 0)                   return record[root];
        // val1：不偷当前结点，val2：偷当前结点
        int val1 = 0, val2 = root->val;
        val1 = rob(root->left) + rob(root->right);
        if(root->left)          val2 += rob(root->left->left) + rob(root->left->right);
        if(root->right)         val2 += rob(root->right->left) + rob(root->right->right);
        record[root] = max(val1, val2);

        return max(val1, val2);
    }
};

（2）动态规划

递归三步曲 + 动态规划五步曲

（1）确定递归函数参数和返回值：

vector<int> robTree(TreeNode* root)

参数为root，返回值为长度为2的dp数组，下标0表示不偷root的结果，下标1表示偷root的结果。

（2）确定终止条件：

if(!root)           return vector<int>{0, 0};

当遍历到空节点时，返回{0, 0}

（3）确定遍历顺序：

因为dp数组是从小到大，大的要基于小的结果去进行操作。所以，需要使用后序遍历的方式，左右中的顺序遍历。底层的结果返回给上一层，上一层处理完后再返回给其上一层。

（4）确定单层递归逻辑：
对左右遍历完后，用val1记录不偷时的情况，找出偷下一个结点值更大，还是不偷下一个结点值更大。用val2记录偷时的情况，当前结点加上不偷下一个结点时的情况。

（5）举例：

/**
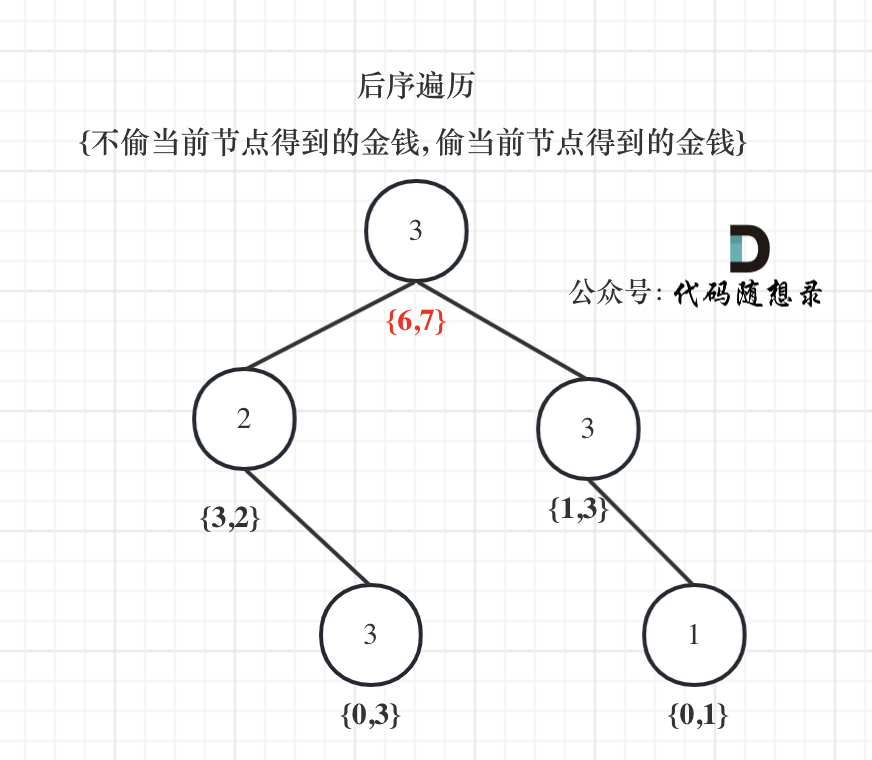
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:    
    // 每次返回一个长度为2的数组，下标0：不偷的结果，下标1：偷的结果，取二者中的最大值
    vector<int> robTree(TreeNode* root) {
        if(!root)           return vector<int>{0, 0};
        vector<int> left = robTree(root->left);
        vector<int> right = robTree(root->right);
        // val1：不偷，val2：偷        
        int val1 = max(left[0], left[1]) + max(right[0], right[1]);
        int val2 = root->val + left[0] + right[0];
        
        return {val1, val2};
    }
    int rob(TreeNode* root) {
        vector<int> res = robTree(root);
        return max(res[0], res[1]);
    }
};