打卡第二天，认真做了两道题目，顶不住了好困，明天早上练完车回来再重新看看。

今日任务

第一章数组

• 977.有序数组的平方
• 209.长度最小的子数组
• 59.螺旋矩阵II

977.有序数组的平方

示例 1:
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2:
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

我的解题

暴力做法

void quick_sort(vector<int> &q, int l, int r) {
    if(l >= r) return;
    int i = l - 1, j = r + 1, x = q[(l + r) >> 1];
    while(i < j) {
        do i++; while(q[i] < x);
        do j--; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}
vector<int> sortedSquares(vector<int>& nums) {
    for(int i = 0; i < nums.size(); i++) nums[i] *= nums[i];
    quick_sort(nums, 0, nums.size() - 1);
    // sort(nums.begin(), nums.end());
    return nums;
}

看完题目第一想法，暴力把数组每一个数的平方先的出来，然后快排。

双指针做法

vector<int> sortedSquares(vector<int>& nums) {
    vector<int> res(nums.size(), 0);
    int z = 0;
    while(z < nums.size() && nums[z] < 0) ++z;
    int k = 0, i = z - 1, j = z;
    while(i >= 0 && j < nums.size()) {
        if(nums[i] * nums[i] <= nums[j] * nums[j]) {
            res[k++] = nums[i] * nums[i];
            i--;
        } else {
            res[k++] = nums[j] * nums[j];
            j++;
        }
    }
    while(i >= 0) {
            res[k++] = nums[i] * nums[i];
            i--;
    }
    while(j < nums.size()){
            res[k++] = nums[j] * nums[j];
            j++;
    }
    return res;
}

双指针想法，因为是非递减数组，有正数负数，平方之后中间的数小，两边的大。

• 新建一个数组res，存放结果。
• 找到第一个正数下标z，因为是非递减数组，所以从这个数开始分成两边，平方之后左边 <- 越来越大，右边 -> 越来越大，
• 比较 $nums[i](i=z-1)，nums[j](j-z)$下标的值的平方哪个更小，小的存入结果数组res，移动指针。如果 $nums[i]\ast nums[i]<nums[j]\ast nums[j]$, 将 $nums[i]\ast nums[i]$ 存入 res, i 往左边移动一格。
• 当i，j 某一个指针到了边界，将另外一个还没到边界的指针后面的值平方存到结果数组。注意 i ，j指针一个往左，一个往右。

看完卡哥的题解，发现自己把题目搞复杂了，直接在头尾两边定义指针，把大的平方数的指针指向的数的平方，存到结果数组（从后往前存放）就行，当指针相遇后结束就可以了。

代码随想录

看完卡哥的题解，

vector<int> sortedSquares(vector<int>& nums) {
    vector<int> res(nums.size(), 0);
    int i = 0, j = nums.size() - 1;
    int k = nums.size() - 1;
    for(int i = 0, j = nums.size() - 1; i <= j;) {
        if(nums[i] * nums[i] >= nums[j] * nums[j]) {
            res[k--] = nums[i] * nums[i];
            i++;
        } else {
            res[k--] = nums[j] * nums[j];
            j--;
        }
    }
    return res;
}

209.长度最小的子数组

示例1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例2：
 输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

题解

int minSubArrayLen(int target, vector<int>& nums) {
    int result = INT_MAX;
    int sum = 0; // 滑动窗口的值
    int hh = 0; // 滑动窗口的起始位置
    int length = 0; // 滑动窗口的长度
    for(int i = 0; i < nums.size(); i++) {
        sum += nums[i];
        while(sum >= target) {
            length = i - hh + 1;
            result = min(result, length);
            sum -= nums[hh++];
        }
    }
    if(result != INT_MAX) return result;
    else return 0;
}

这道题之前做过，也看过卡哥的视频，知道用滑动窗口，但是忘记怎么写了，又重新温习了一遍。

定义一个滑动窗口，把原数组的值加到窗口里面并且计算总值，当总值超过目标值，开始从窗口头缩小窗口，直到滑动数组的值不超过目标值，继续往窗口加原数组的值，直到遍历完数组。

59.螺旋矩阵II

示例1：
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

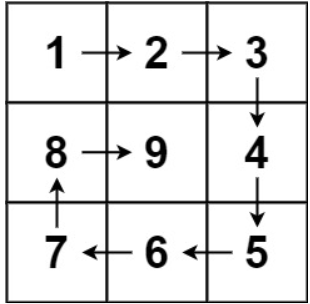
示例2：
 输入：n = 1
输出：[[1]]

题解

vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> result(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
        int startx = 0, starty = 0;
        int offset = 1; // 圈数缩小大小
        int count = 1;
        int i = 0, j = 0;
        int loop = n / 2; // 矩阵循环圈数
        int mid = n / 2;
        while(loop--) {
            i = startx;
            j = starty;
            for(j = starty; j < n - offset; j++) {
                result[startx][j] = count++;
            }
            for(i = startx; i < n - offset; i++) {
                result[i][j] = count++;
            }
            for(;j > starty; j--) {
                result[i][j] = count++;
            }
            for(; i > startx; i--) {
                result[i][starty] = count++;
            }
            startx++;
            starty++;
            offset++;
        }
        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2) {
            result[mid][mid] = count;
        }
        return result;
    }