[Datawhale][CS224W]图机器学习(三)

news2024/11/14 20:57:37

目录

    • 一、简介与准备
    • 二、教程
      • 2.1 下载安装
      • 2.2 创建图
        • 2.2.1 常用图创建（自定义图创建）
          • 1.创建图对象
          • 2.添加图节点
          • 3.创建连接
        • 2.2.2 经典图结构
          • 1.全连接无向图
          • 2.全连接有向图
          • 3.环状图
          • 4.梯状图
          • 5.线性串珠图
          • 6.星状图
          • 7.轮辐图
          • 8.二项树
        • 2.2.3 栅格图
          • 1.二维矩形栅格图
          • 2.多维矩形栅格图
          • 3.二维三角形栅格图
          • 3.二维六边形栅格图
          • 4.n维超立方体图
        • 2.2.4 NetworkX内置图
          • 1.钻石图
          • 2.牛角图
          • 3.荔枝图？（虽然看不出跟荔枝有啥联系）
          • 4.房子图
          • 5.房子x图
          • 6.风筝图
        • 2.2.5 随机图
        • 2.2.6 无标量有向图
        • 2.2.7 社交网络
          • 1.空手道俱乐部数据集
          • 2.雨果《悲惨世界》任务关系
          • 3.家庭关系图
        • 2.2.8 社群聚类图
        • 2.2.9 树结构
      • 2.3 常用信息获取
      • 2.4 图可视化
        • 2.4.1 初始化
        • 2.4.2 原生可视化
        • 2.4.3 不显示节点
        • 2.4.4 设置颜色
        • 2.4.5 无向图转有向图后显示
        • 2.4.6 通过设置每个节点的坐标来显示图
        • 2.4.7 绘制房子图（例子）
        • 2.4.8 可视化模板（重要）
        • 2.4.9 自我中心图(ego图)
      • 2.5 图相关数据分析
        • 2.5.1 计算PageRank节点重要度
        • 2.5.2 最大连通域子图
        • 2.5.3 每个节点的连接数（degree）
        • 2.5.4 一些可能用到的图的基础数据
        • 2.5.5 节点特征（重要）
        • 2.5.6 计算全图的Graphlet
  • 参考文献

Datawhale开源学习社区 x 同济子豪兄 Stanford课程中文精讲系列笔记
本文同时发布在：本人博客https://wumorfr.github.io/

一、简介与准备

NetworkX用于实现创建，操作和研究复杂网络的结构，动态功能

几个常用链接

  • NetworkX 主页
  • NetworkX 文档
  • NetworkX 文档 PDF

本文接下来使用环境包括

import networkx
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib as mpl
import pandas as pd
import matplotlib.colors as mcolors

# %matplotlib inline #anconda中使用时要添加

# windows系统
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示正负号

二、教程

2.1 下载安装

本人是使用pip安装（使用了清华源）

pip install networkx -i https://pypi.tuna.tsinghua.edu.cn/simple

安装好后可在python环境下运行

import networkx as nx

print("nx.__version__: " + nx.__version__)

进行校验输出，结果类似如下

请添加图片描述

2.2 创建图

本列表中2.2.2至2.2.9暂时视为不常用，因为本人初学使用时基本很少看到，了解即可，可视作资料库，用的时候再查。不过2.2.7中数据集有的时候会用可以多看两眼（笑）

2.2.1 常用图创建（自定义图创建）

1.创建图对象
G = nx.Graph()          # 空无向图 （重要）
G = nx.DiGraph()        # 空有向图 （重要）
G = nx.MultiGraph()     # 空多重无向图 
G = nx.MultiDigraph()   # 空多重有向图 
G.clear()               # 清空图
2.添加图节点

此处先创建一个无节点无连接的空图G和另一个首尾相连成串的Path Graph H

G =nx.Graph()
H =nx.path_graph(10)

G.add_node('刘备')  					   # 添加单个节点
G.add_nodes_from(['诸葛亮','曹操'])		 # 三、添加多个节点
G.add_nodes_from([
    ('关羽',{'武器':'青龙偃月刀','武力值':90,'智力值':80}),
    ('张飞',{'武器':'八丈蛇矛','武力值':85,'智力值':75}),
    ('吕布',{'武器':'方天画戟','武力值':100,'智力值':70})
])										# 添加带属性的节点


G.add_nodes_from(H)						# 将H的节点添加到G中
print("G.nodes",G.nodes)
print("G.len",len(G))

G.add_node(H)							# 将H本身作为一个节点添加进G中
print("G.nodes",G.nodes)
print("G.len",len(G))

结果：

image-20230215163958329

注意：

add_node和add_nodes_from
对于add_node加一个点来说，字符串是只添加了名字为整个字符串的节点。但是对于add_nodes_from加一组点来说，字符串表示了添加了每一个字符都代表的多个节点，exp：

g.add_node("spam") #添加了一个名为spam的节点
g.add_nodes_from("spam") #添加了4个节点，名为s,p,a,m

小结
节点可以为任意可哈希的对象，比如字符串、图像、XML对象，甚至另一个Graph、自定义的节点对象
通过这种方式可以根据自己的使用灵活的自由构建：以图、文件、函数为节点等灵活的图的形式

3.创建连接

此处先创建无向空图G和有向空图H

# 创建无向空图

G = nx.Graph()
print(G.is_directed())
# 给整张图添加属性特征
G.graph['Name'] = "HelloWord"
print(G.graph)
# 创建有向空图
H = nx.DiGraph()
print(H.is_directed())

输出：

请添加图片描述
image-20230215164244721

G.add_node(0,feature=5,label=0,zihao=2)		# 创建单个节点，此处为创建0号节点，并添加特征属性
G.add_nodes_from([
    (1,{'feature':1,'label':1,'zihao':3}),
    (2,{'feature':2,'label':2,'zihao':4})
])											# 创建多个节点

全图节点信息：

print(G.number_of_nodes())
print(G.nodes)
print(G.nodes(data=True))

# 遍历所有节点，data=True表示输出节点特征属性信息
for node in G.nodes(data=True):
    print(node)

image-20230215164450313

此时点均为散点，后创立连接

G.add_edge(0,1,weight=0.5,like=3)	# 创建单个连接，设置属性特征
G.add_edges_from([
    (1,2,{'weight':0.3,'like':5}),
    (2,0,{'weight':0.1,'like':8})
])									# 创建多个连接

连接情况

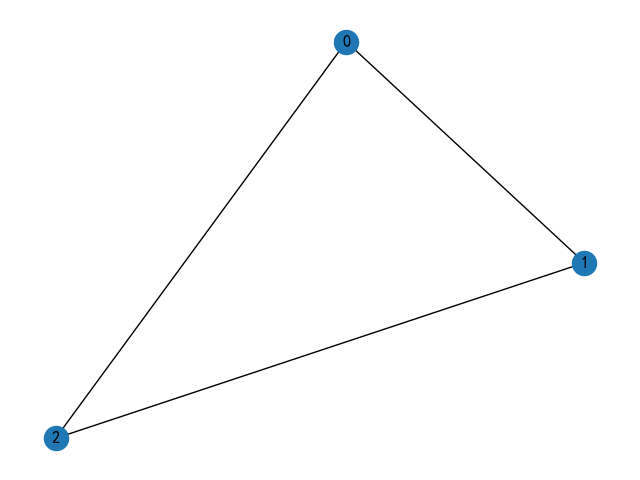
image-20230215164802782

全图连接信息

print(G.number_of_nodes())
print(G.size())
print(G.edges())
print(G.edges(data=True))

# 遍历所有连接，data=True表示输出连接特征属性信息
for edge in G.edges(data=True):
    print(edge)

image-20230215164857264

查询节点的连接数

  • 指定节点
node_id=1
print(G.degree[node_id])
  • 指定节点的所有相邻节点
for neighbor in G.neighbors(node_id):
    print("Node {} has neighbor {}".format(node_id,neighbor))

image-20230215165055688

  • 所有节点
for node_id in G.nodes():
    for neighbor in G.neighbors(node_id):
        print("Node {} has neighbor {}".format(node_id,neighbor))

image-20230215165109487

2.2.2 经典图结构

1.全连接无向图
G = nx.complete_graph(7)
nx.draw(G)
plt.show()
# 全图连接数
print("全图连接数:", G.size())
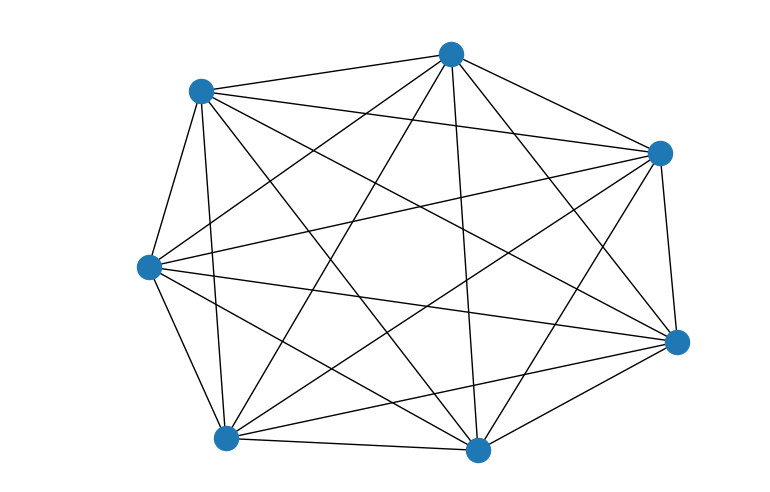
image-20230215152516233
2.全连接有向图
G = nx.complete_graph(7, nx.DiGraph())
nx.draw(G)
plt.show()

# 是否是有向图
print("是否是有向图:", G.is_directed())
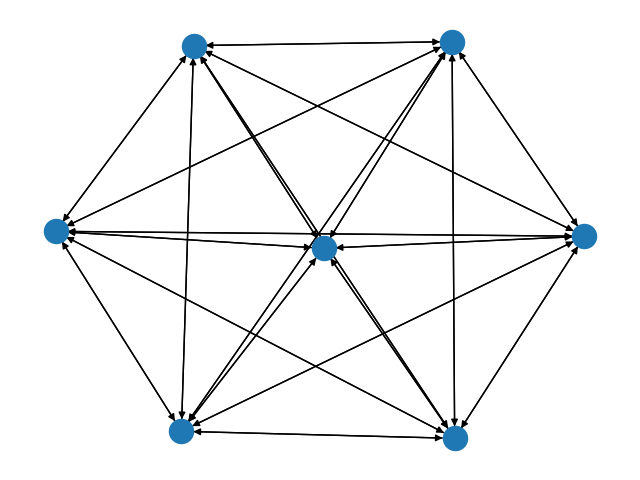
image-20230215152629209
3.环状图
G = nx.cycle_graph(5)
nx.draw(G)
plt.show()
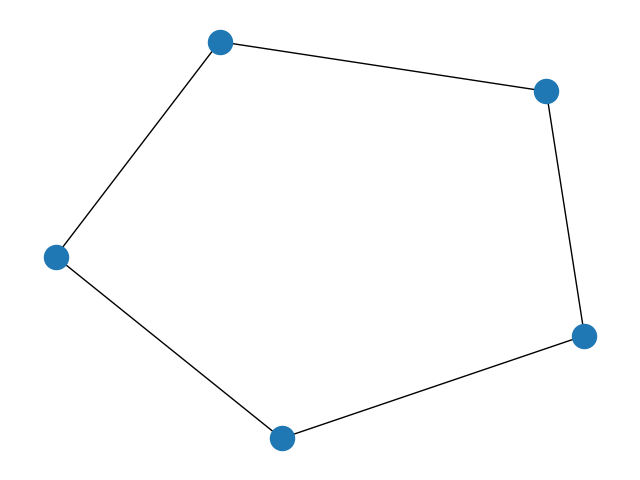
image-20230215152737274
4.梯状图
G = nx.ladder_graph(5)
nx.draw(G)
plt.show()
image-20230215153016675
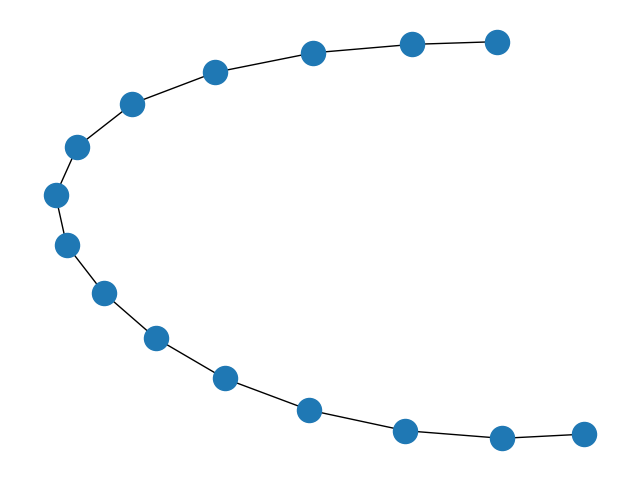
5.线性串珠图
G = nx.path_graph(15)
nx.draw(G)
plt.show()
image-20230215153022746
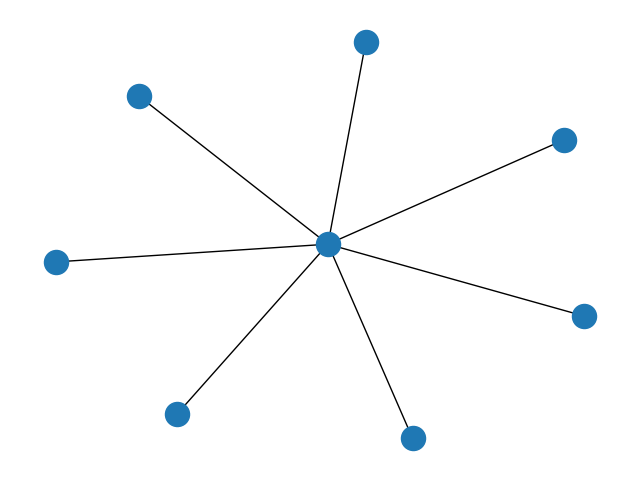
6.星状图
G = nx.star_graph(7)
nx.draw(G)
plt.show()
image-20230215153145635
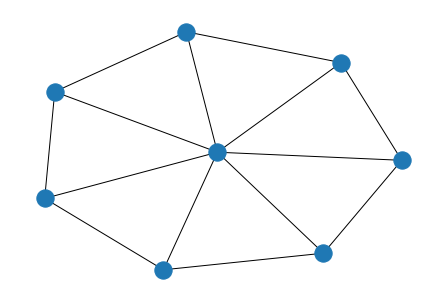
7.轮辐图
G = nx.wheel_graph(8)
nx.draw(G)
plt.show()
image-20230215160313034
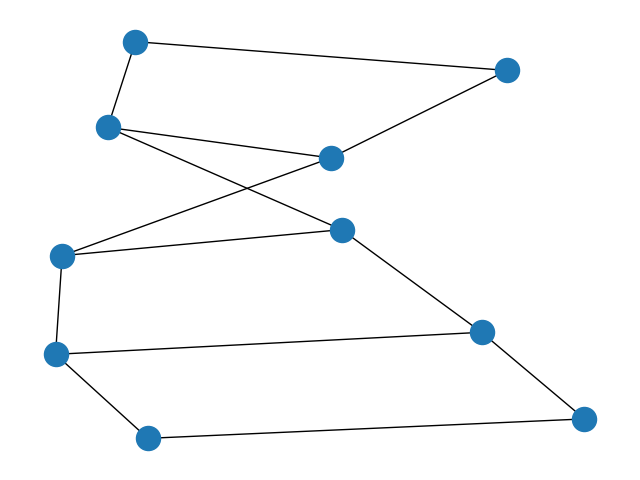
8.二项树
G = nx.binomial_tree(5)
nx.draw(G)
plt.show()
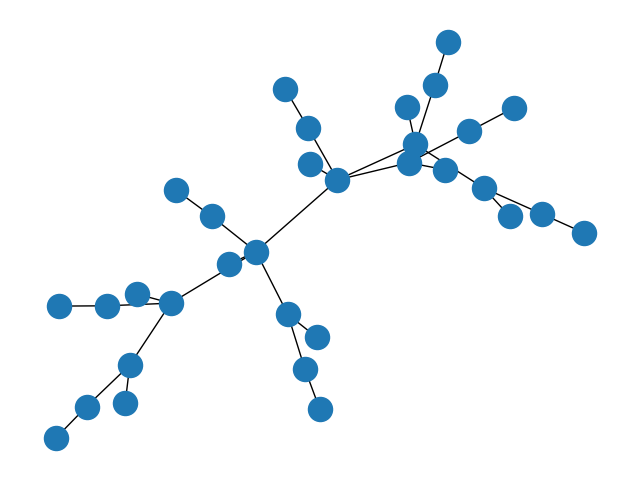
image-20230215160429336

2.2.3 栅格图

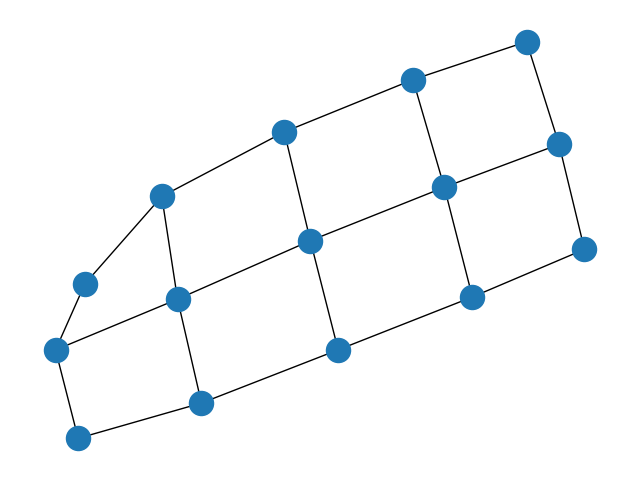
1.二维矩形栅格图
G = nx.grid_2d_graph(3, 5)
nx.draw(G)
plt.show()
image-20230215160351008
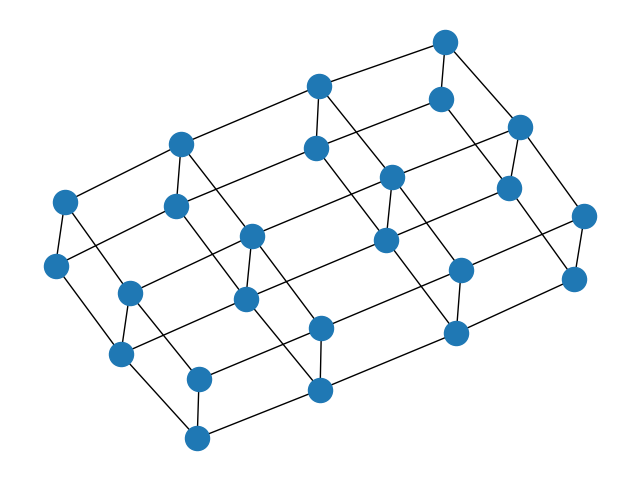
2.多维矩形栅格图
G = nx.grid_graph(dim=(2, 3, 4))
nx.draw(G)
plt.show()
image-20230215160508449
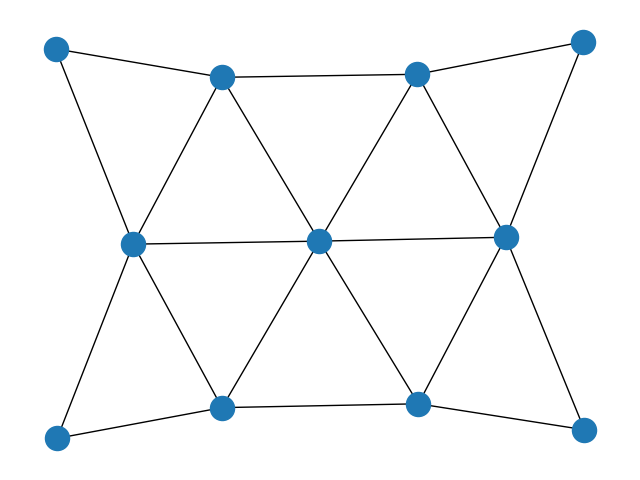
3.二维三角形栅格图
G = nx.triangular_lattice_graph(2, 5)
nx.draw(G)
plt.show()
image-20230215161233443
3.二维六边形栅格图
G = nx.hexagonal_lattice_graph(2, 3)
nx.draw(G)
plt.show()
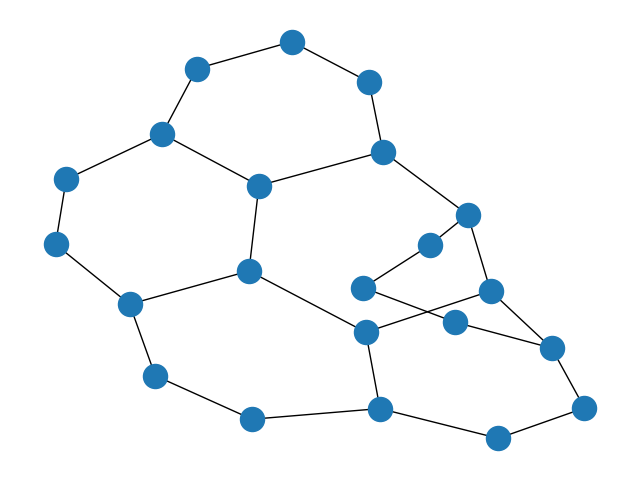
image-20230215161255890
4.n维超立方体图
G = nx.hypercube_graph(4)
nx.draw(G)
plt.show()
image-20230215161303145

2.2.4 NetworkX内置图

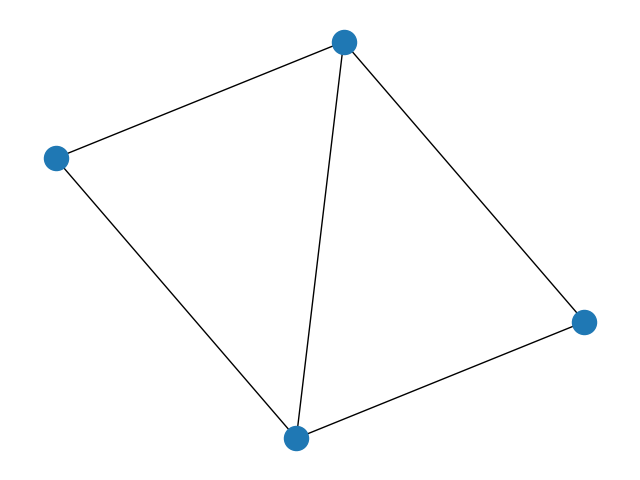
1.钻石图
G = nx.diamond_graph()
nx.draw(G)
plt.show()
image-20230215161308922
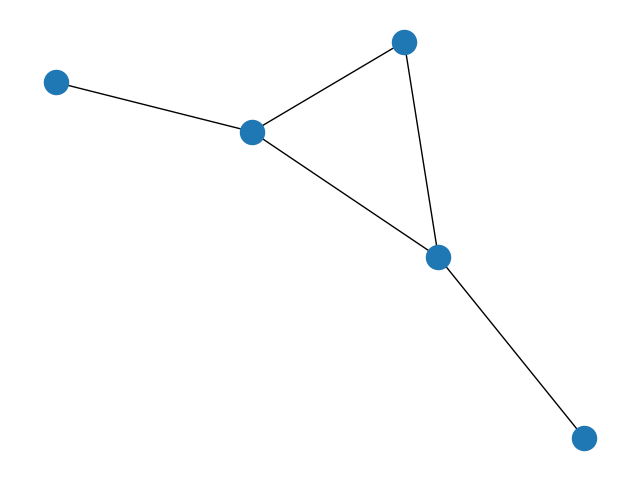
2.牛角图
G = nx.bull_graph()
nx.draw(G)
plt.show()
image-20230215161314465
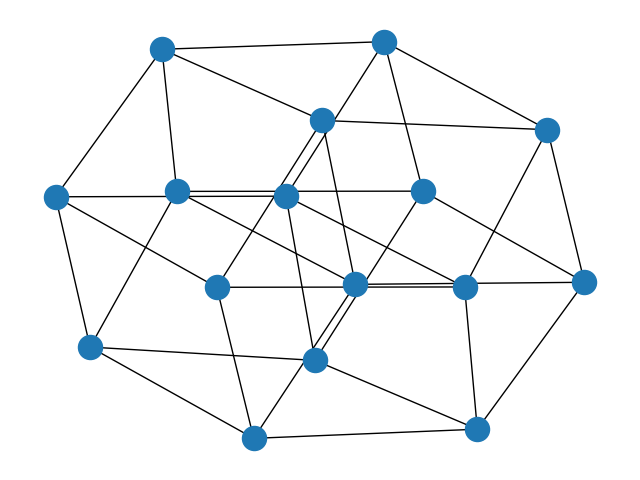
3.荔枝图？（虽然看不出跟荔枝有啥联系）
G = nx.frucht_graph()
nx.draw(G)
plt.show()
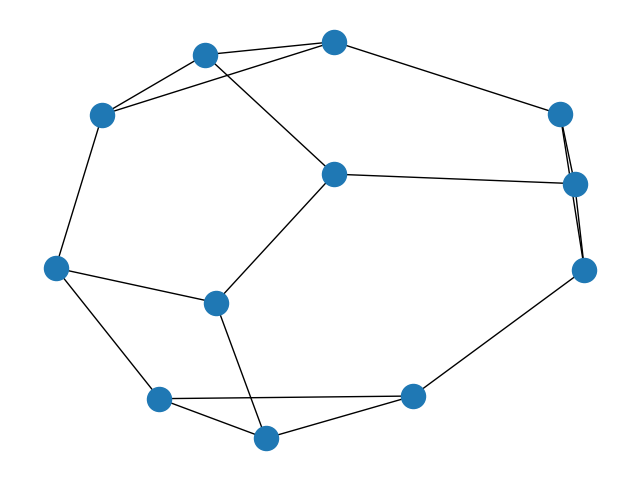
image-20230215161319011
4.房子图
G = nx.house_graph()
nx.draw(G)
plt.show()
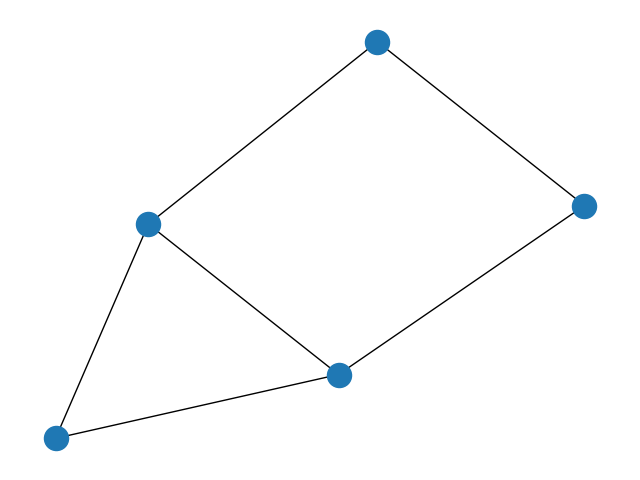
image-20230215161324489
5.房子x图
G = nx.house_x_graph()
nx.draw(G)
plt.show()
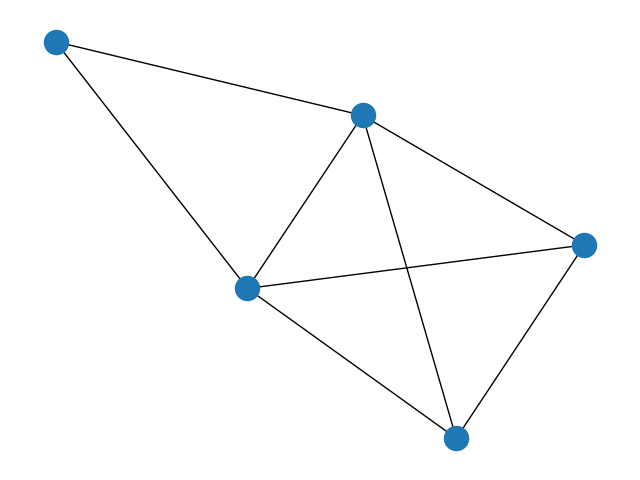
image-20230215161331817
6.风筝图
G = nx.krackhardt_kite_graph()
nx.draw(G)
plt.show()
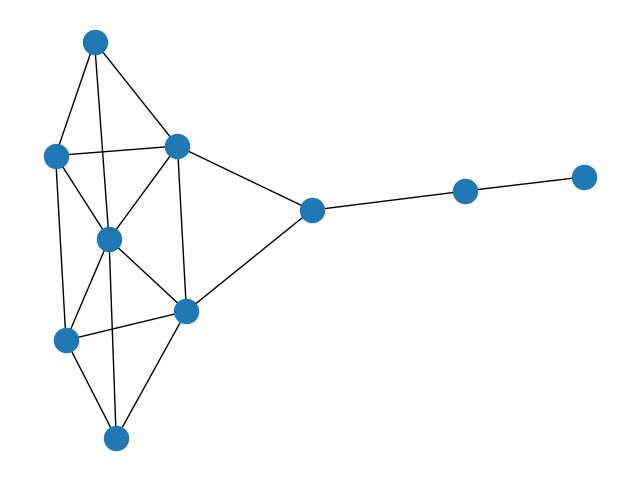
image-20230215161337898

2.2.5 随机图

G = nx.erdos_renyi_graph(10, 0.5)
nx.draw(G)
plt.show()
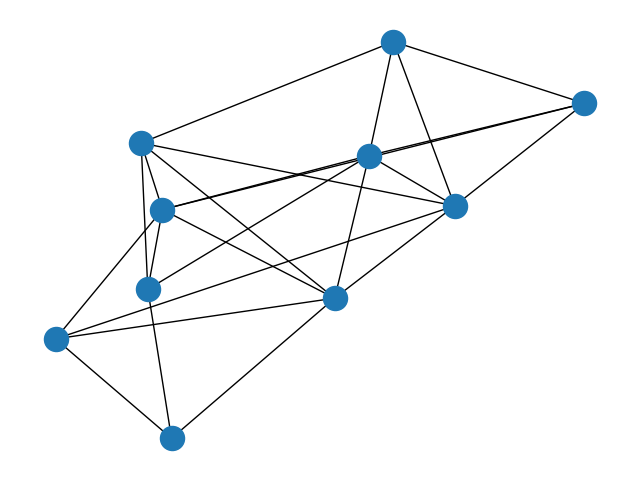
image-20230215161343699

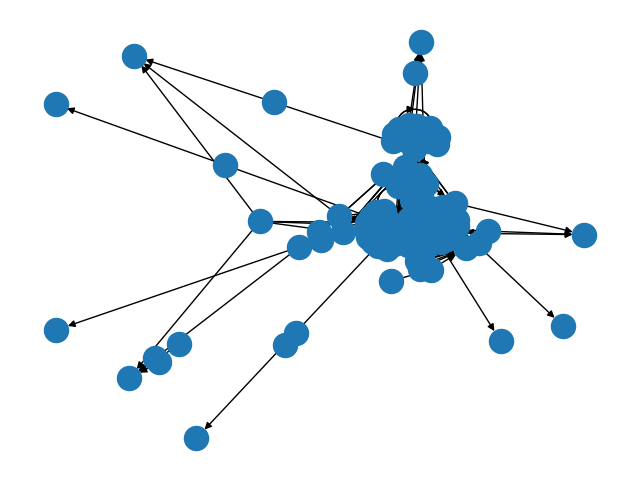
2.2.6 无标量有向图

G = nx.scale_free_graph(100)
nx.draw(G)
plt.show()
image-20230215161510350

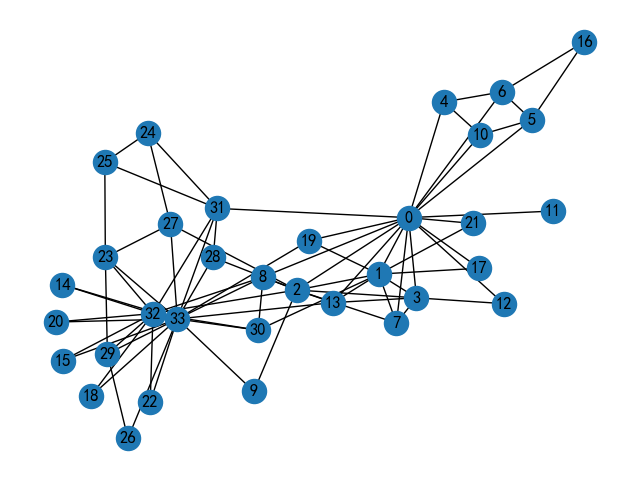
2.2.7 社交网络

1.空手道俱乐部数据集
G = nx.karate_club_graph()
nx.draw(G, with_labels=True)
plt.show()
print(G.nodes[5]["club"])
print(G.nodes[9]["club"])
image-20230215161738105
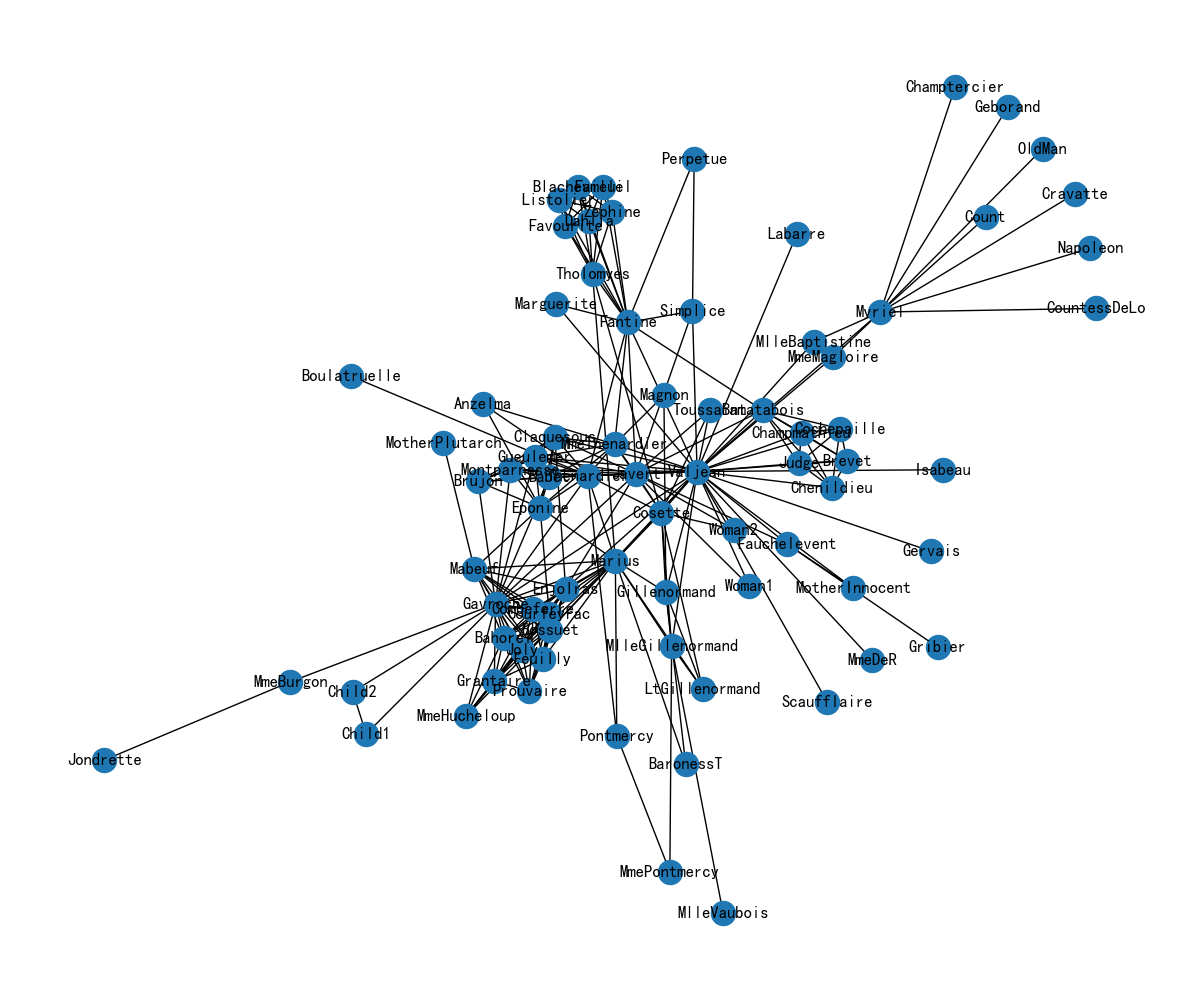
2.雨果《悲惨世界》任务关系
G = networkx.les_miserables_graph()
plt.figure(figsize=(12, 10))
pos = nx.spring_layout(G, seed=10)
nx.draw(G, pos, with_labels=True)
plt.show()
plt.show()
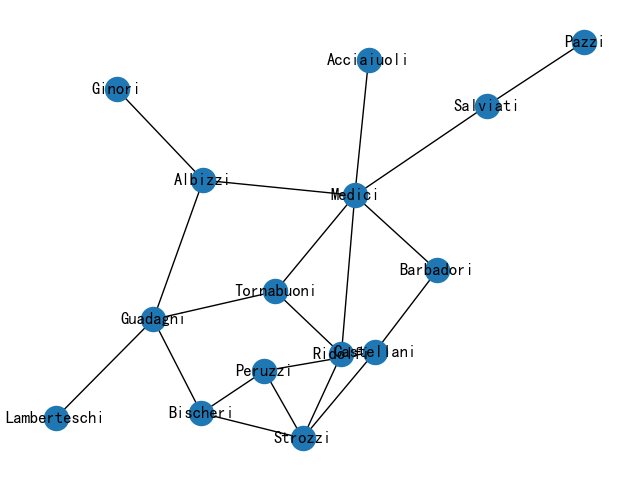
image-20230215161745061
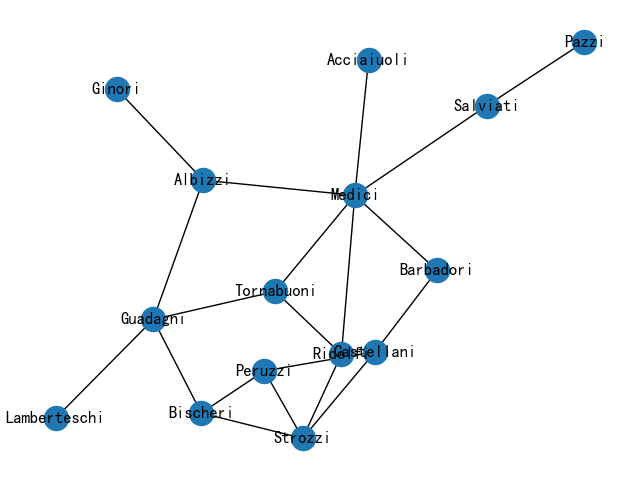
3.家庭关系图
G = nx.florentine_families_graph()
nx.draw(G, with_labels=True)
plt.show()
image-20230215161821925

2.2.8 社群聚类图

G = nx.caveman_graph(4, 3)
nx.draw(G, with_labels=True)
plt.show()
image-20230215161817189

2.2.9 树结构

tree = nx.random_tree(n=10, seed=0)
print(nx.forest_str(tree, sources=[0]))

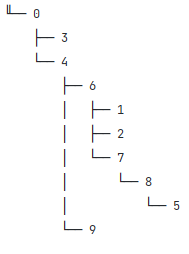
image-20230215161933569

2.3 常用信息获取

nx.info(G) # 图信息的概览
G.number_of_nodes()
G.number_of_edges()

# 获取和节点idx连接的边的attr属性之和
G.in_degree(idx, weight='attr')

# 如果想知道某个结点相连的某个边权之和：
DG.degree(nodeIdx, weight='weightName')

# 获取结点或者边的属性集合，返回的是元组的列表
G.nodes.data('attrName')
G.edges.data('attrName')

# 获取n1 n2的边的length权重，那么:
G[n1][n2]['length']

# 如果是有重边的图，选择n1,n2第一条边的length权重，则:
G[n1][n2][0]['length']

# 获取n1结点的所有邻居
nx.all_neighbors(G, n1)

# 判断图中n1到n2是否存在路径
nx.has_path(G, n1, n2)

# 根据一个结点的list，获取子图
subG = nx.subgraph(G, nodeList)

2.4 图可视化

2.4.1 初始化

创建4*4网格图（无向图）
G = nx.grid_2d_graph(4,4)

2.4.2 原生可视化

pos = nx.spring_layout(G,seed=123)
nx.draw(G,pos)
plt.show()

2.4.3 不显示节点

nx.draw(G,pos,node_size=0,with_labels=False)
plt.show()

2.4.4 设置颜色

print(len(G.edges()))
nx.draw(
    G,
    pos,
    node_color = '#66ccff',  # 节点颜色
    edgecolors='red',       # 节点外边缘颜色
    edge_color='blue',      # edge的颜色

    # edge_cmap=plt.cm.coolwarm,# 配色方案

    node_size=800,
    with_labels=False,
    width=3,
)
plt.show()

2.4.5 无向图转有向图后显示

nx.draw(
    G.to_directed(),		# 关键是这一句
    pos,
    node_color = '#66ccff',  # 节点颜色
    edgecolors='red',       # 节点外边缘颜色
    edge_color='tab:gray',  # edge的颜色

    # edge_cmap=plt.cm.coolwarm,# 配色方案

    node_size=800,
    with_labels=False,
    width=3,
    arrowsize=10,
)
plt.show()

2.4.6 通过设置每个节点的坐标来显示图

# 无向图
# 初始化图
G = nx.Graph()
G.add_edge(1,2)
G.add_edge(1,3)
G.add_edge(1,5)
G.add_edge(2,3)
G.add_edge(3,4)
G.add_edge(4,5)
nx.draw(G,with_labels=True)
plt.show()

# 关键代码
# 设置每个节点可视化的坐标
pos={1:(0,0),2:(-1,0.3),3:(2,0.17),4:(4,0.255),5:(5,0.03)}

# 设置其他可视化格式
options = {
    "font_size":36,
    "node_size":3000,
    "node_color":"white",
    "edgecolors":"black",
    "linewidths":5, # 节点线宽
    "width": 5,     # edge线宽
}

nx.draw_networkx(G,pos,**options)

ax=plt.gca()
ax.margins(0.20)    # 在图的边缘留白，防止节点被截断
plt.axis("off")
plt.show()


# 有向图
G = nx.DiGraph([(0,3),(1,3),(2,4),(3,5),(3,6),(4,6),(5,6)])
nx.draw(G,with_labels=True)
plt.show()


# 可视化每一列包含的节点
left_nodes=[0,1,2]
middle_nodes=[3,4]
right_nodes=[5,6]

# 可视化时每个节点的坐标
pos = {n:(0,i) for i ,n in enumerate(left_nodes)}
pos.update({n:(1,i+0.5)for i,n in enumerate(middle_nodes)})
pos.update({n:(2,i+0.5)for i,n in enumerate(right_nodes)})

print(pos)


nx.draw_networkx(G,pos,**options)

ax=plt.gca()
ax.margins(0.20)    # 在图的边缘留白，防止节点被截断
plt.axis("off")
plt.show()

2.4.7 绘制房子图（例子）

# 尝试绘制房子图
G = nx.Graph([(0,1),(0,2),(1,3),(2,3),(2,4),(3,4)])

pos = {0:(0,0),1:(1,0),2:(0,1),3:(1,1),4:(0.5,2.0)}

plt.figure(figsize=(10,8))
nx.draw_networkx_nodes(G,pos,node_size=3000,nodelist=[0,1,2,3],node_color="#66ccff")
nx.draw_networkx_nodes(G,pos,node_size=3000,nodelist=[4],node_color="tab:orange")
nx.draw_networkx_edges(G,pos,alpha=0.5,width=6)
plt.axis("off")     # 关闭坐标轴
plt.show()

2.4.8 可视化模板（重要）

# 一、基础可视化
# 创建有向图
seed=114514
G=nx.random_k_out_graph(10,3,0.5,seed=seed)
pos=nx.spring_layout(G,seed=seed)

# 初步可视化
nx.draw(G,pos=pos,with_labels=True)
plt.show()

# 二、高级可视化
# 节点大小
node_sizes = [12+10*i for i in range(len(G))]
print(node_sizes)

# 节点颜色
M = G.number_of_edges()
edge_colors = range(2,M+2)
print(edge_colors)

# 节点透明度
edge_alphas = [(5+i)/(M+4)for i in range(M)]
print(edge_alphas)

# 配色方案
cmap = plt.get_cmap('plasma')
# cmap = plt.cm.Blues

plt.figure(figsize=(10,8))

# 绘制节点
nodes = nx.draw_networkx_nodes(G,pos,node_size=node_sizes,node_color="indigo")

# 绘制链接

edges = nx.draw_networkx_edges(
    G,
    pos,
    node_size=node_sizes,    # 节点尺寸
    arrowstyle="->",        # 箭头样式
    arrowsize=20,           # 箭头尺寸
    edge_color=edge_colors,  # 连接颜色
    edge_cmap=cmap,         # 连接配色方案
    width=4                 # 连接线宽
)

# 设置每个连接的透明度
for i in range(M):
    edges[i].set_alpha(edge_alphas[i])

# 调色图例
pc = mpl.collections.PathCollection(edges,cmap=cmap)
pc.set_array(edge_colors)
plt.colorbar(pc)

ax=plt.gca()
ax.set_axis_off()
plt.show()

2.4.9 自我中心图(ego图)

Ego graph指距离中心节点小于特定距离（特定路径长度）的所有结点构成的图，特定距离通常为1，即与中心节点直接有边连接。例如，假设下图左为一个完整的图，图右为以 D D D为中心节点的ego-graph。换句话说，所谓的ego network，它的节点是由唯一的一个中心节点(ego)，以及这个节点的邻居(alters)组成的，它的边只包括了ego和alter之间，以及alter与alter之间的边。

有的也称为Ego Network。

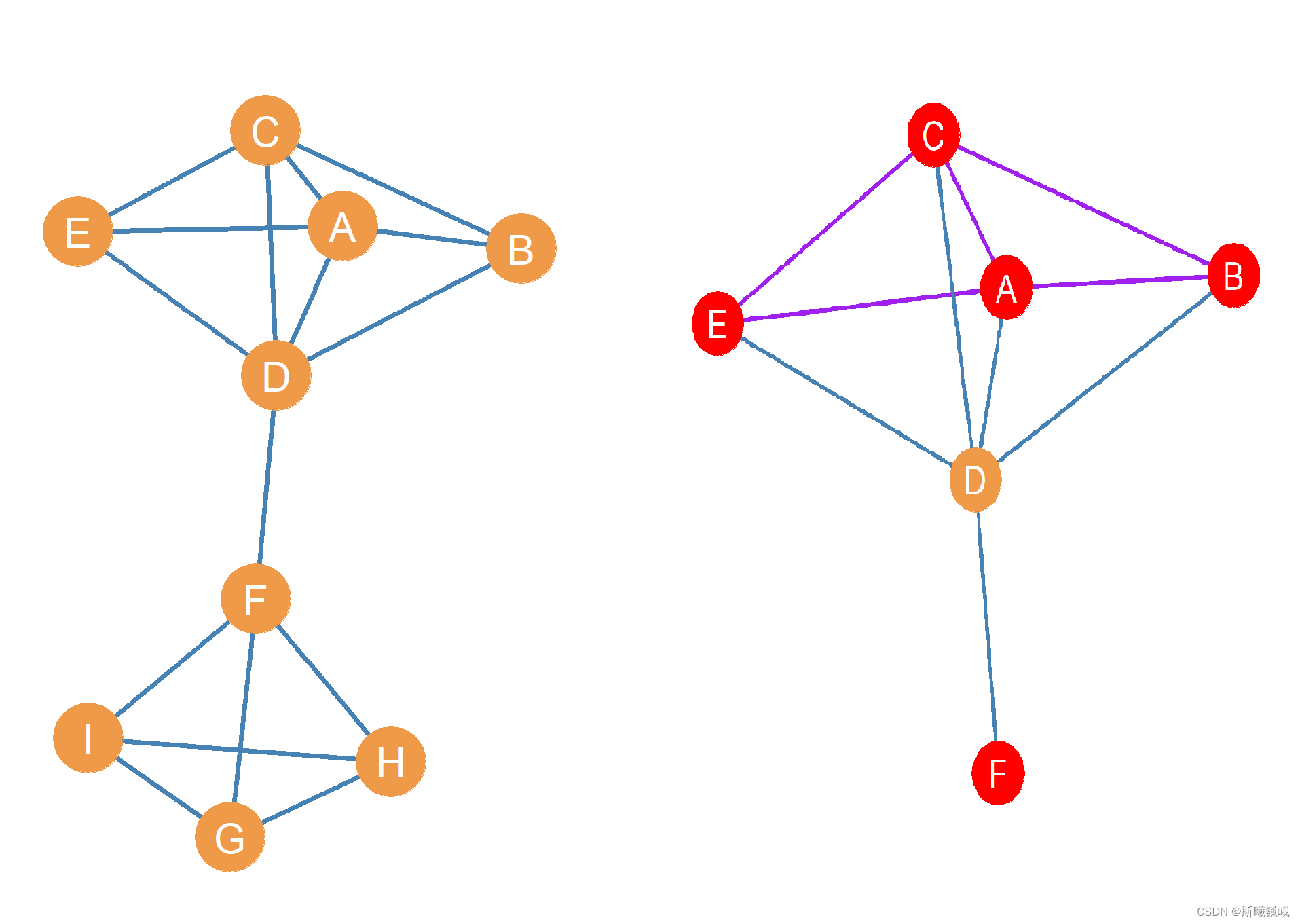
ego-graph

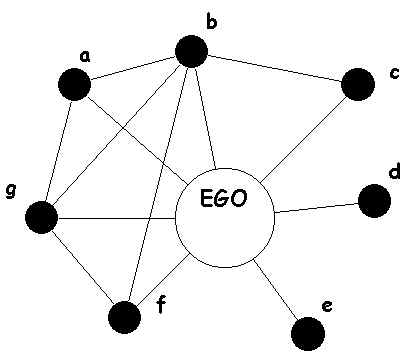
egonet3

其中，图里面的每个alter和它自身的邻居又可以构成一个ego network，而所有节点的ego network合并起来，就可以组成真实的social network了。

Ego graph中的中心被称为ego（ D D D），而其它与ego连接的节点被称为alter（ A , B , C , E , F A,B,C,E,F A,B,C,E,F）。

在ego图中，除了ego与alter之间有边外，例如 { D A , D B , D C , D E , D F } \{DA, DB,DC,DE,DF\} {DA,DB,DC,DE,DF}，alter和alter之间也可以存在边（可选的，可能存在也可能不存在），例如 { A C , A B , A E , B C , C E } \{AC,AB,AE,BC,CE\} {AC,AB,AE,BC,CE}。

跟ego graph有关联的有一个称之为N-step neighborhood的概念，它指的是与同ego间路径长度为 N N N的所有“邻居”。

2.5 图相关数据分析

2.5.1 计算PageRank节点重要度

G =nx.star_graph(7)
nx.draw(G,with_labels=True)

# 计算PageRank节点重要度

PageRank = nx.pagerank(G,alpha=0.8)
print(PageRank)

2.5.2 最大连通域子图

# 一、创建图
# 创建 Erdos-Renyi 随机图，也称作 binomial graph
# n-节点数
# p-任意两个节点产生连接的概率

G = nx.gnp_random_graph(100,0.02,seed=10374196)

# 初步可视化
pos = nx.spring_layout(G,seed=10)
nx.draw(G,pos)
plt.show()
# 二、最大连通阈子图
Gcc = G.subgraph(sorted(nx.connected_components(G),key=len,reverse=True)[0])

pos=nx.spring_layout(Gcc,seed=1039653)

nx.draw_networkx_nodes(Gcc,pos,node_size=20)
nx.draw_networkx_edges(Gcc,pos,alpha=0.4)
plt.show()

2.5.3 每个节点的连接数（degree）

G = nx.gnp_random_graph(100,0.02,seed=10374196)

# 排序一下
degree_sequence = sorted((d for n, d in G.degree()), reverse=True)
print(degree_sequence)

2.5.4 一些可能用到的图的基础数据

 导入图
# 第一个参数指定头部节点数，第二个参数指定尾部节点数
G = nx.lollipop_graph(4, 7)

# 可视化
pos = nx.spring_layout(G, seed=3068)
nx.draw(G, pos=pos, with_labels=True)
plt.show()

# 图数据分析
# 半径
print(nx.radius(G))
# 直径
print(nx.diameter(G))
# 偏心度：每个节点到图中其它节点的最远距离
print(nx.eccentricity(G))
# 中心节点，偏心度与半径相等的节点
print(nx.center(G))
# 外围节点，偏心度与直径相等的节点
print(nx.periphery(G))

print(nx.density(G))

# 3号节点到图中其它节点的最短距离
node_id = 3
nx.single_source_shortest_path_length(G, node_id)

# 每两个节点之间的最短距离
pathlengths = []
for v in G.nodes():
    spl = nx.single_source_shortest_path_length(G, v)
    for p in spl:
        print('{} --> {} 最短距离 {}'.format(v, p, spl[p]))
        pathlengths.append(spl[p])

# 平均最短距离
print(sum(pathlengths) / len(pathlengths))

# 不同距离的节点对个数
dist = {}
for p in pathlengths:
    if p in dist:
        dist[p] += 1
    else:
        dist[p] = 1
print(dist)

2.5.5 节点特征（重要）

# 可视化辅助函数
def draw(G, pos, measures, measure_name):
    nodes = nx.draw_networkx_nodes(G, pos, node_size=250, cmap=plt.cm.get_cmap('plasma'),
                                   node_color=list(measures.values()),
                                   nodelist=measures.keys())
    nodes.set_norm(mcolors.SymLogNorm(linthresh=0.01, linscale=1))
    # labels = nx.draw_networkx_labels(G, pos)
    edges = nx.draw_networkx_edges(G, pos)

    # plt.figure(figsize=(10,8))
    plt.title(measure_name)
    plt.colorbar(nodes)
    plt.axis('off')
    plt.show()


# 导入无向图
G = nx.karate_club_graph()
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
plt.show()

# 导入有向图
DiG = nx.DiGraph()
DiG.add_edges_from([(2, 3), (3, 2), (4, 1), (4, 2), (5, 2), (5, 4),
                    (5, 6), (6, 2), (6, 5), (7, 2), (7, 5), (8, 2),
                    (8, 5), (9, 2), (9, 5), (10, 5), (11, 5)])
# dpos = {1: [0.1, 0.9], 2: [0.4, 0.8], 3: [0.8, 0.9], 4: [0.15, 0.55],
#         5: [0.5,  0.5], 6: [0.8,  0.5], 7: [0.22, 0.3], 8: [0.30, 0.27],
#         9: [0.38, 0.24], 10: [0.7,  0.3], 11: [0.75, 0.35]}
nx.draw(DiG, pos, with_labels=True)
plt.show()

# Node Degree
print(list(nx.degree(G)))
print(dict(G.degree()))
# 字典按值排序
print(sorted(dict(G.degree()).items(), key=lambda x: x[1], reverse=True))
draw(G, pos, dict(G.degree()), 'Node Degree')

# 节点重要度特征(节点的度，相当于将节点数归一化后的结果) Centrality
# Degree Centrality-无向图
print(nx.degree_centrality(G))
draw(G, pos, nx.degree_centrality(G), 'Degree Centrality')

# Degree Centrality-有向图
print(nx.in_degree_centrality(DiG))
print(nx.out_degree_centrality(DiG))
draw(DiG, pos, nx.in_degree_centrality(DiG), 'DiGraph Degree Centrality')

draw(DiG, pos, nx.out_degree_centrality(DiG), 'DiGraph Degree Centrality')

# Eigenvector Centrality-无向图（特征向量重要度）
print(nx.eigenvector_centrality(G))
draw(G, pos, nx.eigenvector_centrality(G), 'Eigenvector Centrality')

# Eigenvector Centrality-有向图（特征向量重要度）
print(nx.eigenvector_centrality_numpy(DiG))
draw(DiG, pos, nx.eigenvector_centrality_numpy(DiG), 'DiGraph Eigenvector Centrality')

# Betweenness Centrality（必经之地）
print(nx.betweenness_centrality(G))
draw(G, pos, nx.betweenness_centrality(G), 'Betweenness Centrality')

# Closeness Centrality（去哪儿都近）
print(nx.closeness_centrality(G))
draw(G, pos, nx.closeness_centrality(G), 'Closeness Centrality')

# PageRank
print(nx.pagerank(DiG, alpha=0.85))
draw(DiG, pos, nx.pagerank(DiG, alpha=0.85), 'DiGraph PageRank')

# Katz Centrality
print(nx.katz_centrality(G, alpha=0.1, beta=1.0))
draw(G, pos, nx.katz_centrality(G, alpha=0.1, beta=1.0), 'Katz Centrality')
draw(DiG, pos, nx.katz_centrality(DiG, alpha=0.1, beta=1.0), 'DiGraph Katz Centrality')

# HITS Hubs and Authorities
h, a = nx.hits(DiG)
draw(DiG, pos, h, 'DiGraph HITS Hubs')
draw(DiG, pos, a, 'DiGraph HITS Authorities')

# NetworkX文档：社群属性 Clustering
print(nx.draw(G, pos, with_labels=True))

# 三角形个数
print(nx.triangles(G))
print(nx.triangles(G, 0))
draw(G, pos, nx.triangles(G), 'Triangles')

# Clustering Coefficient
print(nx.clustering(G))
print(nx.clustering(G, 0))
draw(G, pos, nx.clustering(G), 'Clustering Coefficient')

# Bridges
# 如果某个连接断掉，会使连通域个数增加，则该连接是bridge。
# bridge连接不属于环的一部分。
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
plt.show()
print(list(nx.bridges(G)))

# Common Neighbors 和 Jaccard Coefficient
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
plt.show()
print(sorted(nx.common_neighbors(G, 0, 4)))
preds = nx.jaccard_coefficient(G, [(0, 1), (2, 3)])
for u, v, p in preds:
    print(f"({u}, {v}) -> {p:.8f}")
for u, v, p in nx.adamic_adar_index(G, [(0, 1), (2, 3)]):
    print(f"({u}, {v}) -> {p:.8f}")

# Katz Index
# 节点u到节点v，路径为k的路径个数。
import numpy as np
from numpy.linalg import inv

G = nx.karate_club_graph()
print(len(G.nodes))
# 计算主特征向量
L = nx.normalized_laplacian_matrix(G)
e = np.linalg.eigvals(L.A)
print('最大特征值', max(e))

# 折减系数
beta = 1 / max(e)

# 创建单位矩阵
I = np.identity(len(G.nodes))

# 计算 Katz Index
S = inv(I - nx.to_numpy_array(G) * beta) - I
print(S.shape)
print(S.shape)

2.5.6 计算全图的Graphlet

# 导入全图
G = nx.karate_club_graph()

plt.figure(figsize=(10,8))
pos = nx.spring_layout(G, seed=123)
nx.draw(G, pos, with_labels=True)

# 指定Graphlet
target = nx.complete_graph(3)
nx.draw(target)
plt.show()

# 匹配Graphlet，统计个数
num = 0
for sub_nodes in itertools.combinations(G.nodes(), len(target.nodes())):  # 遍历全图中，符合graphlet节点个数的所有节点组合
    subg = G.subgraph(sub_nodes)                                          # 从全图中抽取出子图
    if nx.is_connected(subg) and nx.is_isomorphic(subg, target):          # 如果子图是完整连通域，并且符合graphlet特征，输出原图节点编号
        num += 1
        print(subg.edges())

print(num)

2.6.7 拉普拉斯矩阵特征值分解

import numpy.linalg  # 线性代数

# 创建图
n = 1000  # 节点个数
m = 5000  # 连接个数
G = nx.gnm_random_graph(n, m, seed=5040)

# 邻接矩阵（Adjacency Matrix）
A = nx.adjacency_matrix(G)
print(A.shape)
print(A.todense())

# 拉普拉斯矩阵（Laplacian Matrix）
L = nx.laplacian_matrix(G)
print(L.shape)

# 节点degree对角矩阵
D = L + A
print(D.todense())

# 归一化拉普拉斯矩阵（Normalized Laplacian Matrix）
L_n = nx.normalized_laplacian_matrix(G)
print(L_n.shape)
print(L_n.todense())
plt.imshow(L_n.todense())
plt.show()
print(type(L_n))

# 特征值分解
e = np.linalg.eigvals(L_n.A)
print(e)
# 最大特征值
print(max(e))
# 最小特征值
print(min(e))

# 特征值分布直方图
plt.figure(figsize=(12, 8))

plt.hist(e, bins=100)
plt.xlim(0, 2)  # eigenvalues between 0 and 2

plt.title('Eigenvalue Histogram', fontsize=20)
plt.ylabel('Frequency', fontsize=25)
plt.xlabel('Eigenvalue', fontsize=25)
plt.tick_params(labelsize=20)  # 设置坐标文字大小
plt.show()

参考文献

[1] NetworkX 图网络处理工具包

[2] python 工具包 NetworkX 教程翻译

[3] Ego Graph概念介绍

[4] ego network的概念

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/351024.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何修改 类名::静态变量？

如何修改 类名::静态变量？

好久没更新了，其中经历了备战省赛，重装电脑，换服务器，重新搭建博客等一系列事，受到许多技术大牛的指点，而且新人太厉害了，卷卷卷！ Geek Challenge 2021有一道BabyPOP，这…
阅读更多...
vue写一个翻页的时间插件

vue写一个翻页的时间插件

读秒效果有一个从上向下的翻页效果 效果图 clock代码 <template><div class"dateClock"><div class"todayClass"><p class"datep">{{dateToday}}</p><span style"float:right;font-size:16px">…
阅读更多...
基于 VPX 总线的工件台运动控制系统研究与开发-DSP+FPGA硬件架构（一）

基于 VPX 总线的工件台运动控制系统研究与开发-DSP+FPGA硬件架构（一）

作为光刻机核心单元之一&#xff0c;超精密工件台主要负责实现快速扫描、上下片、精密定位、调平调焦等功能。目前&#xff0c;较为成熟的方案大多采用 VME 并行总线架构来建立超精密工件台控制系统&#xff0c;由于随着系统性能要求的提升&#xff0c;VME 总线以及相应的处理器…
阅读更多...
最大连续子列和

最大连续子列和

给定一个数组&#xff0c;求它的最大连续子列和。这个问题有四种解法。 1、暴力循环(O(n^3))分析这个问题&#xff0c;既然是子列&#xff0c;那么它最长为n&#xff0c;最短为1。要想求和我们一般需要知道这个子列的左端下标和右端下标&#xff0c;再求这个子列的和。最简单的…
阅读更多...
深入浅出带你学习Nginx中间件常见漏洞

深入浅出带你学习Nginx中间件常见漏洞

前言 上篇文章总结了APACHE中间件的常见漏洞&#xff0c;本文介绍一个同样很常用的中间件——nginx&#xff0c;本文会讲解关于nginx中间件的常见漏洞利用方式与危害&#xff0c;下面展开来给大家讲解。 Nginx是什么&#xff1f; 在讲漏洞之前我们需要先知道什么是nginx,简单…
阅读更多...
《SQL基础》11. 索引

《SQL基础》11. 索引

SQL - 索引索引概述结构B-TreeBTreeHash思考分类语法SQL性能分析SQL执行频率慢查询日志profile详情explain执行计划索引失效情况范围查询索引列运算字符串不加引号模糊查询or连接条件数据分布影响使用规则最左前缀法则SQL提示覆盖索引前缀索引设计原则索引 概述 索引&#xf…
阅读更多...
linux安装minio，注册服务实现开机自启动

linux安装minio，注册服务实现开机自启动

一、安装1.创建安装目录mkdir -p /usr/local/soft/minio2.下载文件cd /usr/local/soft/miniowget -q http://dl.minio.org.cn/server/minio/release/linux-amd64/minio3.新建数据存储目录mkdir -p /home/minio/data4.授予可执行权限chmod x minio5.设置账号密码export MINIO_AC…
阅读更多...
yolov8代码梳理 训练自己的数据 最终版

yolov8代码梳理 训练自己的数据 最终版

1.总结一下 最开始为了检测不规则的麻包袋&#xff0c;所以采用了目标检测。yolov3&#xff0c;fasterrcnn&#xff0c;ssd。这种矩形框还是可以用。后面检测的物体变成了规则的纸箱&#xff0c;我们还用目标检测发现&#xff0c;没有旋转角度&#xff0c;因为箱子的摆放不是正…
阅读更多...
深度学习算法面试常问问题（三）

深度学习算法面试常问问题（三）

pooling层是如何进行反向传播的&#xff1f; average pooling&#xff1a; 在前向传播中&#xff0c;就是把一个patch的值取平均传递给下一层的一个像素。因此&#xff0c;在反向传播中&#xff0c;就是把某个像素的值平均分成n份 分配给上一层。 max pooling&#xff1a; 在前…
阅读更多...
一文教你如何编写高效的接口测试，别再浪费时间了

一文教你如何编写高效的接口测试，别再浪费时间了

目录 前言 1、什么是接口测试 2、为什么要做接口测试 3、接口测试的范围 4、接口测试的重点 5、测试原则 总结 前言 在所有的开发测试中&#xff0c;接口测试是必不可少的一项。有效且覆盖完整的接口测试&#xff0c;不仅能保障新功能的开发质量&#xff0c;还能让开发在…
阅读更多...
PMP项目管理未来的发展与趋势

PMP项目管理未来的发展与趋势

什么是项目管理&#xff1f;关于项目管理的解释主要是基于国际项目管理三大体系不同的解释及本领域权威专家的解释。 项目管理就是以项目为对象的系统管理方法&#xff0c;通过一个临时性的、专门的柔性组织&#xff0c;对项目进行高效率的计划、组织、指导和控制&#xff0c;以…
阅读更多...
深度学习术语解释:backbone、head、neck，etc

深度学习术语解释:backbone、head、neck，etc

backbone&#xff1a;翻译为主干网络的意思&#xff0c;既然说是主干网络&#xff0c;就代表其是网络的一部分&#xff0c;那么是哪部分呢&#xff1f;这个主干网络大多时候指的是提取特征的网络&#xff0c;其作用就是提取图片中的信息&#xff0c;共后面的网络使用。这些网络…
阅读更多...
深入浅出带你学习利用session.upload_progress进行文件包含

深入浅出带你学习利用session.upload_progress进行文件包含

前言 该思路是很久之前在CTF比赛中学习到的&#xff0c;可以简单理解为利用session.upload_progress来进行文件竞争从而达到上传文件进行文件包含或者命令执行的目的&#xff0c;可能大部分人会不理解&#xff0c;我们下面我们展开来讲。 基础知识 session.upload_progress …
阅读更多...
Java并发编程面试题——线程安全（原子性、可见性、有序性）

Java并发编程面试题——线程安全（原子性、可见性、有序性）

文章目录一、原子性高频问题1.1 Java中如何实现线程安全?1.2 CAS底层实现1.3 CAS的常见问题1.4 四种引用类型 ThreadLocal的问题&#xff1f;二、可见性高频问题2.1 Java的内存模型2.2 保证可见性的方式2.3 volatile修饰引用数据类型2.4 有了MESI协议&#xff0c;为啥还有vol…
阅读更多...
2022年全国职业院校技能大赛网络安全竞赛A模块（2）

2022年全国职业院校技能大赛网络安全竞赛A模块（2）

2022年全国职业院校技能大赛&#xff08;中职组&#xff09; 网络安全竞赛试题 &#xff08;2&#xff09; 目录 2022年全国职业院校技能大赛&#xff08;中职组&#xff09; 网络安全竞赛试题 &#xff08;2&#xff09; 模块A 基础设施设置与安全加固 A-1任务一 登录安…
阅读更多...
ChatGPT引爆资本狂潮，AI大战升级版打响！谷歌紧急上线对标竞品，微软测试AI搜索引擎，百度宣国产版定档，谁才是最后的赢家？

ChatGPT引爆资本狂潮，AI大战升级版打响！谷歌紧急上线对标竞品，微软测试AI搜索引擎，百度宣国产版定档，谁才是最后的赢家？

文 BFT机器人 如果你迄今为止还没有听说过ChatGPT&#xff0c;那就已经彻彻底底被人工智能的新时代甩到身后了。 如果说去年年底ChatGPT刚推出的时候&#xff0c;大多数网友对其的态度还是认为它和Clubhouse一样仅会是昙花一现的话&#xff0c;那么2个月时间过去&#xff0c;C…
阅读更多...
【Ubuntu换源教程】不同Ubuntu系统版本换清华源

【Ubuntu换源教程】不同Ubuntu系统版本换清华源

今天在新电脑上装了虚拟机VMware Workstation Pro 16&#xff0c;在虚拟机上安装了Ubuntu20.04系统。 在做Ubuntu20.04系统换源的时候&#xff0c;发现源要和Ubuntu的版本匹配&#xff0c;之前一直不知道&#xff0c;一直都是盲目换源&#xff0c;版本如果不匹配的话&#xff…
阅读更多...
【日常】矩阵正态分布参数检验问题

【日常】矩阵正态分布参数检验问题

最近给凯爹做的一个苦力活&#xff0c;统计检验这个东西说实话也挺有趣&#xff0c;跟算法设计一样&#xff0c;好的检验真的是挺难设计的&#xff0c;就有近似算法的那种感觉&#xff0c;检验很难保证size和power都很理想&#xff0c;所以就要做tradeoff&#xff0c;感觉这个假…
阅读更多...
DPR-34 AC22V【双位置继电器】

DPR-34 AC22V【双位置继电器】

系列型号&#xff1a; DPR-20双位置继电器&#xff1b;DPR-31双位置继电器&#xff1b; DPR-32双位置继电器&#xff1b;DPR-33双位置继电器&#xff1b; DPR-34双位置继电器&#xff1b;DPR-35双位置继电器&#xff1b; DPR-11双位置继电器&#xff1b;DPR-12双位置继电器&…
阅读更多...
Python-项目实战--贪吃蛇小游戏-游戏框架搭建（3）

Python-项目实战--贪吃蛇小游戏-游戏框架搭建（3）

1.游戏框架搭建介绍pygame开发图像界面游戏的几个要素&#xff0c;并且把贪吃蛇游戏的整体框架搭建完成本节知识点包括&#xff1a;pygame的初始化和退出游戏主窗口游戏循环和游戏时钟主窗口背景颜色绘制文本pygame的坐标系游戏事件监听绘制图形定时器事件1.5绘制文本pygame的f…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023