给定一个数组,求它的最大连续子列和。
这个问题有四种解法。
1、暴力循环(O(n^3))
分析这个问题,既然是子列,那么它最长为n,最短为1。要想求和我们一般需要知道这个子列的左端下标和右端下标,再求这个子列的和。最简单的办法就是用暴力循环来求和。
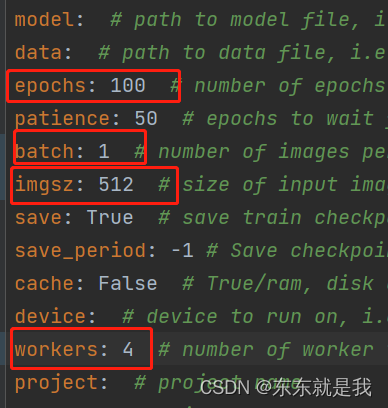
首先我们需要定义左端下标i,每次循环i++。接下来是右端下标j,j的初值为i,因为右端下标总是大于等于左端下标,每次循环j++。知道了左端下标i和右端下标j之后,再从i到j循环求和就行了。
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1*10^6;
int main()
{
int n;
cin>>n;
int a[N];
int sum=0,maxsum=0;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n;i++)
{
for(int j=i;j<n;j++)
{
sum=0;
for(int k=i;k<=j;k++) sum+=a[k];
if(sum>maxsum) maxsum=sum;
}
}
cout<<maxsum;
return 0;
} 2、暴力循环的改进(O(n^2))
第一种算法显然时间复杂度太高了,可以进行改进,减少一层循环。
当左端下标i和右端下标j确定时,知道a[i]~a[j]的和,如果要求a[i]~a[j+1],按照第一种算法,需要重新遍历一遍a[i]~a[j]的数组,再把a[j+1]加上。思考后,我们发现,如果已知a[i]~a[j]的和sum,我们只需要让sum+a[j+1]就可以得到a[i]~a[[j+1]的和。因此我们就可以使用两层循环就可以解决这个问题。
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1*10^6;
int main()
{
int n;
cin>>n;
int a[N];
int sum=0,maxsum=0;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n;i++)
{
sum=0;
for(int j=i;j<n;j++)
{
sum+=a[j];
if(sum>maxsum) maxsum=sum;
}
}
cout<<maxsum;
return 0;
}值得注意的是,第一个算法中sum重置为0是在第二个循环里,第二个sum重置为0是在第一层循环里。原因是第一个算法的第三层循环是循环累加求值,所以每次循环前要重置为0,而第二个算法简化后,左端i确定后,利用累加的方法记录以左端i为首长度为1~n-i+1的各子列的和,所以在第一重循环确定新的左端i后,就要重置sum。
3、分治(O(n*logn))
当我们看到一个算法的时间复杂度是O(n^2)的时候,我们就可以思考这个算法能不能经过改进将时间复杂度降为O(n*logn)
这个问题也可以用分治的方法来解决。(有时候想想这些算法题真操蛋,万物可分治可二分可递归了^_^)
分治是将大的问题划分成小的问题,最后整合结果的方法。分是划分,治是整合结果。
怎么分治呢?我们考虑到,把整个数列从中间切开,最大子列和=max(左边数列最大子列和,右边数列子列和,跨越边界的子列和),跨越边界的子列和就是左右两边的数都包含的情况。利用这个办法,不断地将子列切片,进行分治,最终就能求得整个数列的最大子列和。
代码有点复杂,回头有空再写吧^_^4、在线处理!(O(n))!
这是对于最大子列和最好最快的算法。
这个算法的思想是,从左到右累加每个数得到sum,如果sum>maxsum,更新maxsum=sum,如果sum<0,将sum重置为0。输出最后的sum值。
为什么这个算法是正确的呢?如果任意一个子列和小于0,那么这个子列一定不会位于和最大子列的左侧,因为一个负数对于整个数列的和是没有贡献的。
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1*10^6;
int main()
{
int n;
cin>>n;
int a[N];
int sum=0,maxsum=-1*10^6;
for(int i=0;i<n;i++)
{
cin>>a[i];
sum+=a[i];
if(sum<0) sum=0;
if(sum>maxsum) maxsum=sum;
}
cout<<maxsum;
return 0;
}为什么,我把maxsum设为负数呢,因为有的算法题给的数据实在变态,你必须考虑符合题意的每一种极端情况。把maxusm设置为负数,我是考虑到,只有一个元素且为负数的情况。
为什么它叫在线处理呢?因为它可以边输入边计算,只需要一个循环。而算法复杂度只能这么小了,毕竟输入数据的算法也需要O(n)。
这四种算法思想均来自中国大学mooc陈越老师的数据结构课。
md,真爽,还有啥比ac更爽的?!纠结这么久终于找到bug,解决这道题了。