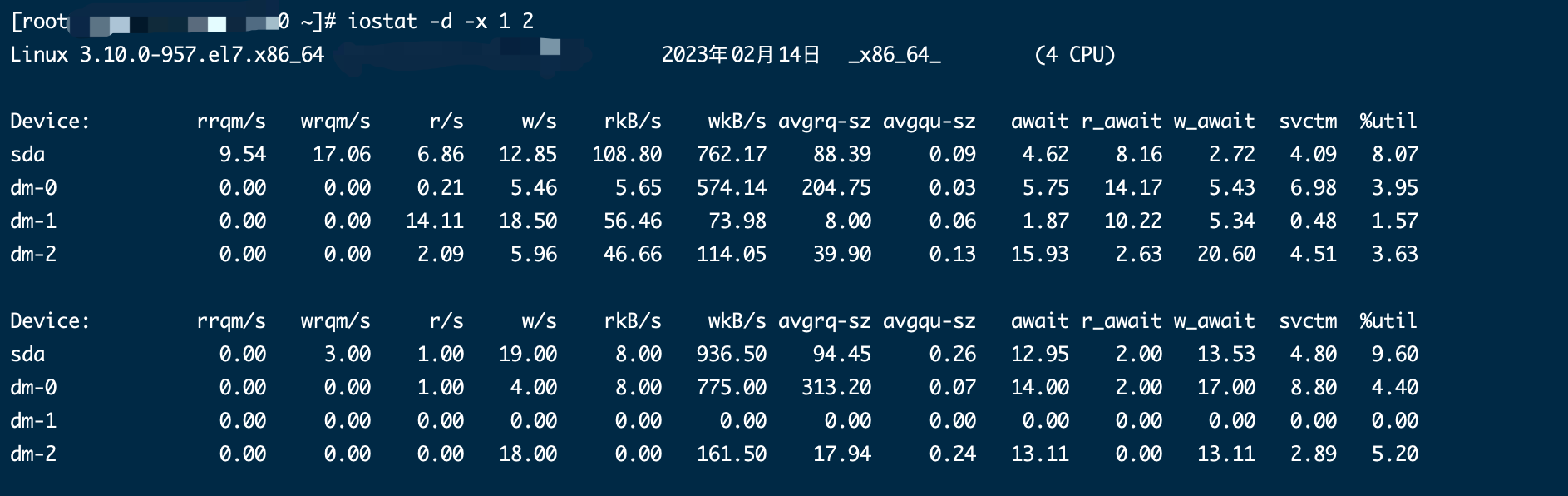
文章目录
- 一、递推的概念
- 二、递推和递归的区别
- 三、递推的实例
- 1、最基础的:斐波那契数列
- 2、变形版斐波那契数列
- 3、较复杂的递推式求解:昆虫繁殖
- 4、经典逆推问题:题目数量
一、递推的概念
1、什么是递推算法?
递推算法:是指从已知的初始条件出发,依据某种递推关系,逐次推出所要求的各中间结果及最后结果。
简单来说,就是你今天的成果是和昨天以及前天的努力有关系的
2、解决递推问题的一般形式
(1)建立递推关系式;
(2)确定边界条件(即初始值);
(3)递推求解。
二、递推和递归的区别
1、从程序上看,递归表现为自己调用自己,递推则没有这样的形式。
2、递归是从问题的最终目标出发,逐渐将复杂问题化为简单问题,最终求得问题 是逆向的。递推是从简单问题出发,一步步的向前发展,最终求得问题。是正向的。
3、递归中,问题的n要求是计算之前就知道的,而递推可以在计算中确定,不要求计算前就知道n。
三、递推的实例
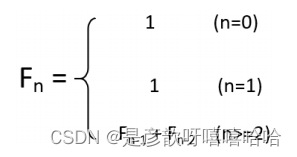
1、最基础的:斐波那契数列
问题描述:Fibonacci 数列的代表问题是由意大利著名数学家 Fibonacci 于 1202年提出的“兔子繁殖问题” (又称“Fibonacci 问题”)引出的。一个数列的第 0 项为 1,第 1 项为 1,以后每一项都是前两项的和,这个数列就是著名的斐波那契数列,求斐波那契数列的第 N 项。由问题,可写出如下所示递推方程:
#include<iostream>
using namespace std;
int main() {
int a[1000],n;
cin>>n;
a[0]=a[1]=1;
for(int i=2;i<=n;i++) {
a[i]=a[i-1]+a[i-2];//递推式
}
cout<<a[n];
return 0;
}
2、变形版斐波那契数列
有一组序列的数值是:1、2、9、33、126、477…请同学们认真观察数值的规律。现要求:指定项数为任意的可项,计算:
1)第 N项的数据:
2)输出前N项数据的和
输入:只有一行,包含1个整数(其中 3<=N<=15)为这个序列的项数。
输出:两行。
第一行为这个序列第N项的数据。
第二行为这个序列前N项的数据和。
[样例输入]6
[样例输出]477
648
解题思路:前两项和的3倍是第三项
#include<iostream>
using namespace std;
int main() {
int a[50]={0},n,sum=0;
cin >> n;
a[1]=1;//从下标为1开始,所以最后输出的结果是a[n]
for(int i=3;i<=n;i++) a[i]=(a[i-1]+a[i-2])*3;//递推式
for(int i=1;i<=n;i++) sum+=a[i];//求前N项和
cout<<a[n]<<endl<<sum;
return 0;
}
3、较复杂的递推式求解:昆虫繁殖
问题描述: 科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过 X 个月产 Y 对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过 X 个月产卵),问过 Z 个月以后,共有成虫多少对?
【输入格式】输入 X,Y,Z 的数值(0=<X<=20,1<=Y<=20,X=<Z<=50)。
【输出格式】输出过 Z 个月以后,共有成虫对数
样例输入:1 2 8
样例输出:37
一定要找出递推公式
算法分析:本月成虫数量 = 上月成虫数量 + 两个月前新增卵的数量新增卵的数量 = 上月成虫数量 * 2(Y 的值)

#include <iostream>
using namespace std;
int main(){
long long a[101] = {0}, b[101] = {0};
int x, y, z;
cin >> x >> y >> z;
for(int i =1; i <= x; i++){
a[i] = 1;
b[i] = 0;
}
for(int i= x + 1; i <= z + 1; i++){
b[i] = y * a[i-x];//重点在这里
a[i] = a[i-1] + b[i-2];//重点在这里
}
cout << a[z+1] << endl;
return 0;
}
4、经典逆推问题:题目数量
问题描述:N 名同学争做计算题,规定做完一道才能做第二道,比赛后统计发现:第一位同学做了总数的一半多 1 道,第二位同学做了余下的一半多 2 道,第三位同学做了再余下的一半多 3 道,以此类推,第 N-1 位同学做了余下的一半多 N-1道,最后一位同学做了 N 道。输入学生的数量 N,求共有多少道题目?
样例输入:4
样例输出:66
算法分析:
第 n 名学生做题时还剩题目数量为:N
第 n-1 名学生做题时还剩题目数量为: (N+N-1)*2
第 N-2 名学生做题时还剩题目数量为:((N+N-1)*2+N-2)*2
……
通过以上分析,可以发现:
边界条件为 F1=N
递推关系式为 Fn-1=(Fn+N-1)*2
#include <iostream>
using namespace std;
int main(){
int n, f[101]={0};
cin >> n;
f[n]=n;
while(n>=0){
f[n-1]=(f[n]+n-1)*2;
n--;
}
cout << f[1];
return 0;
}